以下で、三角形の頂点からの距離の積の公式(その2)と、三角形の中線の長さの公式との関係を整理します。
【中線の長さの公式(中線定理)】
上図のように、三角形ABCの辺BCの中点Mと頂点Aを結んだ中線AMの長さmに関して、上の式1が成り立つ。式1は式2の形に書き変えて使うことができる。
この公式の証明は、ここをクリックした先のページにあります。
この中線の長さの公式(中線定理)以外の以下の公式は、中線定理に比べて覚えにくいように思います。
そのため、以下の公式は高校入試問題にはほとんど出ないようにも考えられます。
しかし、図形の難問を解く受験の戦いで、使える道具は多い方が安心ですので、それらも覚えてみてください。
【頂点からの距離の積の公式】
上式のように、三角形ABCの頂点Cから辺ABへ垂直に引いた線との交点Hに関する線分の積が以下の式であらわされる。
AH×AB=m2-s2
この公式の証明は、ここをクリックした先のページにあります。
一方、中点の長さの公式は:
(b2+c2)/2=m2+s2
である。
これらから、AHが以下の通り計算できる。
三角形の頂点Cの辺AB上への足Hまでの長さAH
がこの式であらわされることは、
以下の公式でもあった。
【三角形の頂点の足の位置の公式】
上図の三角形ABCの頂点Aの左右へのずれを計算する上の式が成り立つ。
この公式の証明はここをクリックした先のページにあります。
この式を使うと頂点Aの辺BC上への足Dと点Bの間の長さBDが計算できる。
この公式のポイントと、三角形の頂点からの距離の積の公式のポイントとの関係を、以下の図で整理して覚えてください。
上の図は、下の図をいっしょに覚えると覚え易いです。
この図から、以下の関係が成り立っている事も思い出せます。
リンク:
中学数学の目次
【中線の長さの公式(中線定理)】
上図のように、三角形ABCの辺BCの中点Mと頂点Aを結んだ中線AMの長さmに関して、上の式1が成り立つ。式1は式2の形に書き変えて使うことができる。
この公式の証明は、ここをクリックした先のページにあります。
この中線の長さの公式(中線定理)以外の以下の公式は、中線定理に比べて覚えにくいように思います。
そのため、以下の公式は高校入試問題にはほとんど出ないようにも考えられます。
しかし、図形の難問を解く受験の戦いで、使える道具は多い方が安心ですので、それらも覚えてみてください。
【頂点からの距離の積の公式】
AH×AB=m2-s2
この公式の証明は、ここをクリックした先のページにあります。
一方、中点の長さの公式は:
(b2+c2)/2=m2+s2
である。
これらから、AHが以下の通り計算できる。
がこの式であらわされることは、
以下の公式でもあった。
【三角形の頂点の足の位置の公式】
上図の三角形ABCの頂点Aの左右へのずれを計算する上の式が成り立つ。
この公式の証明はここをクリックした先のページにあります。
この式を使うと頂点Aの辺BC上への足Dと点Bの間の長さBDが計算できる。
この公式のポイントと、三角形の頂点からの距離の積の公式のポイントとの関係を、以下の図で整理して覚えてください。
リンク:
中学数学の目次






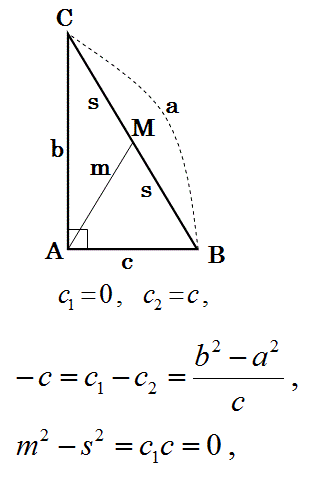

0 件のコメント:
コメントを投稿