余弦定理の確実な思い出し方

以下の様にすれば、余弦定理を確実に思い出すことができると思います。

　上図の直角三角形を思い浮かべ、上の余弦定理の式を連想して思い出すようにしましょう。
　直角三角形の２辺の二乗の差は、「三角形の辺の二乗の引き算の公式」により、下図の様に、関係する三角形の２辺の二乗の差と同じになることを、以下の式を連想して素早く証明できるようになりましょう。

（余弦定理の導出おわり）

（別の導出方法）
「三角形の辺の二乗の引き算の公式」の以下の式１を使う。

（余弦定理導出おわり）

【三角形の辺の二乗の引き算の公式から余弦定理を思い出す】
 （三角形の辺の二乗の引き算の公式は覚え易い）
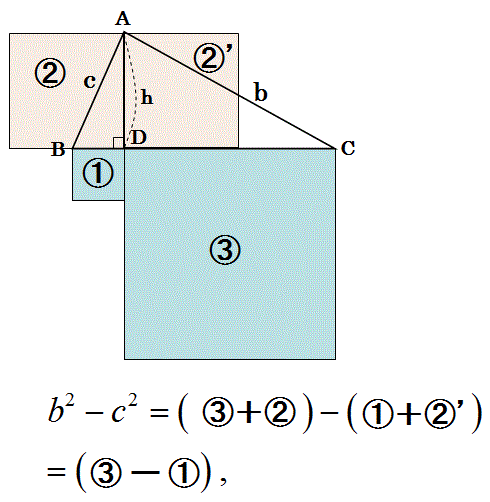
　三角形の辺の二乗の引き算の公式は、以下の図の正方形①②③を心が思い描いて心が公式を導き出すので、覚え易い（導き出し易い）です。

【三角形の辺の二乗の引き算の公式】

 （以上が、三角形の辺の二乗の引き算の公式）

　上の式の三角形の辺の二乗の引き算の公式を思い出して、次に、その公式を変形して余弦定理を速やかに導き出したら良いと考えます。

（以上が、余弦定理）

　また、三角形の辺の二乗の引き算の公式を覚えて使うと余弦定理が楽に導けるので、余弦定理を使って解くべき問題は、三角形の辺の二乗の引き算の公式を使えば解けるのではないかと考えられます。
　実際、余弦定理を使って解いている問題は、ことごとく、三角形の辺の二乗に引き算の公式を使って解けます。三角形の辺の二乗の引き算の公式には、三角形の２辺の１辺への射影の長さの関係を表わす、射影の基本的特徴を利用できるようにする特徴があります。その特徴が、余弦定理と共通する、射影を利用して問題を解き易くする特徴だと考えています。（射影を利用するこの特徴は、ベクトルの内積の計算とも共通した特徴です。）
　むしろ、三角形の辺の二乗の引き算の公式の方が余弦定理よりも、問題を解くために使い易い公式だと思う。
　そのため、三角形の辺の二乗の引き算の公式を覚えていれば、余弦定理を覚えていなくても、問題を解くのに支障がありません。そういう意味で、三角形の辺の二乗の引き算の公式を覚えていれば、余弦定理を覚え無いでも良い事がわかりました。
　そもそも、三角形の辺の二乗の引き算の公式をあらわす式と、余弦定理をあらわす式は、式の１つの変形だけで結び付いている等価な式です。両者は、式を変形して形を変えただけの同じ式だと言って良いと思います。

　余弦定理を思い出す毎に、以下のように、「２項の積の二乗の差への変換」の公式を使って、三角形の辺の二乗の引き算の公式に変換できる事を確認することで、思い出した記憶に間違いが無い事を確認してください。

（結論）
　余弦定理も、余弦定理を使って導き出すその他の定理も、等しく、三角形の辺の二乗の引き算の公式を使って導き出すようにしましょう。

リンク：
ベクトルによる三角形の余弦定理のやさしい覚え方
高校数学の目次