【問1】以下の式が成り立つ事を証明せよ。
【解説】
「右辺を微分したら左辺の被積分関数になるから、証明終わり。」
という証明でも良いです。
しかし、この積分の公式には、以下のような味わい深い意味がありますので、
その意味を味わいながら、左辺から、じっくりと、右辺を導き出しましょう。
先ず、以下の関数と、その逆関数の組がある事を覚えてください。
sinh(x)という関数は、

という式で定義されます。
これらの関数のグラフを描くと以下の図になります。
これらの関数の組で、逆関数が上の式になる事は、各自で計算して確認しておいて下さい。
【第1の積分の解1】
(証明おわり)
【第1の積分の解2】
「変数変換して無理関数の根号を外す公式」を参考にし:


(証明おわり)
【第1の積分の解3】
以下の様にして証明することもできます。
(証明おわり)
【第2の積分の解1】
x>1,

(証明おわり)
【第2の積分の解2】
「変数変換して無理関数の根号を外す公式」を使い(xが正の場合も負の場合の解もまとめて以下の計算で求めます):


(証明おわり)
(補足) この導き方では、|u|<|x|なので、x<0ならばt<0になり、また、x>0ならばt>0である事も容易にわかる。また、t<0であっても、uの式が、u≧0であるために、0>t≧−1である。
【第2の積分の解3】
第2の積分は、
「不定積分の不思議な解き方」
の解の形を覚えておいて、その解をtと置いた置換積分で解を求めても良い。
x>1の積分区間では:
が得られ、
x<-1の積分区間では:
が得られる。
(第2の積分の解3おわり)
この解3は覚えやすい形をしているので覚えておいた方が良いと思う。
(解2からこの解3を発想するのは、意識していなければとても難しい事だと思う)
【第2の積分の解4】
第2の積分を、x≧1とx≦-1との場合を合わせて、以下の変数に置き換える置換積分で解いてみます。


(場合1) 先ず、x>1の場合を解きます。

この関数のx→1での極限値をx=1での値とする:

この関数のx→1の極限値をx=1での値とする。その結果、x≧1での、以下の積分結果が得られた。

(場合2) 次に、x<-1の場合を解きます。


この関数のx→-1の極限値をx=-1での値とする。その結果、x≦-1での、以下の積分結果が得られた。

この関数の式は、x≧1の場合の積分結果と同じ形をしている。しかし、この関数の定義域はx≦-1であるので、定義域がx≧1であった先の関数とは異なる関数である。
(第2の積分の解4おわり)
この解4の変数変換による方法は、式が複雑になって計算ミスが多くなる難点がある。
【問2】以下の関数の逆関数を求めよ。

【解答】
x≧0のときy≧0,
x≦0のときy≦0,
(解答おわり)
【問3】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【解答】
(ただし、y≧0)
(解答おわり)
【問4】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【解答】
よって、y≦0
(解答おわり)
【問5】以下の積分をせよ。

【解答】

先の公式を使う。

(解答おわり)
リンク:
高校数学の目次
【解説】
「右辺を微分したら左辺の被積分関数になるから、証明終わり。」
という証明でも良いです。
しかし、この積分の公式には、以下のような味わい深い意味がありますので、
その意味を味わいながら、左辺から、じっくりと、右辺を導き出しましょう。
先ず、以下の関数と、その逆関数の組がある事を覚えてください。
sinh(x)という関数は、

という式で定義されます。
これらの関数のグラフを描くと以下の図になります。
これらの関数の組で、逆関数が上の式になる事は、各自で計算して確認しておいて下さい。
【第1の積分の解1】
(証明おわり)
【第1の積分の解2】
「変数変換して無理関数の根号を外す公式」を参考にし:


(証明おわり)
【第1の積分の解3】
以下の様にして証明することもできます。
(証明おわり)
【第2の積分の解1】
x>1,

(証明おわり)
【第2の積分の解2】
「変数変換して無理関数の根号を外す公式」を使い(xが正の場合も負の場合の解もまとめて以下の計算で求めます):


(証明おわり)
(補足) この導き方では、|u|<|x|なので、x<0ならばt<0になり、また、x>0ならばt>0である事も容易にわかる。また、t<0であっても、uの式が、u≧0であるために、0>t≧−1である。
【第2の積分の解3】
第2の積分は、
「不定積分の不思議な解き方」
の解の形を覚えておいて、その解をtと置いた置換積分で解を求めても良い。
x>1の積分区間では:
が得られ、
x<-1の積分区間では:
が得られる。
(第2の積分の解3おわり)
この解3は覚えやすい形をしているので覚えておいた方が良いと思う。
(解2からこの解3を発想するのは、意識していなければとても難しい事だと思う)
【第2の積分の解4】
第2の積分を、x≧1とx≦-1との場合を合わせて、以下の変数に置き換える置換積分で解いてみます。


(場合1) 先ず、x>1の場合を解きます。

この関数のx→1での極限値をx=1での値とする:

この関数のx→1の極限値をx=1での値とする。その結果、x≧1での、以下の積分結果が得られた。

(場合2) 次に、x<-1の場合を解きます。


この関数のx→-1の極限値をx=-1での値とする。その結果、x≦-1での、以下の積分結果が得られた。

この関数の式は、x≧1の場合の積分結果と同じ形をしている。しかし、この関数の定義域はx≦-1であるので、定義域がx≧1であった先の関数とは異なる関数である。
(第2の積分の解4おわり)
この解4の変数変換による方法は、式が複雑になって計算ミスが多くなる難点がある。
【問2】以下の関数の逆関数を求めよ。

【解答】
x≧0のときy≧0,
x≦0のときy≦0,
(解答おわり)
【問3】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【解答】
(ただし、y≧0)
(解答おわり)
【問4】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【解答】
よって、y≦0
(解答おわり)
【問5】以下の積分をせよ。

【解答】

先の公式を使う。

(解答おわり)
リンク:
高校数学の目次






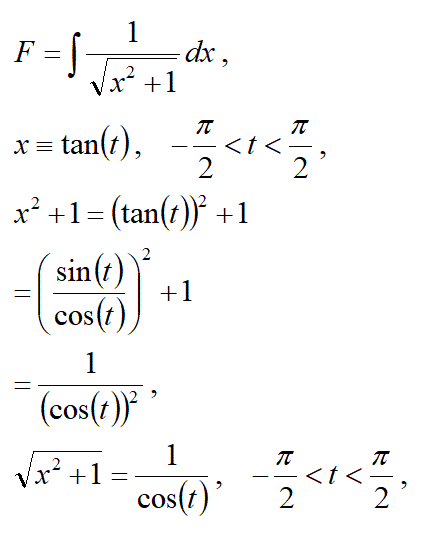





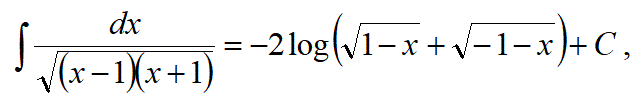

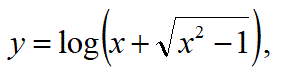


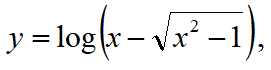


0 件のコメント:
コメントを投稿