【共役複素数を使ってグラフを解析する方法に関する本質的な問題点】
共役複素数を使ってグラフを表現する方法では、以下の双曲線のグラフを変換した場合のグラフの形がどういう形になるかを解析することができません。
要するに、グラフを複素数zとその共役な複素数で表した場合、そのグラフの形が理解できるのは、答えのグラフが、直線か円かの、よく知られた形のみに限定されます。
自分の知らないグラフに対しては新しい情報を得ることができないという、有用性が限定された手法です。
【複素数平面のグラフの変換には媒介変数を使うべし】
そのため、複素数平面の変換には、この様に制約されないため、媒介変数を使ってグラフを変換するべきです。
双曲線の座標zは、媒介変数θを使って以下の式で表せます。
(式2で双曲線があらわせます)
この複素数zを
ω=1/z
で変換したグラフは、以下の式で表せます。
(変換結果の式)
cos(2θ)が負になるθの値では、グラフがあらわせませんが、その場合には双曲線でもグラフが表せていませんでしたので、双曲線と事情が同じです。
リンク:
高校数学の目次
共役複素数を使ってグラフを表現する方法では、以下の双曲線のグラフを変換した場合のグラフの形がどういう形になるかを解析することができません。
要するに、グラフを複素数zとその共役な複素数で表した場合、そのグラフの形が理解できるのは、答えのグラフが、直線か円かの、よく知られた形のみに限定されます。
自分の知らないグラフに対しては新しい情報を得ることができないという、有用性が限定された手法です。
【複素数平面のグラフの変換には媒介変数を使うべし】
そのため、複素数平面の変換には、この様に制約されないため、媒介変数を使ってグラフを変換するべきです。
双曲線の座標zは、媒介変数θを使って以下の式で表せます。
(式2で双曲線があらわせます)
この複素数zを
ω=1/z
で変換したグラフは、以下の式で表せます。
cos(2θ)が負になるθの値では、グラフがあらわせませんが、その場合には双曲線でもグラフが表せていませんでしたので、双曲線と事情が同じです。
リンク:
高校数学の目次


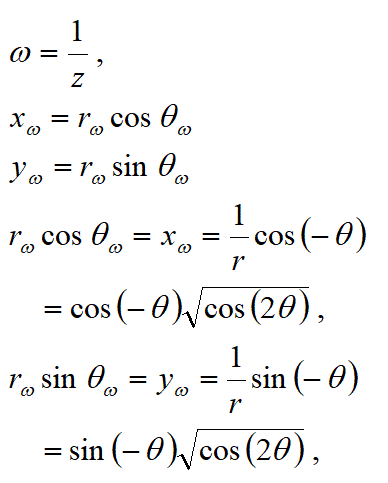
0 件のコメント:
コメントを投稿