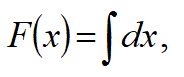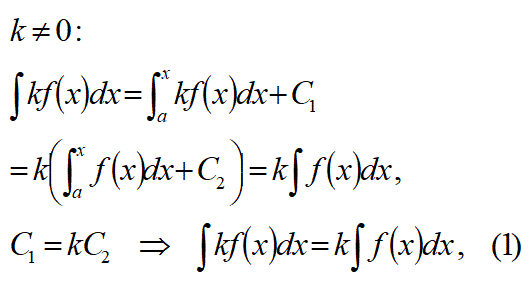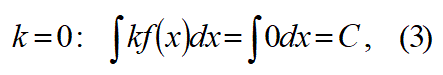【純粋な不定積分】
という式で定義された関数S(x)が純粋な不定積分であって、1つながりのグラフになります。
この積分の起点の値aを変えるとS(x)の値が変わるので、S(x)には、積分定数Cで表せる任意性があります。
不定積分の詳しい説明は、ここをクリックした先のページを参照してください。
【定義を拡大した不定積分】__任意の積分定数を加える__
被積分関数f(x)が:
f(x)=0
という場合を考えます。
この関数f(x)を、
f(x)が定義されている区間における、
a≦x≦b
の範囲のxまで積分します。
積分結果の関数S(x)の値が、積分の起点のaの値を変えた場合にどうなるかを調べてみます。
すると、常に、
となってしまい、この計算で得た不定積分は、aを変えても値が変わらず、積分定数Cの値が任意の値にまで変化しません。
そういう事があるので、不定積分S(x)を、微分するとf(x)になる全ての関数F(x)にまで、定義を拡大します。
すなわち、不定積分F(x)を、
と定義し、
純粋な不定積分S(x)に任意の積分定数Cを加えた関数F(x)にまで不定積分の定義を拡大します。
ただし、積分定数Cは、どの数値でも良いが、ある固定した値をCという記号であらわしているに過ぎないものです。
すなわち、積分定数Cは、関数F(x)に、普通の関数とは異なる正体不明な不定性という性質を帯びさせるというものでもありません。定数Cはありふれた1つの定数に過ぎないものです。
ただし、ある不定積分の式の積分定数Cとして、ある1つの定数を選んだ場合、その定数Cの値は、その不定積分の式を使った一連の計算の中で、一貫して、同じ値にしなければなりません。計算の途中でCの値を変えてはいけないのです。
すなわち、計算の途中のどこに出て来る不定積分同士の間でも、
を成り立たせなければなりません。
それは、(同じ履歴の)値 0 の不定積分の場合でも、
を成り立たせます。
(ただし、履歴の異なる2種類の、値 0 の不定積分がある場合は、それらの異なる2種類の関数を区別して考えなければならない。)
履歴の異なる2種類の不定積分(被積分関数f(x)は同じ)については、それらの不定積分が異なる関数なので、異なる式で記述したいです。しかし、不定積分の表し方は、同じ式の ∫f(x)dx としか表せないので、その履歴を区別する事が困難です。これは悩ましい問題です。
純粋な不定積分であれば、この様なあいまいさに由来する問題はありません。
定義を拡大した不定積分では積分定数Cの定義が拡大されていますが、
不定積分の正しい計算は、定義を拡大した不定積分であっても、純粋な不定積分:
の計算に反しない計算が正しい計算であると考えます。
不定積分の定義を拡大した副作用として生じた以下の誤りに陥らないように注意する必要があると思います。
不定積分同士の引き算:
というふうにして、F(x)-F(x)=Cとして解く解き方がしばしば使われています。
しかし、それは、誤った解き方だと考えます。
値0の不定積分は:
というふうに、積分定数Cを使って定義されます。
しかし、同じ2つの不定積分の引き算の場合には、値0の不定積分を使う必然性も無く、また、同じ不定積分で一貫して同じ値の積分定数がキャンセルされて無くなってしまうので、値が0になります。

となります。
一方で、
が成り立つため、不定積分同士の引き算の式に、どうしても0の不定積分を導入しなければならない場合は:
と計算しなければならないと考えます。
(同じ履歴の関数同士の場合の)値 0 の不定積分でも:
とします。
間違った計算:
の具体例として、
例えば、以下の例の様に、積分定数Cの値を具体化すれば、
の2つの関数を考えることができます。
不定積分の関数F(x)を1つ定義したときには、そのうちの1つのみが選択されなければなりません。
しかし、そうせずに、不定積分を、
とあらわしてあいまいにしてから、
F(x)の積分定数を一貫させずに、
という計算をしてはいけない。
という誤った不定積分の引き算の計算は、そういう誤った計算をしている。
そのような誤りを犯さずに、
F(x)-F(x)=0として解く解き方が、正しい解き方であると考えます。

となるように、不定積分は、一貫して同じ不定積分のみを使って計算するのが正しい解き方であると考えます。
(しかし、∫0dx の場合は、一貫して同じ不定積分のみを記述するというルールで縛る事ができず、頻繁に異なる履歴の不定積分が出現してしまう、悩ましい問題があります。)
誤った計算をして、同じ履歴の不定積分同士の引き算を、
F(x)-F(x)=C
としてしまい、
その式を変形して、
0=C,かつ,C≠0
とするような矛盾を持ち込むべきでは無いと考えます。
そのため、以下の様な計算は間違っていると考えます。
不定積分は、定数を無限に増殖させる正体不明な関数というものでは無いので、上の式の様に定数が生み出されるという事はありません。
また、「上の式4’の左辺の不定積分は、右辺では任意性のある積分定数Cを含む式であらわされるべきだから、この式4’の右辺に積分定数Cを加える」というのも、
本末転倒な議論です。
右辺に積分定数Cが無い式4’が得られた時点で、
どこかで計算の間違いを犯したと判断するべきです。
その計算間違いを、答えの形をつくろう事でごまかすべきでは無いと考えます。そうならないように、先行する式から、以下で説明する、(推奨される式)を書いておいて備えておくべきと考えます。
【推奨される式の記述】
複数の(定義を拡大した)不定積分の加減算を行う場合は特に慎重に行う必要があります。
という計算を行わなければならない場合も生じ得るからです。
この問題に対応するには、不定積分の加減算の計算の式の最後には必ず積分定数Cを加えるようにしなければならないとも考えます。
すなわち、以下の式の様に、式の右辺に積分定数Cを加えて書くのが望ましいと考えます。
(推奨される式) 後の式(6)
ただし、演算の筋が通らない:
という式を書いてはいけない。
また、積分の変換をした直後等の、タイミングの良い式から、推奨される式の形で積分定数Cを混ぜるべきです。
(注意)1つの式の中に不定積分が複数あれば、積分定数が不定積分の中に吸収されて調整するから積分定数を省略して良いと教わったかもしれません。例えば、部分積分法が、積分定数Cを省略した形で教えられています。
しかし、それは誤りです。
不定積分を部分積分で計算するときには、以下に示す、正確な部分積分の公式を使わなければなりません。

(注意)この式1が正しい部分積分の公式ですが、普通は部分積分の公式に付随する第1の積分定数Cは省略して書かない(この第1の積分定数Cは、残った不定積分の項を積分したときに出て来る第2の積分定数Cとは異なるものです)。しかし、問題を正しく解くためには、この公式の第1の積分定数Cを省略できない。
その式の中のある項の不定積分が他の項の不定積分と同じ式であるという紐付きの不定積分の式があります。そういう場合には、その紐付きの不定積は、積分定数を吸収して調整する事が出来ません。そういうときには、(例えば部分積分の公式で)式の中に書くべき積分定数を省略してはいけません。
【怪しい公式】
式1が成り立つと教わって来たと思います。しかし、以下に説明するように、この式1の根拠は怪しいと考えます。
k=0の場合には:
この場合に、式1と同様な式2が成り立つでしょうか。
しかし、
「式2にはならず、以下の式3が成り立つ」
と教わったと思います。
もし、式3になるならば、同様にして、以下の式4にもなるハズです。
(ただし、|k|≠1)
実際、以下の計算で式4が導き出されます。
(|k|=1の場合は、式4の積分定数Cは0になります)
そして、式4の方が式1よりも正しい式であると考えます。
なぜなら、式3も式4も、
(推奨される式) 後の式(6)
と同じ形の式だからです。
推奨される式と同じ形の式3と式4が成り立ち、
式1の根拠は無いと考えるのが正しいと思います。
そもそも、式1の形の公式は、大学で学ぶ正しい微分積分では、定積分の公式、又は、純粋な不定積分の公式として学ぶ公式であって、定義を拡大した不定積分に対して成り立つ公式では無いのです。
(正しい公式)
です。式4の、k=0の場合が式3です。
また、式3' では、値 0 の不定積分であっても、
が成り立ちます。
しかし、値 0 の積分は、
(同じ履歴の)値 0 の不定積分の場合は、
が成り立たちますが、
履歴が異なる値 0 の不定積分も同じ積分記号で表現されていて区別できない問題があります。
(履歴が異なる)値 0 の不定積分の場合は、
となってしまう問題があります。
計算の履歴が分からない、値 0 の不定積分同士の差は、上の式の様に、0とならない場合もあり得る積分定数Cであらわさざるを得ないという問題があります。
(不定積分が同じ履歴か否かは、その不定積分が導き出される演算過程を見ることで判別できます。)
同じ履歴の不定積分同士の関係であって、明らかに等号が成り立つ、|k|=1の場合の式5や、式7や、
式全体に0を掛け算して明らかに0になる式、
以外では、いずれの不定積分の演算にも積分定数Cの不定性が入り込むと考えるのが良いと考えます。
また、その様に注意深く積分定数を入れた式を使って計算しないと、明らかに成り立つ式7に対して、積分定数Cが加わった以下の式が得られてしまい、
同じ履歴の不定積分の2つの項の引き算の結果を0にすると:
0=C and C≠0,
という式になる。
という矛盾に導かれてしまいます。
高校数学の微分積分の教えでは、
不定積分の演算では、
0=C and C≠0,
が導き出されるのが当たり前である、
と教えられている様です。
そのようになるため、不定積分の項同士を引き算する正しい演算はしてはいけない演算であると教えられている様です。
それを教わった高校生は、「正しい演算規則であっても、それを使っていけない場合がある。正しい演算規則とは何?」と考え、微分積分が分からなくなるだろうと考えます。
2つの不定積分の項を引き算して 0 にしてはいけない場合は、同じ形に表現された2つの不定積分が異なる履歴を持つ場合です。
(関数の履歴を考える煩わしさからの開放)
不定積分の履歴が同じか、異なるか、履歴を気にせず計算するには、計算の中に新たな不定積分を導入する都度:
で積分定数Cを定義した関数を用いる。
そして、そのように、積分定数Cと組み合わせて生み出した不定積分の関数毎に:
というように、関数名F1(x)やF2(x)を付けて明確に関数を区別して計算すれば良いです。
そうすれば、関数の履歴をいちいち考える煩わしさも無くなり、明瞭に計算を進める事ができます。
《定積分の形で計算するのが良い》
以上のような不定積分の積分定数Cの扱いの煩わしさから解放されるには、定積分の積分範囲[a,x]での積分の形で不定積分を置き換えて表して、その形の式を扱い、それを計算の基本にすれば良いと思う。
リンク:
高校数学の目次
という式で定義された関数S(x)が純粋な不定積分であって、1つながりのグラフになります。
この積分の起点の値aを変えるとS(x)の値が変わるので、S(x)には、積分定数Cで表せる任意性があります。
不定積分の詳しい説明は、ここをクリックした先のページを参照してください。
【定義を拡大した不定積分】__任意の積分定数を加える__
被積分関数f(x)が:
f(x)=0
という場合を考えます。
この関数f(x)を、
f(x)が定義されている区間における、
a≦x≦b
の範囲のxまで積分します。
積分結果の関数S(x)の値が、積分の起点のaの値を変えた場合にどうなるかを調べてみます。
すると、常に、
となってしまい、この計算で得た不定積分は、aを変えても値が変わらず、積分定数Cの値が任意の値にまで変化しません。
そういう事があるので、不定積分S(x)を、微分するとf(x)になる全ての関数F(x)にまで、定義を拡大します。
すなわち、不定積分F(x)を、
と定義し、
純粋な不定積分S(x)に任意の積分定数Cを加えた関数F(x)にまで不定積分の定義を拡大します。
ただし、積分定数Cは、どの数値でも良いが、ある固定した値をCという記号であらわしているに過ぎないものです。
すなわち、積分定数Cは、関数F(x)に、普通の関数とは異なる正体不明な不定性という性質を帯びさせるというものでもありません。定数Cはありふれた1つの定数に過ぎないものです。
ただし、ある不定積分の式の積分定数Cとして、ある1つの定数を選んだ場合、その定数Cの値は、その不定積分の式を使った一連の計算の中で、一貫して、同じ値にしなければなりません。計算の途中でCの値を変えてはいけないのです。
すなわち、計算の途中のどこに出て来る不定積分同士の間でも、
を成り立たせなければなりません。
それは、(同じ履歴の)値 0 の不定積分の場合でも、
を成り立たせます。
(ただし、履歴の異なる2種類の、値 0 の不定積分がある場合は、それらの異なる2種類の関数を区別して考えなければならない。)
履歴の異なる2種類の不定積分(被積分関数f(x)は同じ)については、それらの不定積分が異なる関数なので、異なる式で記述したいです。しかし、不定積分の表し方は、同じ式の ∫f(x)dx としか表せないので、その履歴を区別する事が困難です。これは悩ましい問題です。
純粋な不定積分であれば、この様なあいまいさに由来する問題はありません。
定義を拡大した不定積分では積分定数Cの定義が拡大されていますが、
不定積分の正しい計算は、定義を拡大した不定積分であっても、純粋な不定積分:
の計算に反しない計算が正しい計算であると考えます。
不定積分の定義を拡大した副作用として生じた以下の誤りに陥らないように注意する必要があると思います。
不定積分同士の引き算:
というふうにして、F(x)-F(x)=Cとして解く解き方がしばしば使われています。
しかし、それは、誤った解き方だと考えます。
値0の不定積分は:
というふうに、積分定数Cを使って定義されます。
しかし、同じ2つの不定積分の引き算の場合には、値0の不定積分を使う必然性も無く、また、同じ不定積分で一貫して同じ値の積分定数がキャンセルされて無くなってしまうので、値が0になります。

となります。
一方で、
が成り立つため、不定積分同士の引き算の式に、どうしても0の不定積分を導入しなければならない場合は:
と計算しなければならないと考えます。
(同じ履歴の関数同士の場合の)値 0 の不定積分でも:
とします。
間違った計算:
の具体例として、
例えば、以下の例の様に、積分定数Cの値を具体化すれば、
の2つの関数を考えることができます。
不定積分の関数F(x)を1つ定義したときには、そのうちの1つのみが選択されなければなりません。
しかし、そうせずに、不定積分を、
とあらわしてあいまいにしてから、
F(x)の積分定数を一貫させずに、
という計算をしてはいけない。
という誤った不定積分の引き算の計算は、そういう誤った計算をしている。
そのような誤りを犯さずに、
F(x)-F(x)=0として解く解き方が、正しい解き方であると考えます。

となるように、不定積分は、一貫して同じ不定積分のみを使って計算するのが正しい解き方であると考えます。
(しかし、∫0dx の場合は、一貫して同じ不定積分のみを記述するというルールで縛る事ができず、頻繁に異なる履歴の不定積分が出現してしまう、悩ましい問題があります。)
誤った計算をして、同じ履歴の不定積分同士の引き算を、
F(x)-F(x)=C
としてしまい、
その式を変形して、
0=C,かつ,C≠0
とするような矛盾を持ち込むべきでは無いと考えます。
そのため、以下の様な計算は間違っていると考えます。
不定積分は、定数を無限に増殖させる正体不明な関数というものでは無いので、上の式の様に定数が生み出されるという事はありません。
また、「上の式4’の左辺の不定積分は、右辺では任意性のある積分定数Cを含む式であらわされるべきだから、この式4’の右辺に積分定数Cを加える」というのも、
本末転倒な議論です。
右辺に積分定数Cが無い式4’が得られた時点で、
どこかで計算の間違いを犯したと判断するべきです。
その計算間違いを、答えの形をつくろう事でごまかすべきでは無いと考えます。そうならないように、先行する式から、以下で説明する、(推奨される式)を書いておいて備えておくべきと考えます。
【推奨される式の記述】
複数の(定義を拡大した)不定積分の加減算を行う場合は特に慎重に行う必要があります。
という計算を行わなければならない場合も生じ得るからです。
この問題に対応するには、不定積分の加減算の計算の式の最後には必ず積分定数Cを加えるようにしなければならないとも考えます。
すなわち、以下の式の様に、式の右辺に積分定数Cを加えて書くのが望ましいと考えます。
(推奨される式) 後の式(6)
ただし、演算の筋が通らない:
という式を書いてはいけない。
また、積分の変換をした直後等の、タイミングの良い式から、推奨される式の形で積分定数Cを混ぜるべきです。
(注意)1つの式の中に不定積分が複数あれば、積分定数が不定積分の中に吸収されて調整するから積分定数を省略して良いと教わったかもしれません。例えば、部分積分法が、積分定数Cを省略した形で教えられています。
しかし、それは誤りです。
不定積分を部分積分で計算するときには、以下に示す、正確な部分積分の公式を使わなければなりません。

(注意)この式1が正しい部分積分の公式ですが、普通は部分積分の公式に付随する第1の積分定数Cは省略して書かない(この第1の積分定数Cは、残った不定積分の項を積分したときに出て来る第2の積分定数Cとは異なるものです)。しかし、問題を正しく解くためには、この公式の第1の積分定数Cを省略できない。
その式の中のある項の不定積分が他の項の不定積分と同じ式であるという紐付きの不定積分の式があります。そういう場合には、その紐付きの不定積は、積分定数を吸収して調整する事が出来ません。そういうときには、(例えば部分積分の公式で)式の中に書くべき積分定数を省略してはいけません。
【怪しい公式】
式1が成り立つと教わって来たと思います。しかし、以下に説明するように、この式1の根拠は怪しいと考えます。
k=0の場合には:
この場合に、式1と同様な式2が成り立つでしょうか。
しかし、
「式2にはならず、以下の式3が成り立つ」
と教わったと思います。
もし、式3になるならば、同様にして、以下の式4にもなるハズです。
(ただし、|k|≠1)
実際、以下の計算で式4が導き出されます。
(|k|=1の場合は、式4の積分定数Cは0になります)
そして、式4の方が式1よりも正しい式であると考えます。
なぜなら、式3も式4も、
(推奨される式) 後の式(6)
と同じ形の式だからです。
推奨される式と同じ形の式3と式4が成り立ち、
式1の根拠は無いと考えるのが正しいと思います。
そもそも、式1の形の公式は、大学で学ぶ正しい微分積分では、定積分の公式、又は、純粋な不定積分の公式として学ぶ公式であって、定義を拡大した不定積分に対して成り立つ公式では無いのです。
(正しい公式)
です。式4の、k=0の場合が式3です。
また、式3' では、値 0 の不定積分であっても、
が成り立ちます。
しかし、値 0 の積分は、
(同じ履歴の)値 0 の不定積分の場合は、
が成り立たちますが、
履歴が異なる値 0 の不定積分も同じ積分記号で表現されていて区別できない問題があります。
(履歴が異なる)値 0 の不定積分の場合は、
となってしまう問題があります。
計算の履歴が分からない、値 0 の不定積分同士の差は、上の式の様に、0とならない場合もあり得る積分定数Cであらわさざるを得ないという問題があります。
(不定積分が同じ履歴か否かは、その不定積分が導き出される演算過程を見ることで判別できます。)
同じ履歴の不定積分同士の関係であって、明らかに等号が成り立つ、|k|=1の場合の式5や、式7や、
式全体に0を掛け算して明らかに0になる式、
以外では、いずれの不定積分の演算にも積分定数Cの不定性が入り込むと考えるのが良いと考えます。
また、その様に注意深く積分定数を入れた式を使って計算しないと、明らかに成り立つ式7に対して、積分定数Cが加わった以下の式が得られてしまい、
同じ履歴の不定積分の2つの項の引き算の結果を0にすると:
0=C and C≠0,
という式になる。
という矛盾に導かれてしまいます。
高校数学の微分積分の教えでは、
不定積分の演算では、
0=C and C≠0,
が導き出されるのが当たり前である、
と教えられている様です。
そのようになるため、不定積分の項同士を引き算する正しい演算はしてはいけない演算であると教えられている様です。
それを教わった高校生は、「正しい演算規則であっても、それを使っていけない場合がある。正しい演算規則とは何?」と考え、微分積分が分からなくなるだろうと考えます。
2つの不定積分の項を引き算して 0 にしてはいけない場合は、同じ形に表現された2つの不定積分が異なる履歴を持つ場合です。
(関数の履歴を考える煩わしさからの開放)
不定積分の履歴が同じか、異なるか、履歴を気にせず計算するには、計算の中に新たな不定積分を導入する都度:
で積分定数Cを定義した関数を用いる。
そして、そのように、積分定数Cと組み合わせて生み出した不定積分の関数毎に:
というように、関数名F1(x)やF2(x)を付けて明確に関数を区別して計算すれば良いです。
そうすれば、関数の履歴をいちいち考える煩わしさも無くなり、明瞭に計算を進める事ができます。
《定積分の形で計算するのが良い》
以上のような不定積分の積分定数Cの扱いの煩わしさから解放されるには、定積分の積分範囲[a,x]での積分の形で不定積分を置き換えて表して、その形の式を扱い、それを計算の基本にすれば良いと思う。
リンク:
高校数学の目次