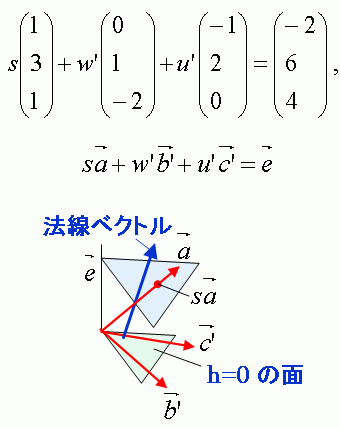
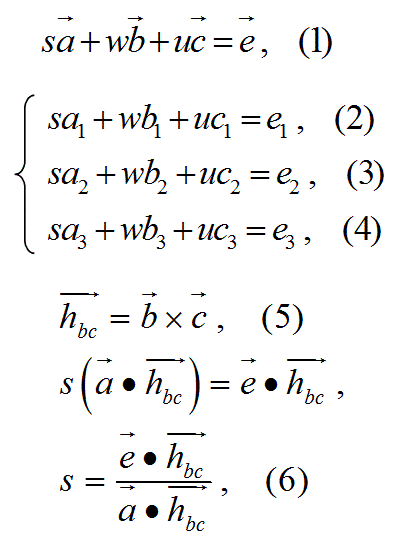【問】
実数a,bに関する条件p,qを次のように定める。
p: (a+b)2+(a-2b)2<5
q: (a+b)2<1 または (a-2b)2<4
次の①~④のうち、命題「q⇒p」に対する反例になっているのはどれか。
(反例候補)
①a=0,b=0
②a=1,b=0
③a=0,b=1
④a=1,b=1
【解答】
命題「q⇒p」に対する反例は、
q及び(pで無い)が成り立つ場合である。
(1)命題pとqをパラメータaとbであらわす式が複雑なので、命題の式の方をX、Yとおいて命題を見やすくする
(2)命題qが複雑なので、命題rとsの2つの命題に分けて、命題qを(rまたはs)に変換ずる。
r: (a+b)2<1
s: (a-2b)2<4
命題「q⇒p」に対する反例は、
(rまたはs)及び(pで無い)が成り立つ場合である。
この命題の範囲は、以下の式のように変換する。
(rまたはs)については、
(rまたは(s及び(rで無い)))
として、重なりが無い反例範囲に分ける。
そして、結局、反例範囲を、AとBとの2つに分ける。
(問題を簡単にする工夫)
このAとBとについて、別々に反例をさがす。
このAとBの反例範囲には、範囲の重なりが無いので反例探しに無駄が無い。
AとBとを別々に探すと、反例範囲の図は正確に書かないでも良く、図が簡単に手間がかからないようになる。
先ず、反例範囲Aに反例候補①②③④が入るかを調べる。
反例範囲を以下の図の斜線であらわす。
③の、a=0,b=1の場合は、
X=1なので、rを満足しない。よって反例では無い。
次に、反例範囲Bに反例候補①②③④が入るかを調べる。
③の、a=0,b=1の場合は、
Y=-2なので、sを満足しない。よって反例では無い。
④の、a=1,b=1の場合は、
X=2,Y=-1なので、sを満足する。
また、円周上の点なので、(pで無い)も満足する。
よって、④が反例である。
(解答おわり)
リンク:
高校数学の目次
実数a,bに関する条件p,qを次のように定める。
p: (a+b)2+(a-2b)2<5
q: (a+b)2<1 または (a-2b)2<4
次の①~④のうち、命題「q⇒p」に対する反例になっているのはどれか。
(反例候補)
①a=0,b=0
②a=1,b=0
③a=0,b=1
④a=1,b=1
【解答】
命題「q⇒p」に対する反例は、
q及び(pで無い)が成り立つ場合である。
(1)命題pとqをパラメータaとbであらわす式が複雑なので、命題の式の方をX、Yとおいて命題を見やすくする
(2)命題qが複雑なので、命題rとsの2つの命題に分けて、命題qを(rまたはs)に変換ずる。
r: (a+b)2<1
s: (a-2b)2<4
命題「q⇒p」に対する反例は、
(rまたはs)及び(pで無い)が成り立つ場合である。
この命題の範囲は、以下の式のように変換する。
(rまたはs)については、
(rまたは(s及び(rで無い)))
として、重なりが無い反例範囲に分ける。
そして、結局、反例範囲を、AとBとの2つに分ける。
(問題を簡単にする工夫)
このAとBとについて、別々に反例をさがす。
このAとBの反例範囲には、範囲の重なりが無いので反例探しに無駄が無い。
AとBとを別々に探すと、反例範囲の図は正確に書かないでも良く、図が簡単に手間がかからないようになる。
先ず、反例範囲Aに反例候補①②③④が入るかを調べる。
反例範囲を以下の図の斜線であらわす。
③の、a=0,b=1の場合は、
X=1なので、rを満足しない。よって反例では無い。
次に、反例範囲Bに反例候補①②③④が入るかを調べる。
③の、a=0,b=1の場合は、
Y=-2なので、sを満足しない。よって反例では無い。
④の、a=1,b=1の場合は、
X=2,Y=-1なので、sを満足する。
また、円周上の点なので、(pで無い)も満足する。
よって、④が反例である。
(解答おわり)
リンク:
高校数学の目次