

複素数の計算を推進する以下の公式を導きだしましょう。
(第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
(優先順位の2位以下のこと)
それよりは優先順位が低いことですが、以下のような、複素数平面の計算の公式の導き出し方を身に付けると、少し計算が推進されますので、以下の公式も、簡単に導き出せるようになればとても良いと思います。
以下の公式も導き出して、計算を推進させてください。
上の式の各行が、各公式をあらわしていて、
3つの公式があります。
(1)2つのベクトルの張る第1の三角形の余弦定理
(2)2つのベクトルの張る第2の三角形の余弦定理
(3)2つのベクトルの内積の、合成ベクトルの2乗の差への変換公式(余弦定理に類似した中線の式)
です。
それらの公式は、
「ベクトルの内積の和と積の公式のページ」にもあります。
また、上式の3行目の式の形を変えて得られる以下の公式は式の変形に便利:

また、上式であらわしたベクトルαとベクトルβの内積は、一方のベクトルの先端の点が他方のベクトルに垂直な方向に移動しても、両ベクトルの内積の値が変わりません。
そのため、以下の公式が成り立ちます。
また、もっと一般的な公式として、任意の実数kのパラメータを使った以下の公式も成り立ちます。
また、以下の実数化公式が成り立ちます:

また、単位ベクトルに関して以下の公式が成り立ちます:
が成り立ちます。
複素数の(1+単位ベクトルα)の偏角は、
複素数の単位ベクトルαの偏角の半分だからです。
も成り立ちます。
また、2つの単位ベクトルに関して、以下の公式が成り立ちます。
以下の式も成り立ちます。
以下の式も成り立ちます。
また、以下の公式が成り立ちます。
が成り立つ。
また、2つの単位ベクトルに関して:
が成り立つ。
また、3つ以上の単位ベクトルに関して:
が成り立つ。
同様にして、以下の公式が成り立つ。
が成り立つ。
(3つの複素数の式変換公式)
αとβの絶対値が異なっても以下の公式が成り立つ。
(3つの複素数の式変換公式(その2))
(4つの複素数の式変換公式)
以上の公式は使う場合が多いと思いますので、計算の中で必要に応じてすぐ導き出して使えたら良いなと思います。
リンク:
高校数学の目次
(第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
(優先順位の2位以下のこと)
それよりは優先順位が低いことですが、以下のような、複素数平面の計算の公式の導き出し方を身に付けると、少し計算が推進されますので、以下の公式も、簡単に導き出せるようになればとても良いと思います。
以下の公式も導き出して、計算を推進させてください。
上の式の各行が、各公式をあらわしていて、
3つの公式があります。
(1)2つのベクトルの張る第1の三角形の余弦定理
(2)2つのベクトルの張る第2の三角形の余弦定理
(3)2つのベクトルの内積の、合成ベクトルの2乗の差への変換公式(余弦定理に類似した中線の式)
です。
それらの公式は、
「ベクトルの内積の和と積の公式のページ」にもあります。
また、上式の3行目の式の形を変えて得られる以下の公式は式の変形に便利:

また、上式であらわしたベクトルαとベクトルβの内積は、一方のベクトルの先端の点が他方のベクトルに垂直な方向に移動しても、両ベクトルの内積の値が変わりません。
そのため、以下の公式が成り立ちます。
また、もっと一般的な公式として、任意の実数kのパラメータを使った以下の公式も成り立ちます。
また、以下の実数化公式が成り立ちます:

また、単位ベクトルに関して以下の公式が成り立ちます:
が成り立ちます。
複素数の(1+単位ベクトルα)の偏角は、
複素数の単位ベクトルαの偏角の半分だからです。
も成り立ちます。
また、2つの単位ベクトルに関して、以下の公式が成り立ちます。
以下の式も成り立ちます。
また、以下の公式が成り立ちます。
が成り立つ。
また、2つの単位ベクトルに関して:
が成り立つ。
また、3つ以上の単位ベクトルに関して:
が成り立つ。
同様にして、以下の公式が成り立つ。
が成り立つ。
(3つの複素数の式変換公式)
αとβの絶対値が異なっても以下の公式が成り立つ。
(3つの複素数の式変換公式(その2))
(4つの複素数の式変換公式)
以上の公式は使う場合が多いと思いますので、計算の中で必要に応じてすぐ導き出して使えたら良いなと思います。
リンク:
高校数学の目次














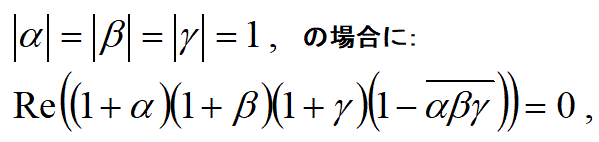


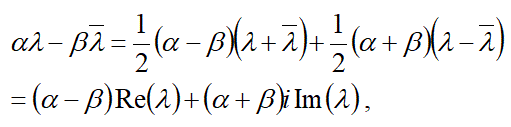


0 件のコメント:
コメントを投稿