「微分・積分」の勉強
【逆関数の微分の公式の定義】
変数ｘのある連結区間の全ての実数ｘに対して定義されている関数：
という関数f(x)があるものとする。
例えば以下の関数を考える。
また、そのｘの区間内（例えば区間(-π/2,π/2)）の全ての実数の変数ｘで f(x)が微分可能であるものとする。
また、その区間内では、以下の条件：
を満足するものとする。
例えば以下の条件を満足する。
その場合は、その変数ｘの区間では、
関数f(x)は単調増加関数か単調減少関数になる。
そのため、その変数ｘを変数ｙの関数とする逆関数：
が存在する。
例えば以下の逆関数が存在する。
逆関数g()についても、以下の条件：
を満足するものとする。
その場合には、そのｘの区間でのf(x)に対してy=f(x)で対応するyの区間における逆関数g(y)の微分を、関数f(x)の微分を用いて、以下の式：
で表す事ができる。
例えば、逆関数の微分を以下の式であらわすことができる。
（注意）df(x)/dxは、有限の値である場合のみが定義されていて、無限大にはならない。そのため、この公式において、dg(y)/dy≠0の場合に限って公式が定義されている。すなわち、この公式は、ｆ'(x)≠０とg'(y)≠０を前提にした公式である。
先ず、関数f(x)=yとその逆関数g(y)=xを考え、その後で関数の微分の関係を考える。ここで、f()に逆関数g()がある場合でも、下図のように、変数xのある値でｆ’(x)＝０となる事もあり得る。
（そのように、ｆ’(x)＝０となる変数ｘの点での関数値f(x)＝ｙの値yを変数値yの１つに持つ逆関数値g(y)=xもあり得る）
その場合は、その変数yの値に対応する関数g(y)の微分g'(y)の値が無限大に発散する。そのため、その点では、関数f(x)の微分f '(x)と関数g(y)の微分g'(y)の関係は定義できない。
（ｙ＝０で逆関数の微分の公式が定義できない逆関数g(y)の例）
（逆関数の例おわり）
すなわち、下図の関数f(x)の集合の図に示すように、全ての点で逆関数の微分の公式が成り立つ関数の集合は、逆関数を持つ関数の集合の中の一部なのである。
《恒等式の両辺を微分する演算》
上の例の逆関数の式では：
ｘ＝g(y)
が成立している場合に、その式の両辺をｘで微分した式：
１＝ｄg(y)/ｄx
を求める計算をすることがある。
（ただし、y=f(x)の関数f(x)の逆関数x=g(y)が存在することが大前提である）
▷（演算結果の有効性の条件１：微分可能であること）
両辺をｘで微分する計算をする場合に、その結果得られた等式は、全ての項が微分可能な場合のみに、得られた等式が有効になる。
上記の例の等式の両辺を微分する場合は、
関数f(x)に逆関数g(y)があっても、逆関数g(y)が微分できない点（dy/dx=f '(x)=0となる点で、x=g(y)はｙで微分できない）があるので、その点では右辺の項が微分可能ではない。その点では、得られた式は無効である。
▷（演算結果の有効性の条件２：元の等式の変数ｙに、ｘの関数f(x)を代入した等式 x=g(f(x))が恒等式になること。（「円の接線の公式を微分で導く」のページも参照）
（変数ｘの恒等式ではない例）
例えば、
x=5,
という式の両辺をｘで微分した式：
1=0,
は間違った式である。
この式は、元の式が変数ｘの恒等式ではなかったからである。そういう、変数ｘの恒等式ではない元の式の両辺を微分した式は、以上の式のように間違った式になる、無効な式である。
式の両辺を微分する計算には要注意。
（両辺の微分演算の前提条件おわり）
条件２（恒等式）については、
の式の関数g(y)は、y=f(x)という関数の逆関数であって、変数 y にｘの関数f(x)を代入すると、式１の右辺が恒等的にｘになる場合に式(1)が変数ｘの恒等式とみなせる。
すなわち、式(1)のyにf(x)を代入した以下の式(2)の右辺も左辺と同じｘになる。
例えば、先の例の関数f(x)及び逆関数g(y)では、前提条件をｘ≧０,ｙ≧０，とした場合は、式(2)の右辺が以下のように変換される。
上記のように、ｘ=ｘという、変数ｘの恒等式になる。
（これが成り立つ前提条件として、f(x)に対する逆関数g(y)が存在することが必須な条件である）
式(2)が変数ｘの恒等式ならば、その恒等式をｘで微分した結果も1=1になり、その式は正しい式になる。
この式(2)の両辺をｘで微分した結果、右辺の微分を合成関数の微分の公式であらわすと、以下の式(3)を得る。
演算結果の有効性の条件１（微分可能）については、
g(y)がyで微分可能であり、f(x)がｘで微分可能である必要がある。
g(y)がyで微分可能である条件は、関数g()の逆関数f()に関して、
f(x)の微分が０で無い
ｆ'(x)≠0
となることが前提条件に必要である。
f(x)がｘで微分可能である条件は、関数f()の逆関数g()に関して、
g(y)の微分が０で無い
g'(y)≠0
となることが前提条件に必要である。
その２つの前提条件を満足する式が有効な式である。
例えば、
式(3)で、x=0において、f '(x)=0であったら、その場合に、逆関数g(y)がx=0の点に対応するｙの値において微分可能ではないので、x=0での式(3)は成立できず、無効である。
f()もg()も微分可能である有効な式に限るならば、x=0において式(3)から、
1=0,
という式が出て来るということは起こらない。
もっと具体的に、逆関数の微分の公式が成り立つ前提条件を、論理的帰結を組み込んで整理して記載すると、
「ｘの所定区間で、f(x)が微分可能であって、かつ、逆関数g(y)=xが存在してg(y)が変数ｙで微分可能である。そのために、f '(x)≠0 であること」
が前提条件に必要である。その結果、
「f(x)が狭義の単調増加関数であるか単調減少関数である。」
その前提条件によって、
「f(x)=ｙの値域もｙの値が連結された区間になり、その区間の値域を定義域とする逆関数x=g(y)が狭義の単調関数であり、g(y)が微分可能でありg'(y)≠０である」
ということが前提条件に必要である。
この前提条件（逆関数の微分の公式が成り立つ関数の限定範囲）を明示しないで記述された逆関数の微分の公式の説明にはごまかしがある。
その前提条件の下で、式(3)の両辺が微分されて式(3)が得られる。そして、その式(3)を変形する事で、先の逆関数の微分の公式：
と、以下の形の逆関数の微分の公式とが成り立つ。
（逆関数の微分の公式の定義おわり）
このように逆関数の微分の公式が成り立つための関数の条件は、この関数を使って関数を変換するならば、微分不可能な関数が微分可能な関数に変換することがない、節度のある関数の条件でもある。
なお、逆関数の微分の公式は以下の式ではないので、要注意です。
（補足）
以下の関数f(x)で：
(df(x)/dx)=0となっているグラフの部分（ｙ＝０の部分）については、以下の逆関数g(y)のグラフの様に:
ｙ＝０となっているグラフの部分では、逆関数g(y)が存在しない。 そして、g(y)のｙ＝０での右側極限と左側極限が一致しない。そのため、Δｙ→０の場合にΔｘ→０とはならない。
一方、y=f(x)のグラフにおいて、(df(x)/dx)=０となるのは点だけであって幅のある区間ではそうならない、単調増加（又は単調減少）な関数f(x)には逆関数g(y)が存在する。
(df(x)/dx)=０となる点で関数を切って分割してしまって、そのように分割した個々の関数毎に逆関数の微分の公式を考えれば良い。
【逆関数の微分の公式の証明】
以下で、逆関数の微分の公式を、もう少し厳密に証明する。
（証明開始）
（１）先ず、逆関数の微分の公式の前提条件を明確にしておく。
（２）次に、逆関数の微分の公式が成り立ち得る、微分可能な逆関数を持つ、微分可能な関数f(x)の条件を明確にしておく。
で表せる、１つながりに連続な関数f(x)が微分可能（（Δf(x)／Δｘ）の極限が有限の値になる）である場合であって、
その関数の微分が、
を満足する変数ｘの区間では、関数f(x)が単調増加か単調減少である。
その区間では、その変数ｘを変数ｙの関数と考えた逆関数
が存在する。
（３）そして、この種の逆関数ｘ＝g(y)をｙで微分する式を求める。
ｙ=ｆ(ｘ)がｘで微分可能であるので、
Δｙが以下の式であらわされる。
ここで、 Δｙ／Δx=Δf(x)／Δx≠０
なので、
Δｙ→０の場合に、Δｘ＝Δｙ／(Δf(x)／Δx)→０になる。
（４）以上の前提条件が成り立つ場合に、以下の式が計算できる。Δｙ≡Δf(x)という関数を対象にしていて、また、逆関数のΔｘ≡Δg(y)という関数を対象にしていることをしっかり認識して計算する。（また、Δg(y)≡Δｘ≠０であることに注意する）
（証明おわり）
こう考えれば逆関数の微分の公式が自然に証明できます。
上の公式は、下のグラフのように、逆関数は、元の関数に対して、直線ｙ＝ｘに関して対称なので、その傾きが元の関数の傾きに対して、対称な傾きである、逆数の値の傾きになる、
ということを意味している。
ここで、逆関数の微分の公式の縛り（成立条件）である
「ｘのｙによる微分が存在する（確定した有限値になる）」、
という前提条件は、
「式を０で割り算する計算をしてはいけない」
という計算の縛りと同じ様な意味を持っています。
すなわち、「微分可能」という前提条件は、
「０で割り算しない場合に限る」という前提条件 、
言いかえると、
「計算の違反が無い計算に限る」という前提条件、
を加えて微分の式を書くことです。
そういう「万能の条件」を正しく組み込んで計算するならば、どの様な計算もできてしまいます。
その通りに、どの様な計算もできるのが、逆関数の微分の公式やその他の公式が成り立つ根拠だと考えます。
リンク：
高校数学の目次
【逆関数の微分の公式の定義】
変数ｘのある連結区間の全ての実数ｘに対して定義されている関数：
という関数f(x)があるものとする。
例えば以下の関数を考える。
また、そのｘの区間内（例えば区間(-π/2,π/2)）の全ての実数の変数ｘで f(x)が微分可能であるものとする。
また、その区間内では、以下の条件：
を満足するものとする。
例えば以下の条件を満足する。
その場合は、その変数ｘの区間では、
関数f(x)は単調増加関数か単調減少関数になる。
そのため、その変数ｘを変数ｙの関数とする逆関数：
が存在する。
例えば以下の逆関数が存在する。
逆関数g()についても、以下の条件：
を満足するものとする。
その場合には、そのｘの区間でのf(x)に対してy=f(x)で対応するyの区間における逆関数g(y)の微分を、関数f(x)の微分を用いて、以下の式：
で表す事ができる。
例えば、逆関数の微分を以下の式であらわすことができる。
（注意）df(x)/dxは、有限の値である場合のみが定義されていて、無限大にはならない。そのため、この公式において、dg(y)/dy≠0の場合に限って公式が定義されている。すなわち、この公式は、ｆ'(x)≠０とg'(y)≠０を前提にした公式である。
先ず、関数f(x)=yとその逆関数g(y)=xを考え、その後で関数の微分の関係を考える。ここで、f()に逆関数g()がある場合でも、下図のように、変数xのある値でｆ’(x)＝０となる事もあり得る。
（そのように、ｆ’(x)＝０となる変数ｘの点での関数値f(x)＝ｙの値yを変数値yの１つに持つ逆関数値g(y)=xもあり得る）
その場合は、その変数yの値に対応する関数g(y)の微分g'(y)の値が無限大に発散する。そのため、その点では、関数f(x)の微分f '(x)と関数g(y)の微分g'(y)の関係は定義できない。
（ｙ＝０で逆関数の微分の公式が定義できない逆関数g(y)の例）
（逆関数の例おわり）
すなわち、下図の関数f(x)の集合の図に示すように、全ての点で逆関数の微分の公式が成り立つ関数の集合は、逆関数を持つ関数の集合の中の一部なのである。
《恒等式の両辺を微分する演算》
上の例の逆関数の式では：
ｘ＝g(y)
が成立している場合に、その式の両辺をｘで微分した式：
１＝ｄg(y)/ｄx
を求める計算をすることがある。
（ただし、y=f(x)の関数f(x)の逆関数x=g(y)が存在することが大前提である）
▷（演算結果の有効性の条件１：微分可能であること）
両辺をｘで微分する計算をする場合に、その結果得られた等式は、全ての項が微分可能な場合のみに、得られた等式が有効になる。
上記の例の等式の両辺を微分する場合は、
関数f(x)に逆関数g(y)があっても、逆関数g(y)が微分できない点（dy/dx=f '(x)=0となる点で、x=g(y)はｙで微分できない）があるので、その点では右辺の項が微分可能ではない。その点では、得られた式は無効である。
▷（演算結果の有効性の条件２：元の等式の変数ｙに、ｘの関数f(x)を代入した等式 x=g(f(x))が恒等式になること。（「円の接線の公式を微分で導く」のページも参照）
（変数ｘの恒等式ではない例）
例えば、
x=5,
という式の両辺をｘで微分した式：
1=0,
は間違った式である。
この式は、元の式が変数ｘの恒等式ではなかったからである。そういう、変数ｘの恒等式ではない元の式の両辺を微分した式は、以上の式のように間違った式になる、無効な式である。
式の両辺を微分する計算には要注意。
（両辺の微分演算の前提条件おわり）
条件２（恒等式）については、
の式の関数g(y)は、y=f(x)という関数の逆関数であって、変数 y にｘの関数f(x)を代入すると、式１の右辺が恒等的にｘになる場合に式(1)が変数ｘの恒等式とみなせる。
すなわち、式(1)のyにf(x)を代入した以下の式(2)の右辺も左辺と同じｘになる。
例えば、先の例の関数f(x)及び逆関数g(y)では、前提条件をｘ≧０,ｙ≧０，とした場合は、式(2)の右辺が以下のように変換される。
上記のように、ｘ=ｘという、変数ｘの恒等式になる。
（これが成り立つ前提条件として、f(x)に対する逆関数g(y)が存在することが必須な条件である）
式(2)が変数ｘの恒等式ならば、その恒等式をｘで微分した結果も1=1になり、その式は正しい式になる。
この式(2)の両辺をｘで微分した結果、右辺の微分を合成関数の微分の公式であらわすと、以下の式(3)を得る。
演算結果の有効性の条件１（微分可能）については、
g(y)がyで微分可能であり、f(x)がｘで微分可能である必要がある。
g(y)がyで微分可能である条件は、関数g()の逆関数f()に関して、
f(x)の微分が０で無い
ｆ'(x)≠0
となることが前提条件に必要である。
f(x)がｘで微分可能である条件は、関数f()の逆関数g()に関して、
g(y)の微分が０で無い
g'(y)≠0
となることが前提条件に必要である。
その２つの前提条件を満足する式が有効な式である。
例えば、
式(3)で、x=0において、f '(x)=0であったら、その場合に、逆関数g(y)がx=0の点に対応するｙの値において微分可能ではないので、x=0での式(3)は成立できず、無効である。
f()もg()も微分可能である有効な式に限るならば、x=0において式(3)から、
1=0,
という式が出て来るということは起こらない。
もっと具体的に、逆関数の微分の公式が成り立つ前提条件を、論理的帰結を組み込んで整理して記載すると、
「ｘの所定区間で、f(x)が微分可能であって、かつ、逆関数g(y)=xが存在してg(y)が変数ｙで微分可能である。そのために、f '(x)≠0 であること」
が前提条件に必要である。その結果、
「f(x)が狭義の単調増加関数であるか単調減少関数である。」
その前提条件によって、
「f(x)=ｙの値域もｙの値が連結された区間になり、その区間の値域を定義域とする逆関数x=g(y)が狭義の単調関数であり、g(y)が微分可能でありg'(y)≠０である」
ということが前提条件に必要である。
この前提条件（逆関数の微分の公式が成り立つ関数の限定範囲）を明示しないで記述された逆関数の微分の公式の説明にはごまかしがある。
その前提条件の下で、式(3)の両辺が微分されて式(3)が得られる。そして、その式(3)を変形する事で、先の逆関数の微分の公式：
と、以下の形の逆関数の微分の公式とが成り立つ。
（逆関数の微分の公式の定義おわり）
このように逆関数の微分の公式が成り立つための関数の条件は、この関数を使って関数を変換するならば、微分不可能な関数が微分可能な関数に変換することがない、節度のある関数の条件でもある。
なお、逆関数の微分の公式は以下の式ではないので、要注意です。
（補足）
以下の関数f(x)で：
一方、y=f(x)のグラフにおいて、(df(x)/dx)=０となるのは点だけであって幅のある区間ではそうならない、単調増加（又は単調減少）な関数f(x)には逆関数g(y)が存在する。
(df(x)/dx)=０となる点で関数を切って分割してしまって、そのように分割した個々の関数毎に逆関数の微分の公式を考えれば良い。
【逆関数の微分の公式の証明】
以下で、逆関数の微分の公式を、もう少し厳密に証明する。
（証明開始）
（１）先ず、逆関数の微分の公式の前提条件を明確にしておく。
（２）次に、逆関数の微分の公式が成り立ち得る、微分可能な逆関数を持つ、微分可能な関数f(x)の条件を明確にしておく。
その関数の微分が、
その区間では、その変数ｘを変数ｙの関数と考えた逆関数
（３）そして、この種の逆関数ｘ＝g(y)をｙで微分する式を求める。
ｙ=ｆ(ｘ)がｘで微分可能であるので、
Δｙが以下の式であらわされる。
なので、
Δｙ→０の場合に、Δｘ＝Δｙ／(Δf(x)／Δx)→０になる。
（４）以上の前提条件が成り立つ場合に、以下の式が計算できる。Δｙ≡Δf(x)という関数を対象にしていて、また、逆関数のΔｘ≡Δg(y)という関数を対象にしていることをしっかり認識して計算する。（また、Δg(y)≡Δｘ≠０であることに注意する）
（証明おわり）
こう考えれば逆関数の微分の公式が自然に証明できます。
上の公式は、下のグラフのように、逆関数は、元の関数に対して、直線ｙ＝ｘに関して対称なので、その傾きが元の関数の傾きに対して、対称な傾きである、逆数の値の傾きになる、
ということを意味している。
ここで、逆関数の微分の公式の縛り（成立条件）である
「ｘのｙによる微分が存在する（確定した有限値になる）」、
という前提条件は、
「式を０で割り算する計算をしてはいけない」
という計算の縛りと同じ様な意味を持っています。
すなわち、「微分可能」という前提条件は、
「０で割り算しない場合に限る」という前提条件 、
言いかえると、
「計算の違反が無い計算に限る」という前提条件、
を加えて微分の式を書くことです。
そういう「万能の条件」を正しく組み込んで計算するならば、どの様な計算もできてしまいます。
その通りに、どの様な計算もできるのが、逆関数の微分の公式やその他の公式が成り立つ根拠だと考えます。
リンク：
高校数学の目次
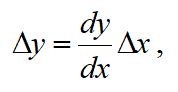
0 件のコメント:
コメントを投稿