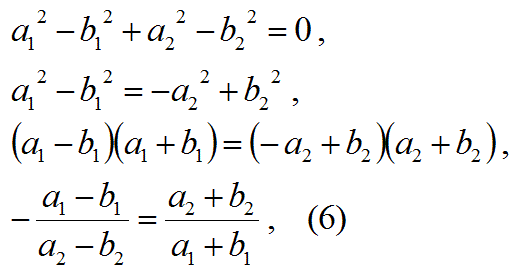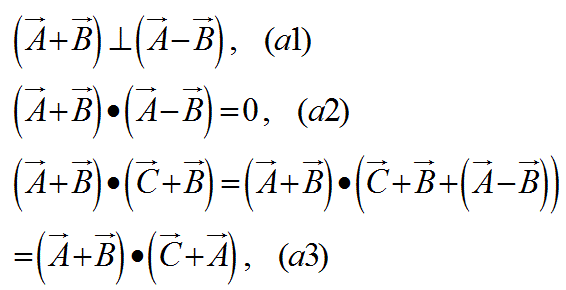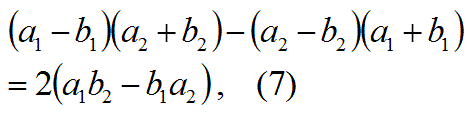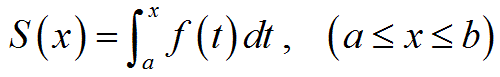ページ
▼
以下の「ひし形の対角線の直交の公式」は、このページの読者の心の隅っこのどこかに残れば良いと思います。ガチガチに覚えないようにして、数学を楽しんで欲しいと思います。
読者が、この公式が必要になった時に、「たしか、そのような式がありそうな気がする」と思いだして、読者が自力でこの公式を導き出して使えたら良いと考えます。
（公式は全て、必要な時に自力で導き出して、それが使えれば良いと思います。）
【ひし形の対角線の直交の公式】
下図のひし形ＯＡＫＢの２つの対角線ＯＫとＡＢが互いに直交することが、
以下の図の線分ＯＫの傾きが、線分ＡＢに平行な線分ＯＨの傾きの逆数×（－１）である、ことにより証明できます。
【公式の証明】
（ＯＡ）２－（ＯＢ）２：
ー１／（ＯＨの傾き）＝（ＯＫの傾き）
∴ ＯＫとＯＨは直交する。
∴ ＯＫとＡＢは直交する。
「この式６の左右の項が互いに置き換えられる」
ということが、
ひし形の対角線の直交の公式です。
（ひし型の対角線の直交の公式おわり）
（補足）この公式を逆にして認識した方が良いかもしれない。
ひし形の対角線が互いに直交することは幾何学的に証明できます。
そして、この公式の逆の証明により、線分ＯＫと線分ＡＢが互いに直交する場合は：
ー１／（ＡＢの傾き）＝（ＯＫの傾き）
となる事が証明できる。
なお、
ー１／（ＡＢの傾き）＝（ＯＫの傾き）
となる事も、
以上の計算をしないでも、幾何学的に証明できます。
【ひし形の対角線の直交の公式の応用】
ひし形の対角線の直交の公式は、以下のように、ベクトルの内積の式を変換する計算に使います。
上図のベクトルに関してひし形の対角線の直交の公式は、以下の式ａ１又はａ２であらわせます。
式ａ３のように、ベクトルの内積の式が、式ａ２を使って変換できます。
また、この式ａ３を使うと、以下の式ａ４であらわす、
任意の定数ｓで成り立つベクトルの内積の変換公式が作れます。
【２重平行四辺形の面積の公式】
ここで、もう１つの式７で与えられる、２重平行四辺形の面積の公式も覚えて使いましょう。
（これは、ＯＡの長さとＯＢの長さが異なっても成り立つ恒等式です）
この式７の公式は、右辺から左辺を導く公式として覚えましょう。
この式７の公式は、以下の図の２重の平行四辺形の面積の大きさの関係をあらわす公式です。
（この計算は、ベクトルの外積の計算であり、並行四辺形の面積を求める計算であるという意味を持ちます。）
（２重平行四辺形の面積の公式おわり）
この２重平行四辺形の面積の公式は、ベクトルAとBを反時計回りに９０度回転したベクトルAvとBvを使って、以下の式であらわせます。
リンク：
高校数学の目次
以下で、交差する曲線（直線も曲線の一種）の全ての交点を通る全ての直線を求める方法を調べる。
【課題】２つの曲線：
（直線１） ｙ＝０ （式１）
（放物線２） ｙ＝ｘ２ （式２）
がある。この２つの曲線の交点を全て（この場合は座標原点のみ）を通る全ての直線の式を求める方法を調べる。
この課題の曲線１（式１）と曲線２（式２）の連立方程式の解が交点（この場合は座標原点）の座標になる。
この式１と式２をどの様に使えば、その交点を全て通る全ての直線の式を求めることができるかを調べる。
（調査研究の開始）
この課題は、以下の形の式を作る問題です。
（直線３） ａｘ＋ｂｙ＝ｃ （式４）
（第１の計算方針）
新しい直線の式を求めるには： 式１を、式２に代入すると、以下の式３が得られる。
０＝ ｘ２
∴ ｘ＝０ （式３）
この式３は、新しい直線をあらわす式でもある。
式１と式３を連立すると、
任意のａとｂに関して：
ａｘ＋ｂｙ＝０ （式４）
が得られる。
この式４は、任意のａとｂに関する直線をあらわす式でもある。この式４は、式１の曲線と式２の曲線の全ての交点（原点のみ）を通る。
こうして、式１を式２に代入する計算をすれば、式１の曲線と式２の曲線の全ての交点を通る全ての直線の式を求めることができることが分かった。
（第２の計算方針）
式１と式２を重みを付けて足し合わせる計算をしてみる。
式２を変形する。
ｙ－ ｘ２ ＝０ （式２’）
（式２’）ー（式１）：
０－ｘ２ ＝０
ｘ＝０ （式３）
これによっても式３が得られる。
式１と式３を連立すると、
任意のａとｂに関して：
ａｘ＋ｂｙ＝０ （式４）
が得られる。
（補足）
この事例の場合は、第２の計算方針によっても、全ての交点を通る全ての直線を求めることができた。
しかし、後で説明する他の事例「円と円の交点」の場合では、第２の計算方針によっては、全ての交点を通る全ての直線を求めることはできない。
全ての交点を計算するには、先の図のような図を描いて答えを予測できるように計算の見通しを良くした上で、その答えが得られるように計算式を導く事が良いことが分かった。
（計算の見通しを良くするにはベクトルで考える）
式と図形の計算式の見通しを良くするには、ベクトルの概念を使って、式をまとめて（整理して）考えることが効果的です。そのため、式と図形の計算の学習と並行して、ベクトルの概念も学んでいってください。
リンク：
高校数学の目次
以下で、２円の交点を通る直線の全てを求めることができるか調べる。
【課題】２つの円、
（円１） （ｘ－１）２＋ｙ２＝１ （式１）
（円２） （ｘ＋１）２＋ｙ２＝１ （式２）
がある。この２つの円の交点を全て（この場合は座標原点のみ）を通る全ての直線の式を求める方法を調べる。
この課題の円の（式１）と（式２）の連立方程式の解が交点（この場合は座標原点）の座標になる。
この式１と式２をどの様に使えば、その交点を全て通る全ての直線の式を求めることができるかを調べる。
（調査研究の開始）
この課題は、以下の形の式を作る問題です。
（直線３） ａｘ＋ｂｙ＝ｃ （式３）
（第１の計算方針）
ｍ（式１）＋ｎ（式２）を計算することで、直線３の式を求める。
計算の見通しを良くするために、式にｍを掛け算してｍ倍になる項を全て左辺に集めた式に整えて計算する。
（円１） （ｘ－１）２＋ｙ２－１＝０ （式１’）
ｘ２－２ｘ＋１＋ｙ２－１＝０，
ｘ２＋ｙ２－２ｘ＝０ （式４）
（円２） （ｘ＋１）２＋ｙ２－１＝０ （式２’）
ｘ２＋２ｘ＋１＋ｙ２－１＝０，
ｘ２＋ｙ２＋２ｘ＝０ （式５）
（直線３の式の計算）
先ず、ｍ（式４）＋ｎ（式５）を計算することで、直線３の式を求める。
ｍ（ｘ２＋ｙ２－２ｘ）＋ｎ（ｘ２＋ｙ２＋２ｘ）＝０ （式６）
この式６を、式３と等しくなるように、ｍとｎの値を決める。
式６と式３を比較し易いように、式６を変形する。
（ｍ＋ｎ）ｘ２＋（ｍ＋ｎ）ｙ２
＋（－２ｍ＋２ｎ）ｘ
＝０， （式７）
直線の式３には、ｘ２の項やｙ２の項が無いので、上の式７もそれらの項の係数が０でなければならない。
（詳しくは、以下のように考える）
式７が式３と等しいためには、両式の各係数が等しくなければならない。
＜式７＞ ＜式３＞
ｘ２の係数： （ｍ＋ｎ） ＝０， （式８）
ｙ２の係数： （ｍ＋ｎ） ＝０， （式８と同じ）
ｘの係数： （－２ｍ＋２ｎ）＝ａ，
ｙの係数： ０ ＝ｂ，
定数項の係数： ０ ＝－ｃ，
式８以外の式は未知数ａ，ｂ，ｃを定める式であって、ｍとｎを限定する式ではないので、ｍとｎを限定するのは式８のみ。
よって、
ｍ＋ｎ＝０ （式８）
この式８の条件を満たすｍとｎのどの組合せでも良い。
とりあえず、ｍ＝１、ｎ＝－１に決める。
その場合は、式７は、以下の式になる。
（－２－２）ｘ＝０，
－４ｘ＝０，
（－４）で式全体を割り算する。
ｘ＝０ （式９）
この式９が求める式３の形（を変形した形）の具体的式である。
（注意）この式９は、式４と式５を加えて得た式であるので、式１と式２の円の交点（座標原点）を通る。
しかし、図から明らかなように、円１と円２の全ての交点（座標原点のみ）を通る直線は、この式９だけでは無い。
（結論）
式６の計算だけでは、円１と円２の全ての交点を通る全ての直線の式が得られないことがあることが分かった。
（疑問）
式６の計算によって、式４と式５を加え合わせるｍとｎの値をどの様に変えても、この式９の直線以外は得られないのだろうか、どこに見落としがあるのだろうか。
この疑問への答えを考えた結果、以下の答えが得られた。
（疑問の解決）
式９を、式４又は式５に代入すると、以下の式１０が得られる。
ｙ２＝０ （式１０）
∴ ｙ＝０ （式１１）
式９と式１１を連立すると、
任意のａとｂに関して：
ａｘ＋ｂｙ＝０ （式１２）
すなわち、任意のａとｂに関する直線が、
円１と円２の全ての交点（原点のみ）を通る。
こうして、式９を元の円の式に代入する計算をすれば、円１と円２の全ての交点を通る全ての直線の式を求めることができることが分かった。
この様に、式９を元の円の式に代入するという発想は、式９だけでは円の交点を通る全ての直線が求められていないという事が分かっているからこそ、発想できた。そのように解の全てが予測できなければ、この解には至らなかった。
（結論）
以上の考察の結果、計算する際には、その計算で得られた解が全ての解であるかが分かるように、計算の見通しを良くする事がとても大切であることが分かった。
（計算の見通しを良くするにはベクトルで考える）
式と図形の計算式の見通しを良くするには、ベクトルの概念を使って、式をまとめて（整理して）考えることが効果的です。そのため、式と図形の計算の学習と並行して、ベクトルの概念も学んでいってください。
リンク：
高校数学の目次
（ページ内リンク先）
▽基本定理の概要
▽微分積分学の基本定理の定義
▽基本定理の定義のポイント
▽基本定理の対偶
▽微分積分学の基本定理の正しい定義
▽補助定理
▽基本定理の確認
▽基本定理の前半の証明
▽基本定理の中段の証明
▽基本定理の後半の証明
▽微分と積分の関係
▽微分積分学の基本定理の拡張
《基本定理の概要》
【被積分関数の単位】
被積分関数は、均質な基本的な要素の単位で考える。
具体的には、被積分関数を、全て、１つながりに連続する関数を単位にして考える。１つながりに連続する関数は正しく定義された連続関数です。その、１つながりに連続する関数を扱うのであれば、積分の計算で誤りに陥る事を防ぐことができます。
（微分型の）《微分積分学の基本定理》
微分型で表現した微分積分学の基本定理は：
連結区間内で１つながりに連続な関数f(x)がある場合：
が成り立つというものです。
高校の微分積分の教科書では、この定理が当然に成り立つものとして、証明しないで使っています。
（高校の微分積分の参考書に以下の証明があります）
「駿台受験シリーズ 分野別 受験数学の理論7 微分法・積分法の基礎」
https://math.co.jp/contpgm2/w_main.php?oya_id=2&back_id=14#14
（９６ページ途中から）
《補足》（この証明での重要ポイント）
以上の証明の中で、関数f(x)がｘ軸上のｘの点において連続関数であるという前提条件を使っている。つまり、関数f(x)が連続関数なので、hを十分小さくすれば、f(x+h)がf(x)に近づく、という前提条件を使った。
この証明の発想の根底に、関数（グラフ）が連続であるという概念が、証明の重要なポイントになっているということに気づくことが大事だ。そこから、連続関数の性質を深く研究する、という数学の研究の焦点が絞られ、その研究の成果が、数学における極限の概念の確立などだろう。そういう、数学の根底の思想が、大学の微分積分学によって学ぶことができる。
数学の微分積分の参考書は、大学で真実を追求する参考書以外にも、以上のように、高校数学での参考書にも、数学の発想の礎を作るために良い参考書があった。
一方、高校の微分積分の教科書は偽物で、数学の発想の礎作りに役立たないと考える。
（補足おわり）
この式が成り立たない場合などあり得ないのではないか？と考える人もいるかもしれません。
この式が成り立たない場合というのは、f(x)が積分出来ない場合です。そもそも積分できなければ、微分する以前に、この式が成り立たないことになります。
また、f(x)が積分して関数F(x)が得られても、関数F(x)が折れ曲がった関数になれば、その折れ曲がり点でF(x)は微分できません。F(x)が微分できなければ、この式が成り立たないことになります。
「関数 f(x) が連結区間内で１つながりに連続している関数f(x)が積分可能である。その積分結果の関数F(x)が、その連結区間で微分可能である。そうして微分した結果は元の関数f(x)に戻る。」というのが（微分型の）微分積分学の基本定理です。
そこには、「関数 f(x) が、ある連結区間内で１つながりに連続している」という条件が付いているのです。
ーー【区間の定義】ーー
「区間」という数学用語は、変数ｘの数直線上の１つの範囲内の、実数のすき間がない１かたまりの数の集合をあらわす数学用語である。
《神奈川大学》【定義 14.2.4.】
a, b を実数とする. a 以上かつ b 以下の実数をすべて集めた集合を [a, b] と書き, これを閉区
間と呼ぶ.
a より大きくかつ b 未満の実数をすべて集めた集合を (a, b) と書き, これを開区間と呼ぶ.
----定義おわり----
ａ≦ｘ≦ｂを満足するｘの区間という表現は、ａ≦ｘ≦ｂの範囲内の全ての実数ｘという意味です。
－∞＜ｘ＜∞という区間もあります。
区間はｘの値の範囲を限定するためのａ≦ｘ≦ｂという式とは意味が異なることに注意する必要があります。
区間ａ≦ｘ≦ｂが命題の中に記載されている場合は、その範囲内の全ての実数ｘについて命題を検討する必要があります。被積分関数ｆ(x)が定義されていない変数ｘの点があっても、その点も、その命題が検討されるべき点の１つです。
「区間」という用語は、特に重要な関数である連続関数の連続性を定義するために必要な、連続関数f(x)の変数xの集合体がいつも持っていなければならない連続性という重要な性質が「区間」という概念を用いてあらわされています。
すなわち、変数ｘの「区間」の性質で大切なのは、
「区間」のなかに変数ｘの値が隙間なく存在すること。
つまり所定範囲内での隙間が無い全ての実数の集合という概念が「区間」という用語で定義されています。
例えば：
f(x)=1/xの定義域を(0,∞) (={x|xは0より大きい実数})
とすれば、f(x)は区間で定義された関数です。
g(x)=1/xの定義域を(-∞,0)∪(0,∞)(={x|xは0でない実数})
とすれば、g(x)は区間で定義された関数ではない。
（f(x)とg(x)は定義域が異なっているため、f(x)とg(x)は同じ関数ではない）
（積分型の）《微分積分学の基本定理》
先ず、以下の注意をしておきます。
【注意：間違った計算の例】
以下の図の関数F(x)を考える。
F(x)=C2, (x＜0)
F(x)=C1, (x＞0)
例えば、C1=1, C2=2, とする。
この関数F(x)を微分して積分してみます。
先ず、微分します。
F'(x)= f(x)=0, (x≠0)
次に、このf(x)を積分します。
ここで、関数f(x)が、変数ｘが定義される範囲が、連結区間内の全ての実数であること。その連結区間内の全ての実数の変数ｘで関数f(x)が定義されていなければ、その関数は（変数ｘの定義域とセットになっているのが関数です）積分してはいけません。
f(x)=0, (x＞0) は積分できます。
f(x)=0, (x＜0) も積分できます。
しかし、
f(x)=0, (x≠0) は、x≠0 の範囲でx=0の点ではf(x)が定義されていないので、その点をまたいで積分してはいけません。
もし、それを無視して無理に積分すると、
∫F'(x)dx=∫0dx=C, x≠0,
という積分になりますが、
その結果の積分定数Cをどのような値に調整しても、それは、元の関数F(x)には決してなりません。
（「元の関数F(x), (x≠0) は、変数ｘで関数F(x)が定義されるxの範囲が、x=0が除外されていることで、そのxの範囲（定義域）が、連結区間内の全ての実数では無い関数でした。）
以下で、（積分型の）微分積分学の基本定理を説明します。
（１）関数ｆ（ｘ）を、それが連続する連結区間ａ≦ｘ≦ｂ
内で定積分（定積分はリーマン積分によって定義されます）することで関数Ｓ（ｘ)を求めます。
その関数をｘの関数（不定積分）として求めます。
その不定積分は、定積分の計算を実行する苦労をして得た結果を元にして求めます。
（２）一方で、１つながりに連続で、かつ、微分可能な関数F(x)があって、そのF(x)を微分して求めた導関数がf(x)と一致するならば、その関数F(x)がS(x)と一致する。すなわち、S(x)はf(x)の原始関数の１つである。そして、そのF(x)について、
が成立する。というのが微分積分学の基本定理です。
すなわち、そのＦ(x)が、苦労して求めるべき不定積分Ｓ（ｘ）と一致することが分かりました。
そのF(x)を原始関数と名付け、
その原始関数F(x)を使うことにより計算がとても楽になったので 感動した！
という内容が、（積分型の）微分積分学の基本定理です。
-----【原始関数の正しい定義】---------------
（原始関数の正しい定義は、１つながりに連続で、かつ、微分可能な関数Ｆ(x)をｆ（ｘ）の原始関数と定義します）
すなわち、関数F(x)が、連結区間ａ＜ｘ＜ｂのどの点でも連続、かつ、微分可能な関数であれば、F(x)を微分して導関数ｆ（ｘ）が求められる。この場合に、F(x)を関数ｆ（ｘ）の原始関数と言う。
（藤原松三郎の「微分積分学 第１巻」）
すなわち、原始関数は連結区間における連続関数であり１つながりのグラフであると定義されています。
-------原始関数の定義おわり-----------------
（微分可能の定義との関係）あと、微分積分学の基本定理の根底を支えているのが微分可能の定義です。高校数学では、微分可能の定義として、右微分係数と左微分係数が一致する場合にのみ微分可能とする定義しか与えられていません。
それにより、変数ｘの閉区間(a≦x≦b)で定義された関数f(x)であっても、微分可能な変数ｘの値の範囲は開区間(a<x<b)になってしまいます。そのため、高校数学の範囲内の知識では、開区間(a<x<b)で定義された関数
f(x)にしか、微分積分学の基本定理が成り立ちません。
一方、大学数学では、変数ｘが閉区間（a≦x≦b）で定義された関数f(x)の区間の端点x=a,bでも、片側微分係数があるだけで微分可能とする微分可能の定義も与えられています。そのため、大学数学では、閉区間で定義された関数f(x)にも微分積分学の基本定理が成り立つと教えられています。
上図の関数f(x)と、下図の関数F(x)の間では、定義域がｘ＞０での被積分関数のf(x)と不定積分のF(x)との間で微分積分学の基本定理が成り立ちます。ただし、F(x)はx=0の点では微分できないので、x=0を変数ｘの範囲に含む場合は、F(x)とf(x)の関数の組に微分積分学の基本定理が成り立ちません。
大学数学での定義はそのようなものです。しかし、高校の数学の教科書では、関数f(x)の不定積分Ｓ（ｘ）を、f(x)の定積分に基づいて定義しないで、
関数S(x)を微分したらf(x)になった場合、
すなわち、
Ｓ’（ｘ）＝ｆ（ｘ）
となった場合に、
その原始関数S(x)が不定積分であるとして、
原始関数によって不定積分を定義しています。
そういうふうに定義した「不定積分」
（微分積分学の基本定理が成り立つように不定積分を定義した）
を、微分積分学の基本定理の「不定積分」の定義にすると、
微分積分学の基本定理の意味が不明になります。
教科書の不定積分の定義が微分積分学の基本定理そのものですので、その定義と同じ内容に見える微分積分学の基本定理を説明する意義が有りません。
しかし、「不定積分」がそのように定義されるという高校数学の微分積分の教科書の記述は嘘です。
不定積分は、正しくは、リーマン積分によって定義された定積分を基にして、定義されるのです。
教科書の積分の定義が嘘であるため、微分積分学の基本定理の存在意義があります。
そもそも、積分の概念は、日本の高校の教科書が微分の逆演算で定義しているような狭い貧弱な概念ではありません。積分の概念は、数学の研究対象を微小な部分に分割して研究し、その微小部分を集積した全体にまとめ上げて全体を考えるという、適用範囲が広い概念なのです。
高校の微分・積分の教科書は分かりにくいだけで無く、間違いも含まれています。
連続関数の定義も、高校数学の教科書で間違いを教えている。
連続関数の定義は、1817年にBolzanoが中間値の定理を証明する前提条件に連続関数の定義が必要であることを明確にしてから連続関数の定義が定まった。高校数学の連続関数の定義では、中間値の定理を成り立たせない関数を連続関数と呼んでいる。その偽物の定義に基づくと、微分積分学の基本定理を理解し難くなると考える。
読まない方が良いのではないかと考えます。高校の微分積分を勉強するなら、先ず、大学生向けの微分積分の参考書を読むことを推薦します。高校２年生が勉強するのに適切な、書店で購入できる微分積分の参考書は：
「やさしく学べる微分積分」（石村園子） ￥2000円
が内容がわかり易くて良いと思います。
この本の３６ページから４５ページまで読めば、微分の概念から始めて合成関数の微分の公式まで学ぶことができます。
高校生は、成人に成長する最終段階にいます。自ら研究して数学の独自分野を開拓する高校生もいると思います。高校生は数学の参考書を高校生向けの本に限定するこだわりは捨て、大学生向けの参考書も、自分に合っていると思えばどんどん吸収していく事が望ましいと考えます。
【微分積分学の基本定理の定義】
関数ｆ（ｘ）が、変数ｘの実数の連結区間ａ≦ｘ≦ｂ
において連続な関数である場合を考える。
すなわち、その連結区間で１つながりのグラフであるとする。
（１）
ｘ＝ａにおいてｆ（ｘ）が連続であるので、関数の連続の定義に従って、
その連結区間内で関数が連続なので、
ｘ→ａ でのｆ（ｘ）の片側極限値と、
ｘ＝ａにおける値ｆ（ａ）とが等しい。
（２）
ｘ＝ｂにおいてｆ（ｘ）が連続であるので、
ｂについても同様な関係がある。
（３）
また、関数ｆ（ｘ）が定義されている変数ｘの連結区間で関数ｆ（ｘ）が積分可能である。
そのため、その変数ｘの連結区間での積分結果の関数Ｆ（ｘ）は、その変数ｘの連結区間で値を持つ。
すなわち、積分結果の不定積分Ｆ（ｘ）は被積分関数ｆ（ｘ）と同じ連結区間のｘの定義域を持つ。
（４）
連結区間ａ≦ｘ≦ｂ
の変数ｘの範囲で定義されている不定積分Ｆ（ｘ）を微分する場合に、関数Ｆ（ｘ）の境界でも微分可能になり得るように微分の定義が修正されている。
（５）
以上で説明した定義域を持つ関数ｆ（ｘ）に関して、
不定積分Ｆ（ｘ）に関して、
連結区間ａ≦ｘ≦ｂ
の範囲のｘに関して以下の関係式が成り立つ。
Ｆ’（ｘ）＝ｆ（ｘ）
すなわち、不定積分Ｆ（ｘ）を微分して得た導関数は、元の連続関数ｆ（ｘ）（その連結区間内で連続な関数ｆ（ｘ））と一致する。
（基本定理の定義：おわり）
《微分積分学の基本定理の定義のポイント》
この基本定理の定義のポイントは、
関数ｆ（ｘ）は、もとの関数が、以下の図の様に大きな定義域の中で積分できない点がある関数であっても、その関数f(x)が、ある連結区間内で１つながりに連続である場合は、関数の定義域をその連結区間内に狭める。
その様に定義域を狭めた連結区間ａ≦ｘ≦ｂを新たな定義域にした新たな関数f(x)を考える。
このように、連結区間ａ≦ｘ≦ｂとセットにされて定義されている関数f(x)に関わる定理であるというのが第１のポイントです。
その連結区間の外の領域：
ｘ＜ａや、ｂ＜ｘ
の点で、もとの定義域の関数ｆ（ｘ）が、上図の例の様に無限大になっても良い。
元の関数ｆ（ｘ）が無限大になるという異常な領域を除外した連結区間
ａ≦ｘ≦ｂ
に限って定義された関数f(x)が定理の対象にする関数である。
その様に、区間を限定する事で、この定理を適用できる元の関数ｆ（ｘ）の選択の自由度を高くしているという特徴があります。
その様に関数ｆ（ｘ）が連続である連結区間で、ｆ（ｘ）を不定積分して、下図の関数Ｆ（ｘ）が得られます。
（注意）上図の関数ｆ（ｘ）は、ｘ＝０で不連続ですが、その連続で無い点以外の図の、関数が連続な連結区間内のｘで連続です。その連結区間内で、この関数ｆ（ｘ）が連続関数（その連結区間内で関数が連続）であると定義されます。
下図のＦ（ｘ）は、連結区間ａ≦ｘ≦ｂで定義される。
Ｆ(x)をこの連結区間で微分すれば、再び、上図の関数ｆ（ｘ）が得られます。
《下図に各種の関数の集合の包含関係をまとめた》
【問題を解く実用性に優れた形で表現した、微分積分学の基本定理】
大学１年生向けの参考書であるが、高校２年生が勉強するのに良い参考書の、「やさしく学べる微分積分」（石村園子） の１０６ページに書いてある形の、微分積分学の基本定理が、問題を解く役に立つ、実用性に優れています。
（基本定理の定義の開始）
関数ｙ＝ｆ（ｘ）が、
連結区間ａ≦ｘ≦ｂ
上で連続とする。
（連続関数の定義域は、それが連続な連結区間以上あるということは、いつも意識していて下さい）
関数ｆ（ｘ）を、それが連続する連結区間ａ≦ｘ≦ｂ
内で定積分（定積分はリーマン積分によって定義されます）することで、以下の関数Ｓ（ｘ)を求める。
すると、次のことが成り立つ。
（１）Ｓ（ｘ）はｆ（ｘ）の原始関数の１つの不定積分である。
（原始関数は、連結区間で１つながりの連続関数であり、その全区間内で微分可能な関数です。）
（２）Ｆ（ｘ）を、連結区間を定義域とするｆ（ｘ）の、その連結区間内で１つながりに連続な関数である原始関数の任意の１つとすると、
が成立する。
（定理の定義おわり）
【微分積分学の基本定理の対偶】
この定理の意味を理解するために、この定理の対偶を考えて、対偶によって定理を理解するようにします。
（基本定理の対偶（その１）の定義の開始）
とおいたとき、ある値のｃとｄで
となるならば、
関数ｙ＝ｆ（ｘ）は、
連結区間ａ≦ｘ≦ｂ のどこかで不連続である。
（対偶（その１）の定義おわり）
この対偶が成り立つだろうかと考えると、ｆ（ｘ）が不連続であっても、Ｓ(x)が計算できる（積分可能である）ならば、
とはならず、
この式の左右の辺が等しくなります。
（ここをクリックした先のページを参照）
その場合には、この式の左右の辺が等しく無いという事にはならないので、
そうなる場合にどうなるかという話自体が意味を失います。
このことによって、この定理の対偶（その１）が成立し得ると考えたことが、意味の無い事を考える間違いであり、それでは、この定理を正しく理解していなかったことが分かりました。
再度、この定理を正しく理解したと言える、定理の対偶を考えます。
（基本定理の対偶（その２）の定義の開始）
とおいたとき、ある値のｃとｄで
という計算をすることができない場合は、
が計算できず、また、関数ｙ＝ｆ（ｘ）は、
連結区間ａ≦ｘ≦ｂ のどこかで不連続である。
（対偶（その２）の定義おわり）
すなわち、この対偶（その２）は、連続で無い点を含む連結区間では積分できないことがあると言う命題です。
この命題は意味を持ちます。
意味のある対偶が考えられたので、対偶の元になった定理も、そのように解釈すべきです。
（基本定理の正しい定義の開始）
関数ｙ＝ｆ（ｘ）が、
連結区間ａ≦ｘ≦ｂ
上で１つながりに連続とする。
その条件が成り立つならば、必ず、
という不定積分Ｓ（ｘ）を計算をすることができる。
そして、次のことが成り立つ。
（１）不定積分Ｓ（ｘ）はｆ（ｘ）の原始関数の１つである。
（原始関数は、連結区間で１つながりの連続関数であり、その全区間内で微分可能な関数です。）
（２）Ｆ（ｘ）を、連結区間を定義域とするｆ（ｘ）の、その連結区間内で１つながりに連続な関数である原始関数の任意の１つとすると、
が成立する。
（定理の定義おわり）
すなわち、基本定理の意味は、その定理の命題が、Ｓ（ｘ）の式の積分計算を可能にする十分条件（関数ｆ（ｘ）が連結区間で１つながりに連続である）を述べたものであることがわかります。
この基本定理の命題が正しいか否かは、連続関数（その連結区間内で関数が１つながりに連続）が、「関数の積分を可能にする十分条件」になるか否かによって決まる。
------（補足）-------
無料でダウンロードできる大学生向けの微分積分の教科書：
「微分積分学入門」（横田 壽）
（注：横田教授が芝浦工業大学を退官したため、この教科書を無料で掲載するWebページが無くなりました。この本は書店で購入できます。）
の１１８ページ（１２５枚目）にも、
微分積分学の基本定理の証明を、
「定理3.7 f(x) が連結した閉区間[a, b] で連続ならば， [a, b] で積分可能である．」
の説明から始めています。
-----補足おわり---------
（注意）
連結区間で定義された連続な関数f(x)
に対して、
１つの原始関数S(x)が求められた場合に、
その他の全ての原始関数F(x)は、
積分定数Cを用いて、
S(x)+C,
とあらわされる事が、
以下の補助定理を利用して証明できる。
（補助定理）
ある連結区間内の実数全てのｘで定義されていて、
その連結区間の全てで微分可能であり、
F'(x)=f(x)
である、原始関数F(x)があるものとする。
被積分関数f(x)が、その連結区間においていつでも０である：
f(x)=0
ならば、
その連結区間で、
F(x)=C
である。
（定理おわり）
（証明）
この補助定理の厳密な証明は、平均値の定理を使って証明します。
しかし、高校生に有りがちな、平均値の定理を証明しないで（証明を知らないで）使うのは関心しません。そういうやり方は他人任せであり、自分では（平均値の定理の証明も含めた）証明の全貌が把握できず、数学センスに反します。
ここでは、平均値の定理の証明を知らない読者のために、
平均値の定理を使わない以下の方法で証明します。
（証明開始）
F’(x)=0なので、
微分の定義から、
(F(x+Δ)－ F(x))/Δ＝０,
(F(x+２Δ)－ F(x＋Δ))/Δ＝０,
ゆえに、F(x+2Δ)＝F(x+Δ)＝F(x),
この操作を続けると、
F(x)が微分可能なxの連結区間内では、
F(x)の値は一定値であって、
F(x)=C,
とあらわされる。
（証明おわり）
補足：
上の証明で、
F(x+2Δ)＝F(x+Δ)＝F(x)
とする操作が続けられるのは、
F(x)が微分可能なxの連結区間内に限られ、
F(x)が微分できない点でこの操作が止まる。
よって、
F(x)=C
とあらわせるｘの範囲は、
F(x)が微分可能なxの連結区間内、
すなわち、
f(x)が定義されるｘの連結区間内
に限られている。
（注意）
この補助定理のF(x)として、定数では無いカントール関数も、ほとんどの点で微分係数が０なので、使えるのでは無いかと考えるのは誤りです。
なぜならば、カントール関数は、微分不可能な点が無数にあるので、
「その導関数f(x)が連結区間においていつも０である」
という条件が成り立っていないからです。
（補助定理の利用）
この補助定理のF(x)を、
（原始関数F(x)－S(x)）
であると考えると、
原始関数F(x)は、
積分定数Cを用いて、
S(x)+C,
とあらわすことができる。
（微分積分学の基本定理の確認その１）
関数f(x)が、以下の図の様に、連結区間内で１つながりに連続な場合は、その連結区間内で関数f(x)が積分可能である。
（定理の確認その２）
一方、以下の図の様に、関数f(x)が１つながりにならず不連続になる連結区間では、関数f(x)の積分が不可能になる場合がある。
そのため、微分積分学の基本定理が成り立っている、ということがわかります。
【基本定理の証明の前半】
この微分積分学の基本定理の証明は、「やさしく学べる微分積分」（石村園子）の１０６ページの証明を読んで欲しい。
その証明の前半（１）において、
関数ｙ＝ｆ（ｘ）が、
連結区間ａ≦ｘ≦ｂ
上で１つながりに連続とする。
その条件が成り立つならば、必ず、
という計算をすることができる（f(t)が積分可能である） 。
という命題が正しい事は、以下の様にして証明できる。
（第１の証明）
この、「微分積分学の基本定理の要である」積分可能性の証明は、以下では証明の概要のみを説明します。完全な証明は、大学で学ぶ微分積分学から学んでください。完全な証明が行えるためのキーワードは、一様連続性です。
（証明の概要の説明開始）
閉区間で連続な関数は一様連続です（先ず、一様連続性の証明が必要）。すなわち、この関数f(x)をリーマン積分によって、積分区間を均等な微小領域の要素に分割した時に、分割数を多くすると、どの分割部分の微小領域内の関数値のばらつきも、一斉に小さくできる（これを一様連続と言う）。そのため閉区間で連続な関数は、分割数を多くして、一斉に、分割された微小領域内の関数値のバラツキを小さくできるので、積分の値のバラツキを小さくでき、リーマン積分可能です。
すなわち、リーマン積分で分割数を無限大にした極限で、f(x)の値を集積した値が収束する。
よって、f(x)の値を集積した関数Ｓ(x)が計算できる。
（第１の証明おわり）
（極限では無限大に発散する点（その点には接続していないが）に向けて連続している（開区間で）連続な関数は、その開区間の領域をいくら細かな微小領域に分割しても、無限大に発散する点の近傍の微小領域内の関数値のバラツキは大きい（バラツキが無限大）です。分割して作った全ての微小領域内の関数の値のバラツキを一斉に小さくできない（一様連続で無い）関数は、積分可能ではありません。）
（第２の証明）
ｆ(x)が連結な閉区間ａ≦ｘ≦ｂで１つながりに連続な関数であれば、閉区間で連続な関数の最大値・最小値の定理によって、ｆ(x)の値はある最大値と最小値の間の値に限られている。
そのように、ある最大値と最小値の間の値に限られている、閉区間で連続な関数ｆ（ｘ）の領域を以下の図の様に２等分する。
（ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。）
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ２を抽出する。
関数ｆ（ｘ）が連続関数の場合は、その差の最大値Δ２は、分割前の領域での関数の最大値と最小値の差Δ１よりも小さくなる。
更に、各領域を２等分する。
（ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。）
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ３を抽出する。
関数ｆ（ｘ）が連続関数の場合は、その差の最大値Δ３は、分割前の領域での差の最大値Δ２よりも小さくなる。
更に、各領域を２等分する操作を繰り返し、
差の最大値Δ４、Δ５、Δ６・・・
を求めて行く。
すると、関数ｆ（ｘ）が連続関数の場合は、領域を分割する毎に、全分割領域での差の最大値Δｎは無限に小さくなって行く。
（もし関数の最大値と最小値の差Δｎが無限に小さくならない点があったならば、その点は連続では無い点である。連続関数ｆ（ｘ）には、そのような点は無い。）
（一様連続性）
以上の様に、ある関数f(x)の各分割領域を更に２分の１に分割する操作をｎ回繰り返していき、各分割領域の関数f(x)の最大値と最小値の差（関数の値のばらつき）Δを求める。
（１）そのとき、全ての分割領域での関数の値のばらつきΔの最大値Δｎが有限の値で存在すること。
（２）この操作を繰り返して分割領域を無限に小さくすると、
全ての分割領域での関数の値のばらつきの最大値Δnが、無限に小さくなって行く。
（すなわち、全ての分割領域での関数の値のばらつきがΔnより小さく、そのΔnが無限に小さくなっていく）
これが成り立つ関数f(x)の性質を「一様連続」であると言います。
この説明は、以下の様に定義されている一様連続の言い換えです。
「どんなに小さな正の値εについても、全ての分割領域での関数の値のばらつきがε以下にできる、分割領域の小さな幅δ＝(b-a)/(２^n)が存在するとき、その関数は一様連続である。」
（一様連続の説明おわり）
その様に無限に小さい関数値のばらつきΔｎによる、関数ｆ（ｘ）の値の総和（リーマン積分）への影響は無限に小さい。そのため、この関数ｆ（ｘ）はリーマン積分可能である。
（第２の証明おわり）
これらの証明の様に、「関数ｆ（ｘ）が連結な閉区間ａ≦ｘ≦ｂで１つながりに連続な関数であれば、
式Ｓ(x)であらわす、リーマン積分で計算する定積分が可能である。」
（微分積分学の基本定理の証明の前半（１）おわり）
（注意）
この被積分関数のf(x)として、異常な関数であるカントール関数も、１つながりに連続な連続関数なので、使えます。
【基本定理の中段の証明】（１）
（１）不定積分Ｓ（ｘ）はｆ（ｘ）の原始関数の１つである。
（原始関数は、連結区間で１つながりの連続関数であり、その全区間内で微分可能な関数です。）
（以上が中段）
（証明開始）
この不定積分S(x)については、
正の値Δが０に近付く極限において、
S(x+Δ）－S(x)＝(f(x＋Δ/n)+f(x＋2Δ/n)+・・・+f(x＋nΔ/n))・(Δ/n)
とあらわせるので、
f(x＋Δ/n),f(x＋2Δ/n)・・・f(x＋nΔ/n)の平均値Mは、
M＝(f(x＋Δ/n)+f(x＋2Δ/n)+・・+f(x＋nΔ/n))／n＝(S(x+Δ)－S(x))／Δ
とあらわせる。
f(x)が少なくとも区間[x,x+Δ]で１つながりに連続な連続関数ならば、
正の値Δが０に近い極限では、f(x)からf(x＋nΔ/n)までの値の全てがほとんど同じ値になる。そして、
f(x＋Δ/n),f(x＋2Δ/n)・・・f(x＋nΔ/n)の平均値Mも、
f(x)とほとんど同じ値になる。
Δ→０の極限で、
(S(x+Δ)－S(x))／Δ＝M→f(x)
となる。
同様にして、Δ→０の極限で、
(S(x)－S(x－Δ))／Δ＝M→f(x)
となる。
これは、 S(x）の左側微分係数と右側微分係数が等しくf(x)になる事を意味する。
よって、S(x)は微分可能であって、その導関数がf(x)になる。
よって、
S(x)はf(x)の原始関数の１つである。
（中段の証明おわり）
【微分積分学の基本定理の後半（２）】
（２）Ｆ（ｘ）を、連結区間を定義域とするｆ（ｘ）の、その連結区間内で１つながりに連続な関数である原始関数の任意の１つとすると、
が成立する。
微分積分学の基本定理の後半（２）が成り立つ事は、以下の様にして証明できる。
（証明開始）
リーマン積分によって、微小領域の要素に分割して集積する積分Ｆ(x)の値の、分割数を無限大にする極限の値が計算できる場合は、
すなわち、微小領域の要素を集積する区間を分割して、
その分割した区間毎の要素の集積値の極限値を求める事ができる場合は：
リーマン積分の積分範囲の区間を、２の区間ＡとＢに分割して、
区間Ａでの要素の集積値の極限値＋区間Ｂでの要素の集積値の極限値＝区間Ａと区間Ｂを合わせた区間での要素の集積値の極限値
になる。
ゆえに、微分積分学の基本定理の証明の後半（２）が成り立つ。
（証明おわり）
「やさしく学べる微分積分」（石村園子）の１０６ページの形の微分積分学の基本定理を使うと、以下の定理がすぐに導き出せる。
【定理】
連結区間ａ≦ｘ≦ｂ
の範囲で１つながりに連続な関数ｆ（ｘ）がある場合：
連結区間ａ＜ｘ＜ｂ
の範囲で、
ｆ（ｘ）＞０
ならば、
連結区間ａ≦ｘ≦ｂの範囲で、
ｆ（ｘ）の不定積分Ｆ（ｘ）は単調増加である。
（定理の定義おわり）
（証明開始）
関数ｆ（ｘ）が
連結区間ａ≦ｘ≦ｂ
で連続であるので、
ａ≦ｘ１＜ｘ２≦ｂ
なるｘ１とｘ２に関して、
微分積分学の基本定理により、
よって、
Ｆ（ｘ）は単調増加である。
（証明おわり）
以下の定理があります。
【定理】
連結区間ａ≦ｘ≦ｂ
の範囲で連続な関数Ｆ（ｘ）がある場合：
連結区間ａ＜ｘ＜ｂ
の範囲で、
Ｆ’（ｘ）≡ｆ（ｘ）＞０
ならば、
ａ≦ｘ≦ｂの範囲で、
関数Ｆ（ｘ）は単調増加である。
（定理の定義おわり）
平均値の定理を使って、この定理を証明しておきます。
（証明開始）
連結区間ａ≦ｘ≦ｂ
の範囲で連続な関数Ｆ（ｘ）が：
連結区間ａ＜ｘ＜ｂ
の範囲で微分可能で、
Ｆ’（ｘ）＝ｆ（ｘ）
の場合、
平均値の定理によって、
ａ≦ｘ１＜ｘ２≦ｂ
なるｘ１とｘ２に関して、
（Ｆ（ｘ２）－Ｆ（ｘ１））／（ｘ２－ｘ１）＝ｆ（ｘ）
となるｘが、
ａ≦ｘ１＜ｘ＜ｘ２≦ｂ
に、少なくとも１つ存在する。
その範囲で、
ｆ（ｘ）＞０
なので、
Ｆ（ｘ２）＞Ｆ（ｘ１）
である。
よって、Ｆ（ｘ）は単調増加である。
（証明おわり）
《微分と積分の関係》
なお、全ての種類の関数における、積分前の関数ｆ（ｘ）と、微分前の関数Ｆ（ｘ）との、変数ｘの一部の定義域での微分積分のあり得る関係が以下の図であらわせます。
（なお、Ｆ（ｘ）として考えられる関数の、関数が連続な領域内の至るところ微分不可能な関数であるワイエルシュトラス関数等は、連続で無い点を持たないが、微分不可能です。）
（上図で、関数ｆ２（ｘ）は、除去可能な連続で無い点を除去した関数です。関数Ｆ（ｘ）は、関数Ｆ（ｘ）の連続で無い点を除いた変数ｘの範囲でｆ（ｘ）の不定積分であるとともに、ｆ２（ｘ）の不定積分でもあります）
上図の、ｆ（ｘ３）とＦ（ｘ３）の関数のセットの例：
以下で定義する関数のセットでは、ｆ（ｘ）にｘ＝ｘ３で除去不可能な連続で無い点があって、ｆ（ｘ）は不連続な関数（その点で関数が不連続な関数であって、その点以外の領域では関数が連続な連続関数である）です。
しかし、この連続で無い点を持つ関数ｆ（ｘ）を、その連続で無い点を含む連結区間で定積分することで定義した関数Ｆ（ｘ）が、その連続で無い点の位置ｘ３でも変数ｘで微分可能で、Ｆ（ｘ）を微分すると再び連続で無い点を持つｆ（ｘ）が得られます。
（Ｆ（ｘ）の定義）
ｘ≠０の場合：
ｘ＝０の場合： Ｆ（０）＝０，
（導関数ｆ（ｘ））
この関数Ｆ（ｘ）はｘ≠０の場合も、ｘ＝０の場合も、微分可能で、
その導関数ｆ（ｘ）は、以下の式であらわせます。
ｘ≠０の場合の微分：
になり、ｘが０に近づくとー１と１の間を振動します。
この導関数が含むｃｏｓ（１／ｘ）の関数が以下のグラフであらわす形の関数になるからです。
Ｘ＝０の場合にも、Ｆ（ｘ）は微分可能で：
というように、０になります。
そのため、この導関数ｆ（ｘ）は、ｘ＝０で連続ではありませんが、Ｆ（ｘ）を微分することで得られます。
この導関数ｆ（ｘ）は積分可能であり、積分するとＦ（ｘ）になります。
この関数Ｆ（ｘ)はｘ＝０で連続な関数です。
この様な複雑な関係の中から、比較的に扱い易い連続関数（連結区間内で関数が１つながりに連続）を使って従来の微分積分学の基本定理が定められています。
また、大学以上の微分積分学では、積分の定義をどんどん拡張して、何でも積分できるようにして、ある関数ｆ（ｘ）を積分して連続で無い点を持つ関数Ｆ（ｘ)を得ることができるようにし、その連続で無い点を持つ関数Ｆ（ｘ)を微分して関数ｆ（ｘ）を得ることができるように、微分の定義も拡張するというような事も行なわれます。
そのように微分・積分の定義を拡張する入口に、微分積分の基本定理が置かれています。
そのため、微分積分学の基本定理の：
という式の意味することは：
この公式の前提条件以外の条件によってこの式と異なる結果が得られるわけでは無く、
この式を成り立たせるように、ｆ（ｘ）とＦ（ｘ）を対応させる規則である微分と積分とを矛盾が生じ無い様に定義を修正して、この式を成り立たせているのです。
微分積分学の基本定理の登場により我々に注意が喚起されたメッセージは、
『関数ｆ（ｘ）の積分を計算しようとする場合には、その積分区間における関数の性質（連続である等）を調べなければならない』
というメッセージです。
原始関数を用いて定積分を計算する演算の際に、その定積分の積分区間における関数の性質を調べる事を欠かしてはならない、というメッセージです。
この大切なメッセージについては、日本の高校の積分の授業では、「積分する区間内の全ての変数値に対して関数値が定義されていなければならない」と教えられているようです。先ず、それは必要です。しかし、それだけでは十分ではありません。
そして、高校で習う、
「原始関数Ｆ（ｘ）を使って、以下の計算で定積分する。」
に従って計算すると、以下の例の様に、
複合区間を定義域にする高校数学の誤った原始関数Ｆ(x)を使った計算では元の関数のグラフの面積が計算できず、
間違った答えになります。
以下の様に、関数ｆ（ｘ）の連続で無い点を定積分の連結区間内に入れてしまうと以下の間違いをおかします。
Ｆ（ｘ）＝１／ｘをｘで微分したらｆ（ｘ）＝－１／ｘ２になるので、関数ｆ（ｘ）＝－１／ｘ２の原始関数がＦ（ｘ）＝１／ｘであると誤解します。
（原始関数は連結区間で１つながりに連続な関数です）
しかし、積分区間を、ｆ（ｘ）が不連続になる変数値ｘ＝０を含めた、ｘが－１から１までの区間にして、
関数ｆ（ｘ）を定積分しようとして、
複合区間を定義域にする誤った原始関数Ｆ（ｘ）を使って、
Ｆ（１）－Ｆ（－１）＝１－（－１）＝２
という 計算をすると、明らかに間違えます。
上の図で明らかな様に、－１から１までの範囲でのｆ（ｘ）の積分の結果は（積分がグラフの面積を表すので）、マイナス無限大にならなければなりません。
しかし、上の計算はそれと全く違う、間違った答えになったのが明らかです。
微分積分学の基本定理によって、
原始関数F(x)を使って被積分関数ｆ（ｘ）の定積分が計算できる事が完全に保証されているのは、ｆ（ｘ）が、その積分区間で連続なときだけです。
それ以外の場合には、その計算の答えが間違っていることがある、という事を認識しなければなりません。
（複合区間を定義域にする誤った原始関数の差で計算するから間違えるのであって、不定積分（必ず連続関数になる）の差で定積分を計算するならば、間違いは起きません。不定積分（いつも連続関数）の差で定積分を求めたと書く答案が一番正しい答案だと思います。）
また、
という計算で得た関数S(x)は不定積分であって、連結区間内で１つながりに連続な関数です。
実際、ａ＞０の場合には、ｘ＞０の範囲の定義域だけの関数
Ｓ（ｘ）＝１／ｘ， （ｘ＞０）
だけが得られます。
ａ≦ｂ＜０の場合には、ｘ＜０の範囲の定義域だけの関数
Ｓ（ｘ）＝１／ｘ， （ｘ＜０）
だけが得られます。
ａ＝０の場合には、ｓ（ｘ）が計算できません。
このように、
不定積分：
は、
定義域がｘ＜０とｘ＞０との両方の領域を含む関数という複合区間を定義域にする誤った原始関数：
ｘ≠０における
Ｆ（ｘ）＝１／ｘ， （ｘ≠０）
とは異なります。
（もう１つの注意）
以下の関数ｆ（ｘ）は関数の定義域内の全ての点で連続ですが、１つながりに連続な関数では無いので連続関数ではありません。
高校教科書の誤った連続関数の定義：「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である。」に従うと、これを連続関数とする誤りに陥ります。
《高校数学の「微分積分学の基本定理」の定義》
以下でこの微分積分学の基本定理を考察する。
この切れ切れのノコギリ状の関数ｆ（ｘ）を不定積分した関数Ｓ(x)＝Ｆ（ｘ）を求めてみます。
この関数Ｓ(x)＝Ｆ（ｘ）を微分すると、ｘ＝0.5, 1.5, 2.5等では、Ｓ(x)＝Ｆ（ｘ）の微分係数が計算できません。
この関数Ｓ(x)＝Ｆ（ｘ）は原始関数ではありません。
そうなる原因は、被積分関数ｆ（ｘ）が１つながりに連続では無いので連続関数では無かったから、
微分積分学の基本定理の前提条件である、
「関数ｙ＝ｆ（ｘ）が、連結区間ａ≦ｘ≦ｂの全ての点で連続である」
条件が成り立っていなかったからです。
正しい連続関数の定義に従うと、
「（被積分関数ｆ(x)を連続関数に限定すると）微分と積分が逆演算になる」
と要約した、この微分積分学の基本定理が成り立つ事が言えます。
しかし、高校教科書の誤った連続関数の定義：「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である。」に従うと、
上の事例が、
「（被積分関数ｆ(x)を（正しい定義の）連続関数に限定すると）微分と積分が逆演算になる」
と要約した、この微分積分学の基本定理の反例になっていると誤解しますので、注意する必要があります。
《微分積分学の基本定理の拡張》
なお、微分積分学の基本定理が積分可能性を完全に保証する条件であるｆ（ｘ）が積分区間で連続でなければならないという条件は、緩める事ができ、
ｆ（ｘ）の不定積分Ｆ（ｘ）が積分区間で連続であるだけで良いということが分かっています。
それは、
数学者の藤原松三郎の「微分積分学 第１巻」が、
不連続関数ｆ（ｘ）の積分を広義積分と呼び、
その積分において、関数ｆ（ｘ）の積分区間
ａ≦ｘ≦ｂ
内で連続な不定積分F(x)が得られたら、
（その積分区間内のｘで、ｆ(x)が微分不可能な点があっても良く）
（１）それは、不連続関数ｆ（ｘ）が積分可能である証拠であり、
（２）不定積分F(x)を使った以下の計算で定積分を計算して良い事が書いてあります。
Ｆ（ｂ）－Ｆ（ａ）
そのため、定積分が可能な積分区間の判定条件を緩めることができ、
不連続な関数ｆ（ｘ）に対して、
その積分区間で連続な１つながりの不定積分Ｆ（ｘ）が見つかったなら、
その不定積分Ｆ（ｘ）を使ってその区間の定積分を計算して良いです。
また、小寺平治・著「はじめての微分積分15講」（2,200円）の１０３ページにも、このことが書いてあります。
（複合区間を定義域にする誤った原始関数の差で計算するから間違えるのであって、不定積分（必ず正しい定義の連続関数になる）の差で定積分を計算するならば、間違いは起きません。不定積分（いつも（正しい定義の）連続関数になる）の差で定積分を求めたと書く答案が一番正しい答案だと思います。）
【ここをクリックした先に、まぼろしの基本定理があります】
リンク：
高校数学の目次
上の式１の３次関数のグラフの点Ａでの接線と点Ｂでの接線の交点をＰとする。交点Ｐを通って式１の曲線に点Ｃで接する第３の接線ＰＣを考える。
