

(ページ内リンク先)
▽基本定理の概要
▽微分積分学の基本定理の定義
▽基本定理の定義のポイント
▽基本定理の対偶
▽微分積分学の基本定理の正しい定義
▽補助定理
▽基本定理の確認
▽基本定理の前半の証明
▽基本定理の中段の証明
▽基本定理の後半の証明
▽微分と積分の関係
▽微分積分学の基本定理の拡張
《基本定理の概要》
【被積分関数の単位】
被積分関数は、均質な基本的な要素の単位で考える。
具体的には、被積分関数を、全て、1つながりに連続する関数を単位にして考える。1つながりに連続する関数は正しく定義された連続関数です。その、1つながりに連続する関数を扱うのであれば、積分の計算で誤りに陥る事を防ぐことができます。
(微分型の)《微分積分学の基本定理》
微分型で表現した微分積分学の基本定理は:
連結区間内で1つながりに連続な関数f(x)がある場合:

が成り立つというものです。
高校の微分積分の教科書では、この定理が当然に成り立つものとして、証明しないで使っています。
(高校の微分積分の参考書に以下の証明があります)
「駿台受験シリーズ 分野別 受験数学の理論7 微分法・積分法の基礎」
https://math.co.jp/contpgm2/w_main.php?oya_id=2&back_id=14#14
(96ページ途中から)



《補足》(この証明での重要ポイント)
以上の証明の中で、関数f(x)がx軸上のxの点において連続関数であるという前提条件を使っている。つまり、関数f(x)が連続関数なので、hを十分小さくすれば、f(x+h)がf(x)に近づく、という前提条件を使った。
この証明の発想の根底に、関数(グラフ)が連続であるという概念が、証明の重要なポイントになっているということに気づくことが大事だ。そこから、連続関数の性質を深く研究する、という数学の研究の焦点が絞られ、その研究の成果が、数学における極限の概念の確立などだろう。
古典的(基礎的)微分積分学を教える高木貞治の「解析概論」では、連続関数を、「ある区域(区間)内において,変数xが連続的に変動するのに伴って連続的に変動する関数f(x) 」と呼んでいる。関数f(x) が連続的に変動するという意味は、関数が区間で、連続的に定義されているという意味である。すなわち、f(x)=1/x という関数のように、x=ー1からx<0までは関数f(x) が定義されていて、x=0では関数が定義されていない。再びx>0からx=1まで関数f(x) が定義されている。といった、関数が区間[-1,1]で連続的には定義されていない関数は連続関数ではないのである。
そういう、数学の根底の思想が、大学の微分積分学によって学ぶことができるハズだった。しかし、最近の大学数学では、微分積分の基礎(微分積分学の根底の思想)は高校で学んできたハズ、として、いきなり、現代数学(位相空間論)の微分積分学から教えるようになっているようです。そういう状況なので、古典的な(基礎的な)微分積分の概念は、自力でしっかり学ぶしかないようです。 ここをクリックした先の「連続関数とは何か」のサイトから、微分積分の基礎の概念を学んでください。
微分積分の高校数学での参考書にも、以上の(駿台の受験シリーズの)参考書のように、数学の発想の礎を作るために良い参考書があった。
一方、高校の微分積分の教科書は偽物で、数学の発想の基礎作りに役立たないと考える。
(補足おわり)

この式が成り立たない場合などあり得ないのではないか?と考える人もいるかもしれません。
この式が成り立たない場合というのは、f(x)が積分出来ない場合です。そもそも積分できなければ、微分する以前に、この式が成り立たないことになります。
また、f(x)が積分して関数F(x)が得られても、関数F(x)が折れ曲がった関数になれば、その折れ曲がり点でF(x)は微分できません。F(x)が微分できなければ、この式が成り立たないことになります。
「関数 f(x) が連結区間内で1つながりに連続している関数f(x)が積分可能である。その積分結果の関数F(x)が、その連結区間で微分可能である。そうして微分した結果は元の関数f(x)に戻る。」というのが(微分型の)微分積分学の基本定理です。
そこには、「関数 f(x) が、ある連結区間内で1つながりに連続している」という条件が付いているのです。
ーー【区間の定義】ーー
「区間」という数学用語は、変数xの数直線上の1つの範囲内の、実数のすき間がない1かたまりの数の集合をあらわす数学用語である。
《神奈川大学》【定義 14.2.4.】
a, b を実数とする. a 以上かつ b 以下の実数をすべて集めた集合を [a, b] と書き, これを閉区 間と呼ぶ.
a より大きくかつ b 未満の実数をすべて集めた集合を (a, b) と書き, これを開区間と呼ぶ.
----定義おわり----
a≦x≦bを満足するxの区間という表現は、a≦x≦bの範囲内の全ての実数xという意味です。
-∞<x<∞という区間もあります。
区間はxの値の範囲を限定するためのa≦x≦bという式とは意味が異なることに注意する必要があります。
「区間」という用語は、特に重要な関数である連続関数の連続性を定義するために必要な、連続関数f(x)の変数xの集合体がいつも持っていなければならない連続性という重要な性質が「区間」という概念を用いてあらわされています。
すなわち、変数xの「区間」の性質で大切なのは、
「区間」のなかに変数xの値が隙間なく存在すること。
つまり所定範囲内での隙間が無い全ての実数の集合という概念が「区間」という用語で定義されています。
例えば:
f(x)=1/xの定義域を(0,∞) (={x|xは0より大きい実数})
とすれば、f(x)は区間で定義された関数です。
g(x)=1/xの定義域を(-∞,0)∪(0,∞)(={x|xは0でない実数})
とすれば、g(x)は区間で定義された関数ではない。
(f(x)とg(x)は定義域が異なっているため、f(x)とg(x)は同じ関数ではない)
(積分型の)《微分積分学の基本定理》
先ず、以下の注意をしておきます。
【注意:間違った計算の例】
以下の図の関数F(x)を考える。

F(x)=C2, (x<0)
F(x)=C1, (x>0)
例えば、C1=1, C2=2, とする。
この関数F(x)を微分して積分してみます。
先ず、微分します。
F'(x)= f(x)=0, (x≠0)
次に、このf(x)を積分します。
ここで、関数f(x)が、変数xが定義される範囲が、連結区間内の全ての実数であること。その連結区間内の全ての実数の変数xで関数f(x)が定義されていなければ、その関数は(変数xの定義域とセットになっているのが関数です)積分してはいけません。
f(x)=0, (x>0) は積分できます。
f(x)=0, (x<0) も積分できます。
しかし、
f(x)=0, (x≠0) は、x≠0 の範囲でx=0の点ではf(x)が定義されていないので、その点をまたいで積分してはいけません。
もし、それを無視して無理に積分すると、
∫F'(x)dx=∫0dx=C, x≠0,
という積分になりますが、
その結果の積分定数Cをどのような値に調整しても、それは、元の関数F(x)には決してなりません。
(「元の関数F(x), (x≠0) は、変数xで関数F(x)が定義されるxの範囲が、x=0が除外されていることで、そのxの範囲(定義域)が、連結区間内の全ての実数では無い関数でした。)
以下で、(積分型の)微分積分学の基本定理を説明します。
(1)関数f(x)を、それが連続する連結区間a≦x≦b
内で定積分(定積分はリーマン積分によって定義されます)することで関数S(x)を求めます。
その関数をxの関数(不定積分)として求めます。
その不定積分は、定積分の計算を実行する苦労をして得た結果を元にして求めます。
(2)一方で、1つながりに連続で、かつ、微分可能な関数F(x)があって、そのF(x)を微分して求めた導関数がf(x)と一致するならば、その関数F(x)がS(x)と一致する。すなわち、S(x)はf(x)の原始関数の1つである。そして、そのF(x)について、
が成立する。というのが微分積分学の基本定理です。
すなわち、そのF(x)が、苦労して求めるべき不定積分S(x)と一致することが分かりました。
そのF(x)を原始関数と名付け、
その原始関数F(x)を使うことにより計算がとても楽になったので 感動した!
という内容が、(積分型の)微分積分学の基本定理です。
-----【原始関数の正しい定義】---------------
(原始関数の正しい定義は、1つながりに連続で、かつ、微分可能な関数F(x)をf(x)の原始関数と定義します)
すなわち、関数F(x)が、連結区間a<x<bのどの点でも連続、かつ、微分可能な関数であれば、F(x)を微分して導関数f(x)が求められる。この場合に、F(x)を関数f(x)の原始関数と言う。
(藤原松三郎の「微分積分学 第1巻」)
すなわち、原始関数は連結区間における連続関数であり1つながりのグラフであると定義されています。
-------原始関数の定義おわり-----------------
(微分可能の定義との関係)あと、微分積分学の基本定理の根底を支えているのが微分可能の定義です。高校数学では、微分可能の定義として、関数が定義される区間の内点(境界点以外の点)が微分可能な場合に右微分係数と左微分係数が一致するとする微分可能の条件しか教えられていません。
変数xの閉区間(a≦x≦b)で定義された関数f(x)の閉区間の境界点=端点でも、片側微分係数があれば、端点でも微分可能です。
大学数学では、変数xが閉区間(a≦x≦b)で定義された関数f(x)の区間の端点x=a,bでも、片側微分係数があるだけで微分可能とする微分可能の定義が詳しく教えられます。そのため、大学数学になって初めて、閉区間で定義された関数f(x)にも微分積分学の基本定理が成り立つことが正しく理解できます。
上図の関数f(x)と、下図の関数F(x)の間では、定義域がx>0での被積分関数のf(x)と不定積分のF(x)との間で微分積分学の基本定理が成り立ちます。ただし、F(x)はx=0の点では微分できないので、x=0を変数xの範囲に含む場合は、F(x)とf(x)の関数の組に微分積分学の基本定理が成り立ちません。
大学数学での定義はそのようなものです。しかし、高校の数学の教科書では、関数f(x)の不定積分S(x)を、f(x)の定積分に基づいて定義しないで、
関数S(x)を微分したらf(x)になった場合、
すなわち、
S’(x)=f(x)
となった場合に、
その原始関数S(x)が不定積分であるとして、
原始関数によって不定積分を定義しています。
そういうふうに定義した「不定積分」
(微分積分学の基本定理が成り立つように不定積分を定義した)
を、微分積分学の基本定理の「不定積分」の定義にすると、
微分積分学の基本定理の意味が不明になります。
教科書の不定積分の定義が微分積分学の基本定理そのものですので、その定義と同じ内容に見える微分積分学の基本定理を説明する意義が有りません。
しかし、「不定積分」がそのように定義されるという高校数学の微分積分の教科書の記述は嘘です。
不定積分は、正しくは、リーマン積分によって定義された定積分を基にして、定義されるのです。
教科書の積分の定義が嘘であるため、微分積分学の基本定理の存在意義があります。
そもそも、積分の概念は、日本の高校の教科書が微分の逆演算で定義しているような狭い貧弱な概念ではありません。積分の概念は、数学の研究対象を微小な部分に分割して研究し、その微小部分を集積した全体にまとめ上げて全体を考えるという、適用範囲が広い概念なのです。
高校数学の微分・積分の教科書は分かりにくいだけで無く、間違いも含まれています。
連続関数の定義は、1817年にBolzanoが中間値の定理を証明する前提条件に定義した連続関数の定義により、歴史上初めて連続関数が正しく定義された(その定義は関数の連続性を区間で定義するものである)。
高校数学の微分積分の教科書で定義する「連続関数」は1817年にBolzanoが定義した連続関数とは異なる定義である。
その偽物の定義に基づくと、微分積分学の基本定理を理解し難くなると考える。
日本の大学数学では、1817年にBolzanoが定義した連続関数を、「区間で連続な関数」と呼んでいる。
関数の連続性に係る定理には、必ず「区間で連続な関数」という言葉が使われる。
高校数学の偽物の「連続関数の定義」は読まない方が良いのではないかと考えます。
(注意1)
ただし、高校数学の数Ⅲの教科書「数学Ⅲ Advanced」(東京書籍)では、1817年にBolzanoが正しく定義した連続関数を、以下のように正しく定義している。
「関数f(x) がある区間Iに属するすべての値xで連続であるとき、f(x) は区間Iで連続である。」
そのように正しい連続関数の定義を教えている高校数学の教科書もあるので、全ての高校数学の教科書がダメというわけでもない。
高校の微分積分を勉強するなら、先ず、大学生向けの微分積分の参考書を読むことを推薦します。高校2年生が勉強するのに適切な、書店で購入できる微分積分の参考書は:
「やさしく学べる微分積分」(石村園子) ¥2000円
が内容がわかり易くて良いと思います。
この本の36ページから45ページまで読めば、微分の概念から始めて合成関数の微分の公式まで学ぶことができます。
高校生は、成人に成長する最終段階にいます。自ら研究して数学の独自分野を開拓する高校生もいると思います。高校生は数学の参考書を高校生向けの本に限定するこだわりは捨て、大学生向けの参考書も、自分に合っていると思えばどんどん吸収していく事が望ましいと考えます。
【微分積分学の基本定理の定義】
関数f(x)が、変数xの実数の連結区間a≦x≦b
において連続な関数である場合を考える。
すなわち、その連結区間で1つながりのグラフであるとする。
(1)
x=aにおいてf(x)が連続であるので、関数の連続の定義に従って、
その連結区間内で関数が連続なので、
x→a でのf(x)の片側極限値と、
x=aにおける値f(a)とが等しい。
(2)
x=bにおいてf(x)が連続であるので、
bについても同様な関係がある。
(3)
また、関数f(x)が定義されている変数xの連結区間で関数f(x)が積分可能である。
そのため、その変数xの連結区間での積分結果の関数F(x)は、その変数xの連結区間で値を持つ。
すなわち、積分結果の不定積分F(x)は被積分関数f(x)と同じ連結区間のxの定義域を持つ。
(4)
連結区間a≦x≦b
の変数xの範囲で定義されている不定積分F(x)を微分する場合に、関数F(x)の境界でも微分可能になり得るように微分の定義が修正されている。
(5)
以上で説明した定義域を持つ関数f(x)に関して、
不定積分F(x)に関して、
連結区間a≦x≦b
の範囲のxに関して以下の関係式が成り立つ。
F’(x)=f(x)
すなわち、不定積分F(x)を微分して得た導関数は、元の連続関数f(x)(その連結区間内で連続な関数f(x))と一致する。
(基本定理の定義:おわり)
《微分積分学の基本定理の定義のポイント》
この基本定理の定義のポイントは、
関数f(x)は、もとの関数が、以下の図の様に大きな定義域の中で積分できない点がある関数であっても、その関数f(x)が、ある連結区間内で1つながりに連続である場合は、関数の定義域をその連結区間内に狭める。
その様に定義域を狭めた連結区間a≦x≦bを新たな定義域にした新たな関数f(x)を考える。
このように、連結区間a≦x≦bとセットにされて定義されている関数f(x)に関わる定理であるというのが第1のポイントです。
その連結区間の外の領域:
x<aや、b<x
の点で、もとの定義域の関数f(x)が、上図の例の様に無限大になっても良い。
元の関数f(x)が無限大になるという異常な領域を除外した連結区間
a≦x≦b
に限って定義された関数f(x)が定理の対象にする関数である。
その様に、区間を限定する事で、この定理を適用できる元の関数f(x)の選択の自由度を高くしているという特徴があります。
その様に関数f(x)が連続である連結区間で、f(x)を不定積分して、下図の関数F(x)が得られます。
(注意)上図の関数f(x)は、x=0で不連続ですが、その連続で無い点以外の図の、関数が連続な連結区間内のxで連続です。その連結区間内で、この関数f(x)が連続関数(その連結区間内で関数が連続)であると定義されます。
下図のF(x)は、連結区間a≦x≦bで定義される。
F(x)をこの連結区間で微分すれば、再び、上図の関数f(x)が得られます。
《下図に各種の関数の集合の包含関係をまとめた》
【問題を解く実用性に優れた形で表現した、微分積分学の基本定理】
大学1年生向けの参考書であるが、高校2年生が勉強するのに良い参考書の、「やさしく学べる微分積分」(石村園子) の106ページに書いてある形の、微分積分学の基本定理が、問題を解く役に立つ、実用性に優れています。
(基本定理の定義の開始)
関数y=f(x)が、
連結区間a≦x≦b
上で連続とする。
(連続関数の定義域は、それが連続な連結区間以上あるということは、いつも意識していて下さい)
関数f(x)を、それが連続する連結区間a≦x≦b
内で定積分(定積分はリーマン積分によって定義されます)することで、以下の関数S(x)を求める。
すると、次のことが成り立つ。
(1)S(x)はf(x)の原始関数の1つの不定積分である。
(原始関数は、連結区間で1つながりの連続関数であり、その全区間内で微分可能な関数です。)
(2)F(x)を、連結区間を定義域とするf(x)の、その連結区間内で1つながりに連続な関数である原始関数の任意の1つとすると、
が成立する。
(定理の定義おわり)
【微分積分学の基本定理の対偶】
この定理の意味を理解するために、この定理の対偶を考えて、対偶によって定理を理解するようにします。
(基本定理の対偶(その1)の定義の開始)
とおいたとき、ある値のcとdで
となるならば、
関数y=f(x)は、
連結区間a≦x≦b のどこかで不連続である。
(対偶(その1)の定義おわり)
この対偶が成り立つだろうかと考えると、f(x)が不連続であっても、S(x)が計算できる(積分可能である)ならば、
とはならず、
この式の左右の辺が等しくなります。
(ここをクリックした先のページを参照)
その場合には、この式の左右の辺が等しく無いという事にはならないので、
そうなる場合にどうなるかという話自体が意味を失います。
このことによって、この定理の対偶(その1)が成立し得ると考えたことが、意味の無い事を考える間違いであり、それでは、この定理を正しく理解していなかったことが分かりました。
再度、この定理を正しく理解したと言える、定理の対偶を考えます。
(基本定理の対偶(その2)の定義の開始)
とおいたとき、ある値のcとdで
という計算をすることができない場合は、
が計算できず、また、関数y=f(x)は、
連結区間a≦x≦b のどこかで不連続である。
(対偶(その2)の定義おわり)
すなわち、この対偶(その2)は、連続で無い点を含む連結区間では積分できないことがあると言う命題です。
この命題は意味を持ちます。
意味のある対偶が考えられたので、対偶の元になった定理も、そのように解釈すべきです。
(基本定理の正しい定義の開始)
関数y=f(x)が、
連結区間a≦x≦b
上で1つながりに連続とする。
その条件が成り立つならば、必ず、
という不定積分S(x)を計算をすることができる。
そして、次のことが成り立つ。
(1)不定積分S(x)はf(x)の原始関数の1つである。
(原始関数は、連結区間で1つながりの連続関数であり、その全区間内で微分可能な関数です。)
(2)F(x)を、連結区間を定義域とするf(x)の、その連結区間内で1つながりに連続な関数である原始関数の任意の1つとすると、
が成立する。
(定理の定義おわり)
すなわち、基本定理の意味は、その定理の命題が、S(x)の式の積分計算を可能にする十分条件(関数f(x)が連結区間で1つながりに連続である)を述べたものであることがわかります。
この基本定理の命題が正しいか否かは、連続関数(その連結区間内で関数が1つながりに連続)が、「関数の積分を可能にする十分条件」になるか否かによって決まる。
(注意)
連結区間で定義された連続な関数f(x)
に対して、
1つの原始関数S(x)が求められた場合に、
その他の全ての原始関数F(x)は、
積分定数Cを用いて、
S(x)+C,
とあらわされる事が、
以下の補助定理を利用して証明できる。
(補助定理)
ある連結区間内の実数全てのxで定義されていて、
その連結区間の全てで微分可能であり、
F'(x)=f(x)
である、原始関数F(x)があるものとする。
被積分関数f(x)が、その連結区間においていつでも0である:
f(x)=0
ならば、
その連結区間で、
F(x)=C
である。
(定理おわり)
(証明)
この補助定理の厳密な証明は、平均値の定理を使って証明します。
しかし、高校生に有りがちな、平均値の定理を証明しないで(証明を知らないで)使うのは関心しません。そういうやり方は他人任せであり、自分では(平均値の定理の証明も含めた)証明の全貌が把握できず、数学センスに反します。
ここでは、平均値の定理の証明を知らない読者のために、
平均値の定理を使わない以下の方法で証明します。
(証明開始)
F’(x)=0なので、
微分の定義から、
(F(x+Δ)- F(x))/Δ=0,
(F(x+2Δ)- F(x+Δ))/Δ=0,
ゆえに、F(x+2Δ)=F(x+Δ)=F(x),
この操作を続けると、
F(x)が微分可能なxの連結区間内では、
F(x)の値は一定値であって、
F(x)=C,
とあらわされる。
(証明おわり)
補足:
上の証明で、
F(x+2Δ)=F(x+Δ)=F(x)
とする操作が続けられるのは、
F(x)が微分可能なxの連結区間内に限られ、
F(x)が微分できない点でこの操作が止まる。
よって、
F(x)=C
とあらわせるxの範囲は、
F(x)が微分可能なxの連結区間内、
すなわち、
f(x)が定義されるxの連結区間内
に限られている。
(注意)
この補助定理のF(x)として、定数では無いカントール関数も、ほとんどの点で微分係数が0なので、使えるのでは無いかと考えるのは誤りです。
なぜならば、カントール関数は、微分不可能な点が無数にあるので、
「その導関数f(x)が連結区間においていつも0である」
という条件が成り立っていないからです。
(補助定理の利用)
この補助定理のF(x)を、
(原始関数F(x)-S(x))
であると考えると、
原始関数F(x)は、
積分定数Cを用いて、
S(x)+C,
とあらわすことができる。
(微分積分学の基本定理の確認その1)
関数f(x)が、以下の図の様に、連結区間内で1つながりに連続な場合は、その連結区間内で関数f(x)が積分可能である。
(定理の確認その2)
一方、以下の図の様に、関数f(x)が1つながりにならず不連続になる連結区間では、関数f(x)の積分が不可能になる場合がある。
そのため、微分積分学の基本定理が成り立っている、ということがわかります。
【基本定理の証明の前半】
この微分積分学の基本定理の証明は、「やさしく学べる微分積分」(石村園子)の106ページの証明を読んで欲しい。
その証明の前半(1)において、
関数y=f(x)が、
連結区間a≦x≦b
上で1つながりに連続とする。
その条件が成り立つならば、必ず、
という計算をすることができる(f(t)が積分可能である) 。
という命題が正しい事は、以下の様にして証明できる。
(第1の証明)
この、「微分積分学の基本定理の要である」積分可能性の証明は、以下では証明の概要のみを説明します。完全な証明は、大学で学ぶ微分積分学から学んでください。完全な証明が行えるためのキーワードは、一様連続性です。
(証明の概要の説明開始)
閉区間で連続な関数は一様連続です(先ず、一様連続性の証明が必要)。すなわち、この関数f(x)をリーマン積分によって、積分区間を均等な微小領域の要素に分割した時に、分割数を多くすると、どの分割部分の微小領域内の関数値のばらつきも、一斉に小さくできる(これを一様連続と言う)。そのため閉区間で連続な関数は、分割数を多くして、一斉に、分割された微小領域内の関数値のバラツキを小さくできるので、積分の値のバラツキを小さくでき、リーマン積分可能です。
すなわち、リーマン積分で分割数を無限大にした極限で、f(x)の値を集積した値が収束する。
よって、f(x)の値を集積した関数S(x)が計算できる。
(第1の証明おわり)
(極限では無限大に発散する点(その点には接続していないが)に向けて連続している(開区間で)連続な関数は、その開区間の領域をいくら細かな微小領域に分割しても、無限大に発散する点の近傍の微小領域内の関数値のバラツキは大きい(バラツキが無限大)です。分割して作った全ての微小領域内の関数の値のバラツキを一斉に小さくできない(一様連続で無い)関数は、積分可能ではありません。)
(第2の証明)
f(x)が連結な閉区間a≦x≦bで1つながりに連続な関数であれば、閉区間で連続な関数の最大値・最小値の定理によって、f(x)の値はある最大値と最小値の間の値に限られている。
そのように、ある最大値と最小値の間の値に限られている、閉区間で連続な関数f(x)の領域を以下の図の様に2等分する。
(ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。)
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ2を抽出する。
関数f(x)が連続関数の場合は、その差の最大値Δ2は、分割前の領域での関数の最大値と最小値の差Δ1よりも小さくなる。
更に、各領域を2等分する。
(ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。)
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ3を抽出する。
関数f(x)が連続関数の場合は、その差の最大値Δ3は、分割前の領域での差の最大値Δ2よりも小さくなる。
更に、各領域を2等分する操作を繰り返し、
差の最大値Δ4、Δ5、Δ6・・・
を求めて行く。
すると、関数f(x)が連続関数の場合は、領域を分割する毎に、全分割領域での差の最大値Δnは無限に小さくなって行く。
(もし関数の最大値と最小値の差Δnが無限に小さくならない点があったならば、その点は連続では無い点である。連続関数f(x)には、そのような点は無い。)
(一様連続性)
以上の様に、ある関数f(x)の各分割領域を更に2分の1に分割する操作をn回繰り返していき、各分割領域の関数f(x)の最大値と最小値の差(関数の値のばらつき)Δを求める。
(1)そのとき、全ての分割領域での関数の値のばらつきΔの最大値Δnが有限の値で存在すること。
(2)この操作を繰り返して分割領域を無限に小さくすると、
全ての分割領域での関数の値のばらつきの最大値Δnが、無限に小さくなって行く。
(すなわち、全ての分割領域での関数の値のばらつきがΔnより小さく、そのΔnが無限に小さくなっていく)
これが成り立つ関数f(x)の性質を「一様連続」であると言います。
この説明は、以下の様に定義されている一様連続の言い換えです。
「どんなに小さな正の値εについても、全ての分割領域での関数の値のばらつきがε以下にできる、分割領域の小さな幅δ=(b-a)/(2^n)が存在するとき、その関数は一様連続である。」
(一様連続の説明おわり)
その様に無限に小さい関数値のばらつきΔnによる、関数f(x)の値の総和(リーマン積分)への影響は無限に小さい。そのため、この関数f(x)はリーマン積分可能である。
(第2の証明おわり)
これらの証明の様に、「関数f(x)が連結な閉区間a≦x≦bで1つながりに連続な関数であれば、
式S(x)であらわす、リーマン積分で計算する定積分が可能である。」
(微分積分学の基本定理の証明の前半(1)おわり)
(注意)
この被積分関数のf(x)として、異常な関数であるカントール関数も、1つながりに連続な連続関数なので、使えます。
【基本定理の中段の証明】(1)
(1)不定積分S(x)はf(x)の原始関数の1つである。
(原始関数は、連結区間で1つながりの連続関数であり、その全区間内で微分可能な関数です。)
(以上が中段)
(証明開始)
この不定積分S(x)については、
正の値Δが0に近付く極限において、
S(x+Δ)-S(x)=(f(x+Δ/n)+f(x+2Δ/n)+・・・+f(x+nΔ/n))・(Δ/n)
とあらわせるので、
f(x+Δ/n),f(x+2Δ/n)・・・f(x+nΔ/n)の平均値Mは、
M=(f(x+Δ/n)+f(x+2Δ/n)+・・+f(x+nΔ/n))/n=(S(x+Δ)-S(x))/Δ
とあらわせる。
f(x)が少なくとも区間[x,x+Δ]で1つながりに連続な連続関数ならば、
正の値Δが0に近い極限では、f(x)からf(x+nΔ/n)までの値の全てがほとんど同じ値になる。そして、
f(x+Δ/n),f(x+2Δ/n)・・・f(x+nΔ/n)の平均値Mも、
f(x)とほとんど同じ値になる。
Δ→0の極限で、
(S(x+Δ)-S(x))/Δ=M→f(x)
となる。
同様にして、Δ→0の極限で、
(S(x)-S(x-Δ))/Δ=M→f(x)
となる。
これは、 S(x)の左側微分係数と右側微分係数が等しくf(x)になる事を意味する。
よって、S(x)は微分可能であって、その導関数がf(x)になる。
よって、
S(x)はf(x)の原始関数の1つである。
(中段の証明おわり)
【微分積分学の基本定理の後半(2)】
(2)F(x)を、連結区間を定義域とするf(x)の、その連結区間内で1つながりに連続な関数である原始関数の任意の1つとすると、
が成立する。
微分積分学の基本定理の後半(2)が成り立つ事は、以下の様にして証明できる。
(証明開始)
リーマン積分によって、微小領域の要素に分割して集積する積分F(x)の値の、分割数を無限大にする極限の値が計算できる場合は、
すなわち、微小領域の要素を集積する区間を分割して、
その分割した区間毎の要素の集積値の極限値を求める事ができる場合は:
リーマン積分の積分範囲の区間を、2の区間AとBに分割して、
区間Aでの要素の集積値の極限値+区間Bでの要素の集積値の極限値=区間Aと区間Bを合わせた区間での要素の集積値の極限値
になる。
ゆえに、微分積分学の基本定理の証明の後半(2)が成り立つ。
(証明おわり)
「やさしく学べる微分積分」(石村園子)の106ページの形の微分積分学の基本定理を使うと、以下の定理がすぐに導き出せる。
【定理】
連結区間a≦x≦b
の範囲で1つながりに連続な関数f(x)がある場合:
連結区間a<x<b
の範囲で、
f(x)>0
ならば、
連結区間a≦x≦bの範囲で、
f(x)の不定積分F(x)は単調増加である。
(定理の定義おわり)
(証明開始)
関数f(x)が
連結区間a≦x≦b
で連続であるので、
a≦x1<x2≦b
なるx1とx2に関して、
微分積分学の基本定理により、
よって、
F(x)は単調増加である。
(証明おわり)
以下の定理があります。
【定理】
連結区間a≦x≦b
の範囲で連続な関数F(x)がある場合:
連結区間a<x<b
の範囲で、
F’(x)≡f(x)>0
ならば、
a≦x≦bの範囲で、
関数F(x)は単調増加である。
(定理の定義おわり)
平均値の定理を使って、この定理を証明しておきます。
(証明開始)
連結区間a≦x≦b
の範囲で連続な関数F(x)が:
連結区間a<x<b
の範囲で微分可能で、
F’(x)=f(x)
の場合、
平均値の定理によって、
a≦x1<x2≦b
なるx1とx2に関して、
(F(x2)-F(x1))/(x2-x1)=f(x)
となるxが、
a≦x1<x<x2≦b
に、少なくとも1つ存在する。
その範囲で、
f(x)>0
なので、
F(x2)>F(x1)
である。
よって、F(x)は単調増加である。
(証明おわり)
《微分と積分の関係》
なお、全ての種類の関数における、積分前の関数f(x)と、微分前の関数F(x)との、変数xの一部の定義域での微分積分のあり得る関係が以下の図であらわせます。
(なお、F(x)として考えられる関数の、関数が連続な領域内の至るところ微分不可能な関数であるワイエルシュトラス関数等は、連続で無い点を持たないが、微分不可能です。)
(上図で、関数f2(x)は、除去可能な連続で無い点を除去した関数です。関数F(x)は、関数F(x)の連続で無い点を除いた変数xの範囲でf(x)の不定積分であるとともに、f2(x)の不定積分でもあります)
上図の、f(x3)とF(x3)の関数のセットの例:
以下で定義する関数のセットでは、f(x)にx=x3で除去不可能な連続で無い点があって、f(x)は不連続な関数(その点で関数が不連続な関数であって、その点以外の領域では関数が連続な連続関数である)です。
しかし、この連続で無い点を持つ関数f(x)を、その連続で無い点を含む連結区間で定積分することで定義した関数F(x)が、その連続で無い点の位置x3でも変数xで微分可能で、F(x)を微分すると再び連続で無い点を持つf(x)が得られます。
(F(x)の定義)
x≠0の場合:
x=0の場合: F(0)=0,
(導関数f(x))
この関数F(x)はx≠0の場合も、x=0の場合も、微分可能で、
その導関数f(x)は、以下の式であらわせます。
x≠0の場合の微分:
になり、xが0に近づくとー1と1の間を振動します。
この導関数が含むcos(1/x)の関数が以下のグラフであらわす形の関数になるからです。
X=0の場合にも、F(x)は微分可能で:
というように、0になります。
そのため、この導関数f(x)は、x=0で連続ではありませんが、F(x)を微分することで得られます。
この導関数f(x)は積分可能であり、積分するとF(x)になります。
この関数F(x)はx=0で連続な関数です。
この様な複雑な関係の中から、比較的に扱い易い連続関数(連結区間内で関数が1つながりに連続)を使って従来の微分積分学の基本定理が定められています。
また、大学以上の微分積分学では、積分の定義をどんどん拡張して、何でも積分できるようにして、ある関数f(x)を積分して連続で無い点を持つ関数F(x)を得ることができるようにし、その連続で無い点を持つ関数F(x)を微分して関数f(x)を得ることができるように、微分の定義も拡張するというような事も行なわれます。
そのように微分・積分の定義を拡張する入口に、微分積分の基本定理が置かれています。
そのため、微分積分学の基本定理の:
という式の意味することは:
この公式の前提条件以外の条件によってこの式と異なる結果が得られるわけでは無く、
この式を成り立たせるように、f(x)とF(x)を対応させる規則である微分と積分とを矛盾が生じ無い様に定義を修正して、この式を成り立たせているのです。
微分積分学の基本定理の登場により我々に注意が喚起されたメッセージは、
『関数f(x)の積分を計算しようとする場合には、その積分区間における関数の性質(連続である等)を調べなければならない』
というメッセージです。
原始関数を用いて定積分を計算する演算の際に、その定積分の積分区間における関数の性質を調べる事を欠かしてはならない、というメッセージです。
この大切なメッセージについては、日本の高校の積分の授業では、「積分する区間内の全ての変数値に対して関数値が定義されていなければならない」と教えられているようです。先ず、それは必要です。しかし、それだけでは十分ではありません。
そして、高校で習う、
「原始関数F(x)を使って、以下の計算で定積分する。」
に従って計算すると、以下の例の様に、
複合区間を定義域にする高校数学の誤った原始関数F(x)を使った計算では元の関数のグラフの面積が計算できず、
間違った答えになります。
以下の様に、関数f(x)の連続で無い点を定積分の連結区間内に入れてしまうと以下の間違いをおかします。
F(x)=1/xをxで微分したらf(x)=-1/x2になるので、関数f(x)=-1/x2の原始関数がF(x)=1/xであると誤解します。
(原始関数は連結区間で1つながりに連続な関数です)
しかし、積分区間を、f(x)が不連続になる変数値x=0を含めた、xが-1から1までの区間にして、
関数f(x)を定積分しようとして、
複合区間を定義域にする誤った原始関数F(x)を使って、
F(1)-F(-1)=1-(-1)=2
という 計算をすると、明らかに間違えます。
上の図で明らかな様に、-1から1までの範囲でのf(x)の積分の結果は(積分がグラフの面積を表すので)、マイナス無限大にならなければなりません。
しかし、上の計算はそれと全く違う、間違った答えになったのが明らかです。
微分積分学の基本定理によって、
原始関数F(x)を使って被積分関数f(x)の定積分が計算できる事が完全に保証されているのは、f(x)が、その積分区間で連続なときだけです。
それ以外の場合には、その計算の答えが間違っていることがある、という事を認識しなければなりません。
(複合区間を定義域にする誤った原始関数の差で計算するから間違えるのであって、不定積分(必ず連続関数になる)の差で定積分を計算するならば、間違いは起きません。不定積分(いつも連続関数)の差で定積分を求めたと書く答案が一番正しい答案だと思います。)
また、
という計算で得た関数S(x)は不定積分であって、連結区間内で1つながりに連続な関数です。
実際、a>0の場合には、x>0の範囲の定義域だけの関数
S(x)=1/x, (x>0)
だけが得られます。
a≦b<0の場合には、x<0の範囲の定義域だけの関数
S(x)=1/x, (x<0)
だけが得られます。
a=0の場合には、s(x)が計算できません。
このように、
不定積分:
は、
定義域がx<0とx>0との両方の領域を含む関数という複合区間を定義域にする誤った原始関数:
x≠0における
F(x)=1/x, (x≠0)
とは異なります。
(もう1つの注意)
以下の関数f(x)は関数の定義域内の全ての点で連続ですが、1つながりに連続な関数では無いので連続関数ではありません。
高校教科書の誤った連続関数の定義:「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である。」に従うと、これを連続関数とする誤りに陥ります。
《高校数学の「微分積分学の基本定理」の定義》
以下でこの微分積分学の基本定理を考察する。

この切れ切れのノコギリ状の関数f(x)を不定積分した関数S(x)=F(x)を求めてみます。
この関数S(x)=F(x)を微分すると、x=0.5, 1.5, 2.5等では、S(x)=F(x)の微分係数が計算できません。
この関数S(x)=F(x)は原始関数ではありません。
そうなる原因は、被積分関数f(x)が1つながりに連続では無いので連続関数では無かったから、
微分積分学の基本定理の前提条件である、
「関数y=f(x)が、連結区間a≦x≦bの全ての点で連続である」
条件が成り立っていなかったからです。
正しい連続関数の定義に従うと、
「(被積分関数f(x)を連続関数に限定すると)微分と積分が逆演算になる」
と要約した、この微分積分学の基本定理が成り立つ事が言えます。
しかし、高校教科書の誤った連続関数の定義:「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である。」に従うと、
上の事例が、
「(被積分関数f(x)を(正しい定義の)連続関数に限定すると)微分と積分が逆演算になる」
と要約した、この微分積分学の基本定理の反例になっていると誤解しますので、注意する必要があります。
《微分積分学の基本定理の拡張》
なお、微分積分学の基本定理が積分可能性を完全に保証する条件であるf(x)が積分区間で連続でなければならないという条件は、緩める事ができ、
f(x)の不定積分F(x)が積分区間で連続であるだけで良いということが分かっています。
それは、
数学者の藤原松三郎の「微分積分学 第1巻」が、
不連続関数f(x)の積分を広義積分と呼び、
その積分において、関数f(x)の積分区間
a≦x≦b
内で連続な不定積分F(x)が得られたら、
(その積分区間内のxで、f(x)が微分不可能な点があっても良く)
(1)それは、不連続関数f(x)が積分可能である証拠であり、
(2)不定積分F(x)を使った以下の計算で定積分を計算して良い事が書いてあります。
F(b)-F(a)
そのため、定積分が可能な積分区間の判定条件を緩めることができ、
不連続な関数f(x)に対して、
その積分区間で連続な1つながりの不定積分F(x)が見つかったなら、
その不定積分F(x)を使ってその区間の定積分を計算して良いです。
また、小寺平治・著「はじめての微分積分15講」(2,200円)の103ページにも、このことが書いてあります。
(複合区間を定義域にする誤った原始関数の差で計算するから間違えるのであって、不定積分(必ず正しい定義の連続関数になる)の差で定積分を計算するならば、間違いは起きません。不定積分(いつも(正しい定義の)連続関数になる)の差で定積分を求めたと書く答案が一番正しい答案だと思います。)
【ここをクリックした先に、まぼろしの基本定理があります】
リンク:
高校数学の目次
▽基本定理の概要
▽微分積分学の基本定理の定義
▽基本定理の定義のポイント
▽基本定理の対偶
▽微分積分学の基本定理の正しい定義
▽補助定理
▽基本定理の確認
▽基本定理の前半の証明
▽基本定理の中段の証明
▽基本定理の後半の証明
▽微分と積分の関係
▽微分積分学の基本定理の拡張
《基本定理の概要》
【被積分関数の単位】
被積分関数は、均質な基本的な要素の単位で考える。
具体的には、被積分関数を、全て、1つながりに連続する関数を単位にして考える。1つながりに連続する関数は正しく定義された連続関数です。その、1つながりに連続する関数を扱うのであれば、積分の計算で誤りに陥る事を防ぐことができます。
(微分型の)《微分積分学の基本定理》
微分型で表現した微分積分学の基本定理は:
連結区間内で1つながりに連続な関数f(x)がある場合:

が成り立つというものです。
高校の微分積分の教科書では、この定理が当然に成り立つものとして、証明しないで使っています。
(高校の微分積分の参考書に以下の証明があります)
「駿台受験シリーズ 分野別 受験数学の理論7 微分法・積分法の基礎」
https://math.co.jp/contpgm2/w_main.php?oya_id=2&back_id=14#14
(96ページ途中から)



《補足》(この証明での重要ポイント)
以上の証明の中で、関数f(x)がx軸上のxの点において連続関数であるという前提条件を使っている。つまり、関数f(x)が連続関数なので、hを十分小さくすれば、f(x+h)がf(x)に近づく、という前提条件を使った。
この証明の発想の根底に、関数(グラフ)が連続であるという概念が、証明の重要なポイントになっているということに気づくことが大事だ。そこから、連続関数の性質を深く研究する、という数学の研究の焦点が絞られ、その研究の成果が、数学における極限の概念の確立などだろう。
古典的(基礎的)微分積分学を教える高木貞治の「解析概論」では、連続関数を、「ある区域(区間)内において,変数xが連続的に変動するのに伴って連続的に変動する関数f(x) 」と呼んでいる。関数f(x) が連続的に変動するという意味は、関数が区間で、連続的に定義されているという意味である。すなわち、f(x)=1/x という関数のように、x=ー1からx<0までは関数f(x) が定義されていて、x=0では関数が定義されていない。再びx>0からx=1まで関数f(x) が定義されている。といった、関数が区間[-1,1]で連続的には定義されていない関数は連続関数ではないのである。
そういう、数学の根底の思想が、大学の微分積分学によって学ぶことができるハズだった。しかし、最近の大学数学では、微分積分の基礎(微分積分学の根底の思想)は高校で学んできたハズ、として、いきなり、現代数学(位相空間論)の微分積分学から教えるようになっているようです。そういう状況なので、古典的な(基礎的な)微分積分の概念は、自力でしっかり学ぶしかないようです。 ここをクリックした先の「連続関数とは何か」のサイトから、微分積分の基礎の概念を学んでください。
微分積分の高校数学での参考書にも、以上の(駿台の受験シリーズの)参考書のように、数学の発想の礎を作るために良い参考書があった。
一方、高校の微分積分の教科書は偽物で、数学の発想の基礎作りに役立たないと考える。
(補足おわり)

この式が成り立たない場合などあり得ないのではないか?と考える人もいるかもしれません。
この式が成り立たない場合というのは、f(x)が積分出来ない場合です。そもそも積分できなければ、微分する以前に、この式が成り立たないことになります。
また、f(x)が積分して関数F(x)が得られても、関数F(x)が折れ曲がった関数になれば、その折れ曲がり点でF(x)は微分できません。F(x)が微分できなければ、この式が成り立たないことになります。
「関数 f(x) が連結区間内で1つながりに連続している関数f(x)が積分可能である。その積分結果の関数F(x)が、その連結区間で微分可能である。そうして微分した結果は元の関数f(x)に戻る。」というのが(微分型の)微分積分学の基本定理です。
そこには、「関数 f(x) が、ある連結区間内で1つながりに連続している」という条件が付いているのです。
ーー【区間の定義】ーー
「区間」という数学用語は、変数xの数直線上の1つの範囲内の、実数のすき間がない1かたまりの数の集合をあらわす数学用語である。
《神奈川大学》【定義 14.2.4.】
a, b を実数とする. a 以上かつ b 以下の実数をすべて集めた集合を [a, b] と書き, これを閉区 間と呼ぶ.
a より大きくかつ b 未満の実数をすべて集めた集合を (a, b) と書き, これを開区間と呼ぶ.
----定義おわり----
a≦x≦bを満足するxの区間という表現は、a≦x≦bの範囲内の全ての実数xという意味です。
-∞<x<∞という区間もあります。
区間はxの値の範囲を限定するためのa≦x≦bという式とは意味が異なることに注意する必要があります。
「区間」という用語は、特に重要な関数である連続関数の連続性を定義するために必要な、連続関数f(x)の変数xの集合体がいつも持っていなければならない連続性という重要な性質が「区間」という概念を用いてあらわされています。
すなわち、変数xの「区間」の性質で大切なのは、
「区間」のなかに変数xの値が隙間なく存在すること。
つまり所定範囲内での隙間が無い全ての実数の集合という概念が「区間」という用語で定義されています。
例えば:
f(x)=1/xの定義域を(0,∞) (={x|xは0より大きい実数})
とすれば、f(x)は区間で定義された関数です。
g(x)=1/xの定義域を(-∞,0)∪(0,∞)(={x|xは0でない実数})
とすれば、g(x)は区間で定義された関数ではない。
(f(x)とg(x)は定義域が異なっているため、f(x)とg(x)は同じ関数ではない)
(積分型の)《微分積分学の基本定理》
先ず、以下の注意をしておきます。
【注意:間違った計算の例】
以下の図の関数F(x)を考える。

F(x)=C2, (x<0)
F(x)=C1, (x>0)
例えば、C1=1, C2=2, とする。
この関数F(x)を微分して積分してみます。
先ず、微分します。
F'(x)= f(x)=0, (x≠0)
次に、このf(x)を積分します。
ここで、関数f(x)が、変数xが定義される範囲が、連結区間内の全ての実数であること。その連結区間内の全ての実数の変数xで関数f(x)が定義されていなければ、その関数は(変数xの定義域とセットになっているのが関数です)積分してはいけません。
f(x)=0, (x>0) は積分できます。
f(x)=0, (x<0) も積分できます。
しかし、
f(x)=0, (x≠0) は、x≠0 の範囲でx=0の点ではf(x)が定義されていないので、その点をまたいで積分してはいけません。
もし、それを無視して無理に積分すると、
∫F'(x)dx=∫0dx=C, x≠0,
という積分になりますが、
その結果の積分定数Cをどのような値に調整しても、それは、元の関数F(x)には決してなりません。
(「元の関数F(x), (x≠0) は、変数xで関数F(x)が定義されるxの範囲が、x=0が除外されていることで、そのxの範囲(定義域)が、連結区間内の全ての実数では無い関数でした。)
以下で、(積分型の)微分積分学の基本定理を説明します。
(1)関数f(x)を、それが連続する連結区間a≦x≦b
内で定積分(定積分はリーマン積分によって定義されます)することで関数S(x)を求めます。
その関数をxの関数(不定積分)として求めます。
その不定積分は、定積分の計算を実行する苦労をして得た結果を元にして求めます。
(2)一方で、1つながりに連続で、かつ、微分可能な関数F(x)があって、そのF(x)を微分して求めた導関数がf(x)と一致するならば、その関数F(x)がS(x)と一致する。すなわち、S(x)はf(x)の原始関数の1つである。そして、そのF(x)について、
が成立する。というのが微分積分学の基本定理です。
すなわち、そのF(x)が、苦労して求めるべき不定積分S(x)と一致することが分かりました。
そのF(x)を原始関数と名付け、
その原始関数F(x)を使うことにより計算がとても楽になったので 感動した!
という内容が、(積分型の)微分積分学の基本定理です。
-----【原始関数の正しい定義】---------------
(原始関数の正しい定義は、1つながりに連続で、かつ、微分可能な関数F(x)をf(x)の原始関数と定義します)
すなわち、関数F(x)が、連結区間a<x<bのどの点でも連続、かつ、微分可能な関数であれば、F(x)を微分して導関数f(x)が求められる。この場合に、F(x)を関数f(x)の原始関数と言う。
(藤原松三郎の「微分積分学 第1巻」)
すなわち、原始関数は連結区間における連続関数であり1つながりのグラフであると定義されています。
-------原始関数の定義おわり-----------------
(微分可能の定義との関係)あと、微分積分学の基本定理の根底を支えているのが微分可能の定義です。高校数学では、微分可能の定義として、関数が定義される区間の内点(境界点以外の点)が微分可能な場合に右微分係数と左微分係数が一致するとする微分可能の条件しか教えられていません。
変数xの閉区間(a≦x≦b)で定義された関数f(x)の閉区間の境界点=端点でも、片側微分係数があれば、端点でも微分可能です。
大学数学では、変数xが閉区間(a≦x≦b)で定義された関数f(x)の区間の端点x=a,bでも、片側微分係数があるだけで微分可能とする微分可能の定義が詳しく教えられます。そのため、大学数学になって初めて、閉区間で定義された関数f(x)にも微分積分学の基本定理が成り立つことが正しく理解できます。
上図の関数f(x)と、下図の関数F(x)の間では、定義域がx>0での被積分関数のf(x)と不定積分のF(x)との間で微分積分学の基本定理が成り立ちます。ただし、F(x)はx=0の点では微分できないので、x=0を変数xの範囲に含む場合は、F(x)とf(x)の関数の組に微分積分学の基本定理が成り立ちません。
大学数学での定義はそのようなものです。しかし、高校の数学の教科書では、関数f(x)の不定積分S(x)を、f(x)の定積分に基づいて定義しないで、
関数S(x)を微分したらf(x)になった場合、
すなわち、
S’(x)=f(x)
となった場合に、
その原始関数S(x)が不定積分であるとして、
原始関数によって不定積分を定義しています。
そういうふうに定義した「不定積分」
(微分積分学の基本定理が成り立つように不定積分を定義した)
を、微分積分学の基本定理の「不定積分」の定義にすると、
微分積分学の基本定理の意味が不明になります。
教科書の不定積分の定義が微分積分学の基本定理そのものですので、その定義と同じ内容に見える微分積分学の基本定理を説明する意義が有りません。
しかし、「不定積分」がそのように定義されるという高校数学の微分積分の教科書の記述は嘘です。
不定積分は、正しくは、リーマン積分によって定義された定積分を基にして、定義されるのです。
教科書の積分の定義が嘘であるため、微分積分学の基本定理の存在意義があります。
そもそも、積分の概念は、日本の高校の教科書が微分の逆演算で定義しているような狭い貧弱な概念ではありません。積分の概念は、数学の研究対象を微小な部分に分割して研究し、その微小部分を集積した全体にまとめ上げて全体を考えるという、適用範囲が広い概念なのです。
高校数学の微分・積分の教科書は分かりにくいだけで無く、間違いも含まれています。
連続関数の定義は、1817年にBolzanoが中間値の定理を証明する前提条件に定義した連続関数の定義により、歴史上初めて連続関数が正しく定義された(その定義は関数の連続性を区間で定義するものである)。
高校数学の微分積分の教科書で定義する「連続関数」は1817年にBolzanoが定義した連続関数とは異なる定義である。
その偽物の定義に基づくと、微分積分学の基本定理を理解し難くなると考える。
日本の大学数学では、1817年にBolzanoが定義した連続関数を、「区間で連続な関数」と呼んでいる。
関数の連続性に係る定理には、必ず「区間で連続な関数」という言葉が使われる。
高校数学の偽物の「連続関数の定義」は読まない方が良いのではないかと考えます。
(注意1)
ただし、高校数学の数Ⅲの教科書「数学Ⅲ Advanced」(東京書籍)では、1817年にBolzanoが正しく定義した連続関数を、以下のように正しく定義している。
「関数f(x) がある区間Iに属するすべての値xで連続であるとき、f(x) は区間Iで連続である。」
そのように正しい連続関数の定義を教えている高校数学の教科書もあるので、全ての高校数学の教科書がダメというわけでもない。
高校の微分積分を勉強するなら、先ず、大学生向けの微分積分の参考書を読むことを推薦します。高校2年生が勉強するのに適切な、書店で購入できる微分積分の参考書は:
「やさしく学べる微分積分」(石村園子) ¥2000円
が内容がわかり易くて良いと思います。
この本の36ページから45ページまで読めば、微分の概念から始めて合成関数の微分の公式まで学ぶことができます。
高校生は、成人に成長する最終段階にいます。自ら研究して数学の独自分野を開拓する高校生もいると思います。高校生は数学の参考書を高校生向けの本に限定するこだわりは捨て、大学生向けの参考書も、自分に合っていると思えばどんどん吸収していく事が望ましいと考えます。
【微分積分学の基本定理の定義】
関数f(x)が、変数xの実数の連結区間a≦x≦b
において連続な関数である場合を考える。
すなわち、その連結区間で1つながりのグラフであるとする。
(1)
x=aにおいてf(x)が連続であるので、関数の連続の定義に従って、
その連結区間内で関数が連続なので、
x→a でのf(x)の片側極限値と、
x=aにおける値f(a)とが等しい。
(2)
x=bにおいてf(x)が連続であるので、
bについても同様な関係がある。
(3)
また、関数f(x)が定義されている変数xの連結区間で関数f(x)が積分可能である。
そのため、その変数xの連結区間での積分結果の関数F(x)は、その変数xの連結区間で値を持つ。
すなわち、積分結果の不定積分F(x)は被積分関数f(x)と同じ連結区間のxの定義域を持つ。
(4)
連結区間a≦x≦b
の変数xの範囲で定義されている不定積分F(x)を微分する場合に、関数F(x)の境界でも微分可能になり得るように微分の定義が修正されている。
(5)
以上で説明した定義域を持つ関数f(x)に関して、
不定積分F(x)に関して、
連結区間a≦x≦b
の範囲のxに関して以下の関係式が成り立つ。
F’(x)=f(x)
すなわち、不定積分F(x)を微分して得た導関数は、元の連続関数f(x)(その連結区間内で連続な関数f(x))と一致する。
(基本定理の定義:おわり)
《微分積分学の基本定理の定義のポイント》
この基本定理の定義のポイントは、
関数f(x)は、もとの関数が、以下の図の様に大きな定義域の中で積分できない点がある関数であっても、その関数f(x)が、ある連結区間内で1つながりに連続である場合は、関数の定義域をその連結区間内に狭める。
その様に定義域を狭めた連結区間a≦x≦bを新たな定義域にした新たな関数f(x)を考える。
このように、連結区間a≦x≦bとセットにされて定義されている関数f(x)に関わる定理であるというのが第1のポイントです。
その連結区間の外の領域:
x<aや、b<x
の点で、もとの定義域の関数f(x)が、上図の例の様に無限大になっても良い。
元の関数f(x)が無限大になるという異常な領域を除外した連結区間
a≦x≦b
に限って定義された関数f(x)が定理の対象にする関数である。
その様に、区間を限定する事で、この定理を適用できる元の関数f(x)の選択の自由度を高くしているという特徴があります。
その様に関数f(x)が連続である連結区間で、f(x)を不定積分して、下図の関数F(x)が得られます。
(注意)上図の関数f(x)は、x=0で不連続ですが、その連続で無い点以外の図の、関数が連続な連結区間内のxで連続です。その連結区間内で、この関数f(x)が連続関数(その連結区間内で関数が連続)であると定義されます。
下図のF(x)は、連結区間a≦x≦bで定義される。
F(x)をこの連結区間で微分すれば、再び、上図の関数f(x)が得られます。
《下図に各種の関数の集合の包含関係をまとめた》
【問題を解く実用性に優れた形で表現した、微分積分学の基本定理】
大学1年生向けの参考書であるが、高校2年生が勉強するのに良い参考書の、「やさしく学べる微分積分」(石村園子) の106ページに書いてある形の、微分積分学の基本定理が、問題を解く役に立つ、実用性に優れています。
(基本定理の定義の開始)
関数y=f(x)が、
連結区間a≦x≦b
上で連続とする。
(連続関数の定義域は、それが連続な連結区間以上あるということは、いつも意識していて下さい)
関数f(x)を、それが連続する連結区間a≦x≦b
内で定積分(定積分はリーマン積分によって定義されます)することで、以下の関数S(x)を求める。
すると、次のことが成り立つ。
(1)S(x)はf(x)の原始関数の1つの不定積分である。
(原始関数は、連結区間で1つながりの連続関数であり、その全区間内で微分可能な関数です。)
(2)F(x)を、連結区間を定義域とするf(x)の、その連結区間内で1つながりに連続な関数である原始関数の任意の1つとすると、
が成立する。
(定理の定義おわり)
【微分積分学の基本定理の対偶】
この定理の意味を理解するために、この定理の対偶を考えて、対偶によって定理を理解するようにします。
(基本定理の対偶(その1)の定義の開始)
とおいたとき、ある値のcとdで
となるならば、
関数y=f(x)は、
連結区間a≦x≦b のどこかで不連続である。
(対偶(その1)の定義おわり)
この対偶が成り立つだろうかと考えると、f(x)が不連続であっても、S(x)が計算できる(積分可能である)ならば、
とはならず、
この式の左右の辺が等しくなります。
(ここをクリックした先のページを参照)
その場合には、この式の左右の辺が等しく無いという事にはならないので、
そうなる場合にどうなるかという話自体が意味を失います。
このことによって、この定理の対偶(その1)が成立し得ると考えたことが、意味の無い事を考える間違いであり、それでは、この定理を正しく理解していなかったことが分かりました。
再度、この定理を正しく理解したと言える、定理の対偶を考えます。
(基本定理の対偶(その2)の定義の開始)
とおいたとき、ある値のcとdで
という計算をすることができない場合は、
が計算できず、また、関数y=f(x)は、
連結区間a≦x≦b のどこかで不連続である。
(対偶(その2)の定義おわり)
すなわち、この対偶(その2)は、連続で無い点を含む連結区間では積分できないことがあると言う命題です。
この命題は意味を持ちます。
意味のある対偶が考えられたので、対偶の元になった定理も、そのように解釈すべきです。
(基本定理の正しい定義の開始)
関数y=f(x)が、
連結区間a≦x≦b
上で1つながりに連続とする。
その条件が成り立つならば、必ず、
という不定積分S(x)を計算をすることができる。
そして、次のことが成り立つ。
(1)不定積分S(x)はf(x)の原始関数の1つである。
(原始関数は、連結区間で1つながりの連続関数であり、その全区間内で微分可能な関数です。)
(2)F(x)を、連結区間を定義域とするf(x)の、その連結区間内で1つながりに連続な関数である原始関数の任意の1つとすると、
が成立する。
(定理の定義おわり)
すなわち、基本定理の意味は、その定理の命題が、S(x)の式の積分計算を可能にする十分条件(関数f(x)が連結区間で1つながりに連続である)を述べたものであることがわかります。
この基本定理の命題が正しいか否かは、連続関数(その連結区間内で関数が1つながりに連続)が、「関数の積分を可能にする十分条件」になるか否かによって決まる。
(注意)
連結区間で定義された連続な関数f(x)
に対して、
1つの原始関数S(x)が求められた場合に、
その他の全ての原始関数F(x)は、
積分定数Cを用いて、
S(x)+C,
とあらわされる事が、
以下の補助定理を利用して証明できる。
(補助定理)
ある連結区間内の実数全てのxで定義されていて、
その連結区間の全てで微分可能であり、
F'(x)=f(x)
である、原始関数F(x)があるものとする。
被積分関数f(x)が、その連結区間においていつでも0である:
f(x)=0
ならば、
その連結区間で、
F(x)=C
である。
(定理おわり)
(証明)
この補助定理の厳密な証明は、平均値の定理を使って証明します。
しかし、高校生に有りがちな、平均値の定理を証明しないで(証明を知らないで)使うのは関心しません。そういうやり方は他人任せであり、自分では(平均値の定理の証明も含めた)証明の全貌が把握できず、数学センスに反します。
ここでは、平均値の定理の証明を知らない読者のために、
平均値の定理を使わない以下の方法で証明します。
(証明開始)
F’(x)=0なので、
微分の定義から、
(F(x+Δ)- F(x))/Δ=0,
(F(x+2Δ)- F(x+Δ))/Δ=0,
ゆえに、F(x+2Δ)=F(x+Δ)=F(x),
この操作を続けると、
F(x)が微分可能なxの連結区間内では、
F(x)の値は一定値であって、
F(x)=C,
とあらわされる。
(証明おわり)
補足:
上の証明で、
F(x+2Δ)=F(x+Δ)=F(x)
とする操作が続けられるのは、
F(x)が微分可能なxの連結区間内に限られ、
F(x)が微分できない点でこの操作が止まる。
よって、
F(x)=C
とあらわせるxの範囲は、
F(x)が微分可能なxの連結区間内、
すなわち、
f(x)が定義されるxの連結区間内
に限られている。
(注意)
この補助定理のF(x)として、定数では無いカントール関数も、ほとんどの点で微分係数が0なので、使えるのでは無いかと考えるのは誤りです。
なぜならば、カントール関数は、微分不可能な点が無数にあるので、
「その導関数f(x)が連結区間においていつも0である」
という条件が成り立っていないからです。
(補助定理の利用)
この補助定理のF(x)を、
(原始関数F(x)-S(x))
であると考えると、
原始関数F(x)は、
積分定数Cを用いて、
S(x)+C,
とあらわすことができる。
(微分積分学の基本定理の確認その1)
関数f(x)が、以下の図の様に、連結区間内で1つながりに連続な場合は、その連結区間内で関数f(x)が積分可能である。
(定理の確認その2)
一方、以下の図の様に、関数f(x)が1つながりにならず不連続になる連結区間では、関数f(x)の積分が不可能になる場合がある。
そのため、微分積分学の基本定理が成り立っている、ということがわかります。
【基本定理の証明の前半】
この微分積分学の基本定理の証明は、「やさしく学べる微分積分」(石村園子)の106ページの証明を読んで欲しい。
その証明の前半(1)において、
関数y=f(x)が、
連結区間a≦x≦b
上で1つながりに連続とする。
その条件が成り立つならば、必ず、
という計算をすることができる(f(t)が積分可能である) 。
という命題が正しい事は、以下の様にして証明できる。
(第1の証明)
この、「微分積分学の基本定理の要である」積分可能性の証明は、以下では証明の概要のみを説明します。完全な証明は、大学で学ぶ微分積分学から学んでください。完全な証明が行えるためのキーワードは、一様連続性です。
(証明の概要の説明開始)
閉区間で連続な関数は一様連続です(先ず、一様連続性の証明が必要)。すなわち、この関数f(x)をリーマン積分によって、積分区間を均等な微小領域の要素に分割した時に、分割数を多くすると、どの分割部分の微小領域内の関数値のばらつきも、一斉に小さくできる(これを一様連続と言う)。そのため閉区間で連続な関数は、分割数を多くして、一斉に、分割された微小領域内の関数値のバラツキを小さくできるので、積分の値のバラツキを小さくでき、リーマン積分可能です。
すなわち、リーマン積分で分割数を無限大にした極限で、f(x)の値を集積した値が収束する。
よって、f(x)の値を集積した関数S(x)が計算できる。
(第1の証明おわり)
(極限では無限大に発散する点(その点には接続していないが)に向けて連続している(開区間で)連続な関数は、その開区間の領域をいくら細かな微小領域に分割しても、無限大に発散する点の近傍の微小領域内の関数値のバラツキは大きい(バラツキが無限大)です。分割して作った全ての微小領域内の関数の値のバラツキを一斉に小さくできない(一様連続で無い)関数は、積分可能ではありません。)
(第2の証明)
f(x)が連結な閉区間a≦x≦bで1つながりに連続な関数であれば、閉区間で連続な関数の最大値・最小値の定理によって、f(x)の値はある最大値と最小値の間の値に限られている。
そのように、ある最大値と最小値の間の値に限られている、閉区間で連続な関数f(x)の領域を以下の図の様に2等分する。
(ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。)
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ2を抽出する。
関数f(x)が連続関数の場合は、その差の最大値Δ2は、分割前の領域での関数の最大値と最小値の差Δ1よりも小さくなる。
更に、各領域を2等分する。
(ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。)
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ3を抽出する。
関数f(x)が連続関数の場合は、その差の最大値Δ3は、分割前の領域での差の最大値Δ2よりも小さくなる。
更に、各領域を2等分する操作を繰り返し、
差の最大値Δ4、Δ5、Δ6・・・
を求めて行く。
すると、関数f(x)が連続関数の場合は、領域を分割する毎に、全分割領域での差の最大値Δnは無限に小さくなって行く。
(もし関数の最大値と最小値の差Δnが無限に小さくならない点があったならば、その点は連続では無い点である。連続関数f(x)には、そのような点は無い。)
(一様連続性)
以上の様に、ある関数f(x)の各分割領域を更に2分の1に分割する操作をn回繰り返していき、各分割領域の関数f(x)の最大値と最小値の差(関数の値のばらつき)Δを求める。
(1)そのとき、全ての分割領域での関数の値のばらつきΔの最大値Δnが有限の値で存在すること。
(2)この操作を繰り返して分割領域を無限に小さくすると、
全ての分割領域での関数の値のばらつきの最大値Δnが、無限に小さくなって行く。
(すなわち、全ての分割領域での関数の値のばらつきがΔnより小さく、そのΔnが無限に小さくなっていく)
これが成り立つ関数f(x)の性質を「一様連続」であると言います。
この説明は、以下の様に定義されている一様連続の言い換えです。
「どんなに小さな正の値εについても、全ての分割領域での関数の値のばらつきがε以下にできる、分割領域の小さな幅δ=(b-a)/(2^n)が存在するとき、その関数は一様連続である。」
(一様連続の説明おわり)
その様に無限に小さい関数値のばらつきΔnによる、関数f(x)の値の総和(リーマン積分)への影響は無限に小さい。そのため、この関数f(x)はリーマン積分可能である。
(第2の証明おわり)
これらの証明の様に、「関数f(x)が連結な閉区間a≦x≦bで1つながりに連続な関数であれば、
式S(x)であらわす、リーマン積分で計算する定積分が可能である。」
(微分積分学の基本定理の証明の前半(1)おわり)
(注意)
この被積分関数のf(x)として、異常な関数であるカントール関数も、1つながりに連続な連続関数なので、使えます。
【基本定理の中段の証明】(1)
(1)不定積分S(x)はf(x)の原始関数の1つである。
(原始関数は、連結区間で1つながりの連続関数であり、その全区間内で微分可能な関数です。)
(以上が中段)
(証明開始)
この不定積分S(x)については、
正の値Δが0に近付く極限において、
S(x+Δ)-S(x)=(f(x+Δ/n)+f(x+2Δ/n)+・・・+f(x+nΔ/n))・(Δ/n)
とあらわせるので、
f(x+Δ/n),f(x+2Δ/n)・・・f(x+nΔ/n)の平均値Mは、
M=(f(x+Δ/n)+f(x+2Δ/n)+・・+f(x+nΔ/n))/n=(S(x+Δ)-S(x))/Δ
とあらわせる。
f(x)が少なくとも区間[x,x+Δ]で1つながりに連続な連続関数ならば、
正の値Δが0に近い極限では、f(x)からf(x+nΔ/n)までの値の全てがほとんど同じ値になる。そして、
f(x+Δ/n),f(x+2Δ/n)・・・f(x+nΔ/n)の平均値Mも、
f(x)とほとんど同じ値になる。
Δ→0の極限で、
(S(x+Δ)-S(x))/Δ=M→f(x)
となる。
同様にして、Δ→0の極限で、
(S(x)-S(x-Δ))/Δ=M→f(x)
となる。
これは、 S(x)の左側微分係数と右側微分係数が等しくf(x)になる事を意味する。
よって、S(x)は微分可能であって、その導関数がf(x)になる。
よって、
S(x)はf(x)の原始関数の1つである。
(中段の証明おわり)
【微分積分学の基本定理の後半(2)】
(2)F(x)を、連結区間を定義域とするf(x)の、その連結区間内で1つながりに連続な関数である原始関数の任意の1つとすると、
が成立する。
微分積分学の基本定理の後半(2)が成り立つ事は、以下の様にして証明できる。
(証明開始)
リーマン積分によって、微小領域の要素に分割して集積する積分F(x)の値の、分割数を無限大にする極限の値が計算できる場合は、
すなわち、微小領域の要素を集積する区間を分割して、
その分割した区間毎の要素の集積値の極限値を求める事ができる場合は:
リーマン積分の積分範囲の区間を、2の区間AとBに分割して、
区間Aでの要素の集積値の極限値+区間Bでの要素の集積値の極限値=区間Aと区間Bを合わせた区間での要素の集積値の極限値
になる。
ゆえに、微分積分学の基本定理の証明の後半(2)が成り立つ。
(証明おわり)
「やさしく学べる微分積分」(石村園子)の106ページの形の微分積分学の基本定理を使うと、以下の定理がすぐに導き出せる。
【定理】
連結区間a≦x≦b
の範囲で1つながりに連続な関数f(x)がある場合:
連結区間a<x<b
の範囲で、
f(x)>0
ならば、
連結区間a≦x≦bの範囲で、
f(x)の不定積分F(x)は単調増加である。
(定理の定義おわり)
(証明開始)
関数f(x)が
連結区間a≦x≦b
で連続であるので、
a≦x1<x2≦b
なるx1とx2に関して、
微分積分学の基本定理により、
よって、
F(x)は単調増加である。
(証明おわり)
以下の定理があります。
【定理】
連結区間a≦x≦b
の範囲で連続な関数F(x)がある場合:
連結区間a<x<b
の範囲で、
F’(x)≡f(x)>0
ならば、
a≦x≦bの範囲で、
関数F(x)は単調増加である。
(定理の定義おわり)
平均値の定理を使って、この定理を証明しておきます。
(証明開始)
連結区間a≦x≦b
の範囲で連続な関数F(x)が:
連結区間a<x<b
の範囲で微分可能で、
F’(x)=f(x)
の場合、
平均値の定理によって、
a≦x1<x2≦b
なるx1とx2に関して、
(F(x2)-F(x1))/(x2-x1)=f(x)
となるxが、
a≦x1<x<x2≦b
に、少なくとも1つ存在する。
その範囲で、
f(x)>0
なので、
F(x2)>F(x1)
である。
よって、F(x)は単調増加である。
(証明おわり)
《微分と積分の関係》
なお、全ての種類の関数における、積分前の関数f(x)と、微分前の関数F(x)との、変数xの一部の定義域での微分積分のあり得る関係が以下の図であらわせます。
(なお、F(x)として考えられる関数の、関数が連続な領域内の至るところ微分不可能な関数であるワイエルシュトラス関数等は、連続で無い点を持たないが、微分不可能です。)
(上図で、関数f2(x)は、除去可能な連続で無い点を除去した関数です。関数F(x)は、関数F(x)の連続で無い点を除いた変数xの範囲でf(x)の不定積分であるとともに、f2(x)の不定積分でもあります)
上図の、f(x3)とF(x3)の関数のセットの例:
以下で定義する関数のセットでは、f(x)にx=x3で除去不可能な連続で無い点があって、f(x)は不連続な関数(その点で関数が不連続な関数であって、その点以外の領域では関数が連続な連続関数である)です。
しかし、この連続で無い点を持つ関数f(x)を、その連続で無い点を含む連結区間で定積分することで定義した関数F(x)が、その連続で無い点の位置x3でも変数xで微分可能で、F(x)を微分すると再び連続で無い点を持つf(x)が得られます。
(F(x)の定義)
x≠0の場合:
x=0の場合: F(0)=0,
(導関数f(x))
この関数F(x)はx≠0の場合も、x=0の場合も、微分可能で、
その導関数f(x)は、以下の式であらわせます。
x≠0の場合の微分:
になり、xが0に近づくとー1と1の間を振動します。
この導関数が含むcos(1/x)の関数が以下のグラフであらわす形の関数になるからです。
X=0の場合にも、F(x)は微分可能で:
というように、0になります。
そのため、この導関数f(x)は、x=0で連続ではありませんが、F(x)を微分することで得られます。
この導関数f(x)は積分可能であり、積分するとF(x)になります。
この関数F(x)はx=0で連続な関数です。
この様な複雑な関係の中から、比較的に扱い易い連続関数(連結区間内で関数が1つながりに連続)を使って従来の微分積分学の基本定理が定められています。
また、大学以上の微分積分学では、積分の定義をどんどん拡張して、何でも積分できるようにして、ある関数f(x)を積分して連続で無い点を持つ関数F(x)を得ることができるようにし、その連続で無い点を持つ関数F(x)を微分して関数f(x)を得ることができるように、微分の定義も拡張するというような事も行なわれます。
そのように微分・積分の定義を拡張する入口に、微分積分の基本定理が置かれています。
そのため、微分積分学の基本定理の:
という式の意味することは:
この公式の前提条件以外の条件によってこの式と異なる結果が得られるわけでは無く、
この式を成り立たせるように、f(x)とF(x)を対応させる規則である微分と積分とを矛盾が生じ無い様に定義を修正して、この式を成り立たせているのです。
微分積分学の基本定理の登場により我々に注意が喚起されたメッセージは、
『関数f(x)の積分を計算しようとする場合には、その積分区間における関数の性質(連続である等)を調べなければならない』
というメッセージです。
原始関数を用いて定積分を計算する演算の際に、その定積分の積分区間における関数の性質を調べる事を欠かしてはならない、というメッセージです。
この大切なメッセージについては、日本の高校の積分の授業では、「積分する区間内の全ての変数値に対して関数値が定義されていなければならない」と教えられているようです。先ず、それは必要です。しかし、それだけでは十分ではありません。
そして、高校で習う、
「原始関数F(x)を使って、以下の計算で定積分する。」
に従って計算すると、以下の例の様に、
複合区間を定義域にする高校数学の誤った原始関数F(x)を使った計算では元の関数のグラフの面積が計算できず、
間違った答えになります。
以下の様に、関数f(x)の連続で無い点を定積分の連結区間内に入れてしまうと以下の間違いをおかします。
F(x)=1/xをxで微分したらf(x)=-1/x2になるので、関数f(x)=-1/x2の原始関数がF(x)=1/xであると誤解します。
(原始関数は連結区間で1つながりに連続な関数です)
しかし、積分区間を、f(x)が不連続になる変数値x=0を含めた、xが-1から1までの区間にして、
関数f(x)を定積分しようとして、
複合区間を定義域にする誤った原始関数F(x)を使って、
F(1)-F(-1)=1-(-1)=2
という 計算をすると、明らかに間違えます。
上の図で明らかな様に、-1から1までの範囲でのf(x)の積分の結果は(積分がグラフの面積を表すので)、マイナス無限大にならなければなりません。
しかし、上の計算はそれと全く違う、間違った答えになったのが明らかです。
微分積分学の基本定理によって、
原始関数F(x)を使って被積分関数f(x)の定積分が計算できる事が完全に保証されているのは、f(x)が、その積分区間で連続なときだけです。
それ以外の場合には、その計算の答えが間違っていることがある、という事を認識しなければなりません。
(複合区間を定義域にする誤った原始関数の差で計算するから間違えるのであって、不定積分(必ず連続関数になる)の差で定積分を計算するならば、間違いは起きません。不定積分(いつも連続関数)の差で定積分を求めたと書く答案が一番正しい答案だと思います。)
また、
という計算で得た関数S(x)は不定積分であって、連結区間内で1つながりに連続な関数です。
実際、a>0の場合には、x>0の範囲の定義域だけの関数
S(x)=1/x, (x>0)
だけが得られます。
a≦b<0の場合には、x<0の範囲の定義域だけの関数
S(x)=1/x, (x<0)
だけが得られます。
a=0の場合には、s(x)が計算できません。
このように、
不定積分:
は、
定義域がx<0とx>0との両方の領域を含む関数という複合区間を定義域にする誤った原始関数:
x≠0における
F(x)=1/x, (x≠0)
とは異なります。
(もう1つの注意)
以下の関数f(x)は関数の定義域内の全ての点で連続ですが、1つながりに連続な関数では無いので連続関数ではありません。
高校教科書の誤った連続関数の定義:「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である。」に従うと、これを連続関数とする誤りに陥ります。
《高校数学の「微分積分学の基本定理」の定義》
以下でこの微分積分学の基本定理を考察する。

この切れ切れのノコギリ状の関数f(x)を不定積分した関数S(x)=F(x)を求めてみます。
この関数S(x)=F(x)を微分すると、x=0.5, 1.5, 2.5等では、S(x)=F(x)の微分係数が計算できません。
この関数S(x)=F(x)は原始関数ではありません。
そうなる原因は、被積分関数f(x)が1つながりに連続では無いので連続関数では無かったから、
微分積分学の基本定理の前提条件である、
「関数y=f(x)が、連結区間a≦x≦bの全ての点で連続である」
条件が成り立っていなかったからです。
正しい連続関数の定義に従うと、
「(被積分関数f(x)を連続関数に限定すると)微分と積分が逆演算になる」
と要約した、この微分積分学の基本定理が成り立つ事が言えます。
しかし、高校教科書の誤った連続関数の定義:「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である。」に従うと、
上の事例が、
「(被積分関数f(x)を(正しい定義の)連続関数に限定すると)微分と積分が逆演算になる」
と要約した、この微分積分学の基本定理の反例になっていると誤解しますので、注意する必要があります。
《微分積分学の基本定理の拡張》
なお、微分積分学の基本定理が積分可能性を完全に保証する条件であるf(x)が積分区間で連続でなければならないという条件は、緩める事ができ、
f(x)の不定積分F(x)が積分区間で連続であるだけで良いということが分かっています。
それは、
数学者の藤原松三郎の「微分積分学 第1巻」が、
不連続関数f(x)の積分を広義積分と呼び、
その積分において、関数f(x)の積分区間
a≦x≦b
内で連続な不定積分F(x)が得られたら、
(その積分区間内のxで、f(x)が微分不可能な点があっても良く)
(1)それは、不連続関数f(x)が積分可能である証拠であり、
(2)不定積分F(x)を使った以下の計算で定積分を計算して良い事が書いてあります。
F(b)-F(a)
そのため、定積分が可能な積分区間の判定条件を緩めることができ、
不連続な関数f(x)に対して、
その積分区間で連続な1つながりの不定積分F(x)が見つかったなら、
その不定積分F(x)を使ってその区間の定積分を計算して良いです。
また、小寺平治・著「はじめての微分積分15講」(2,200円)の103ページにも、このことが書いてあります。
(複合区間を定義域にする誤った原始関数の差で計算するから間違えるのであって、不定積分(必ず正しい定義の連続関数になる)の差で定積分を計算するならば、間違いは起きません。不定積分(いつも(正しい定義の)連続関数になる)の差で定積分を求めたと書く答案が一番正しい答案だと思います。)
【ここをクリックした先に、まぼろしの基本定理があります】
リンク:
高校数学の目次
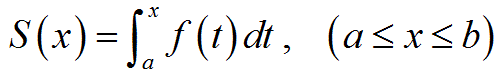
























0 件のコメント:
コメントを投稿