（１８）面の法線への射影を利用した連立方程式の解法

【問】以下の連立方程式を解いて未知数ｓを求めよ。

【解答】
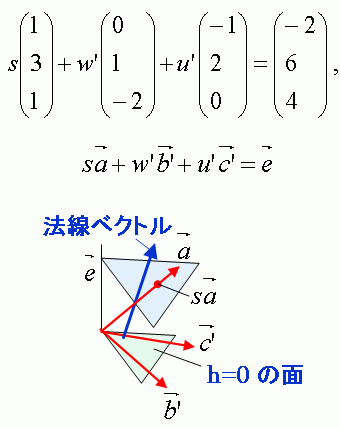
　連立方程式はベクトル方程式とみなして解くとやさしくなります。以下のようにベクトルの張る面に垂直な法線への射影を利用すると連立方程式の１つの未知数ｓを素早く求めることができます。

この式の水平面を張るベクトルｂとｃを、もっと使いやすいベクトルｂ’とｃ’に変更します（同時に未知数ｗとｕも変わります）。
（ここで、水平面には変わりがありません）

このように、成分の１つを０にしたベクトルｂ’とｃ’で水平面を張ります。
このベクトル方程式を以下のようにして解きます。 

（解答おわり）

①　先ず、問題の連立方程式の右辺のベクトルｅのＹ成分のベクトルの高さを６ｚとしました。
②　ベクトルｂとｃの張る面を水平面とする。ベクトルｃのＹ成分の高さは①との関係で、高さ２ｚです。
③　ベクトルｂのＹ成分の高さは①との関係で、高さｚです。
④　ベクトルａのＹ成分の高さは①との関係で、高さ３ｚです。
⑤　ベクトルｃは水平面上のベクトルなので、そのＸ成分はＹ成分による高さ２ｚを打ち消す高さ－２ｚです。
⑥　ベクトルｅのＸ成分の高さは⑤との関係で、高さ－２ｚ・２です。
⑦　ベクトルａのＸ成分の高さは⑤との関係で、高さ２ｚです。
⑧　ベクトルｂは水平面上のベクトルなので、そのＺ成分はＹ成分による高さｚを打ち消す高さ－ｚです。
⑨　ベクトルｅのＺ成分の高さは⑧との関係で、高さ２ｚです。
⑩　ベクトルａのＺ成分の高さは⑧との関係で、高さｚ／２です。

問題の連立方程式のｓに掛かる高さは（⑦＋④＋⑩）であり、右辺の高さは（⑥＋①＋⑨）です。その比を計算してｓが得られました。

【別解】ベクトルの外積を利用して計算すると、以下のように答えが得られます。

（解答おわり）
ベクトルの外積を利用する方が速そうです。


リンク：
高校数学の目次