

計算ミスの減らし方
のサイトがとても参考になります。
そのサイトが推薦している計算の概算方法は、以下のように応用して使います。
・桁数を調節する
・概算でおおよその数値を求めておく
・積極的に約分する
・キリの良いもの、やり易いものから計算する
・計算の省略をしない
・可能な限りスペースを使う
計算ミスの減らし方
<概算でおおよその数値を求めておく>
この手法を発展させた方法の、
図形問題の先行検算手法の使用例を以下に示します。
「図形問題の先行検算方法」
この例も、数ⅠAの【大問3】です。
この問題を解くために、先ず、以下の図を描きます。
図を描いたら、先ずsinBを計算する前に、先行検算として
①: sinBを概算して、
sinB≒1
くらいに、sinBの値の見当をつけます。sinBの計算結果はこの値に近くなければなりません。
そして、sinBを計算して1に近い値を得たので、検算結果は○(良好)です。
(この先行検算をすることにより、図形の長さを2倍や2分の1に間違えるミスを防止できます)
次に、先行検算として、
②: rを概算して、
r≒1-α(1より少し小さい値)くらいに、rの値の見当をつけます。rの計算結果はこの値に近くなければなりません。
rの計算結果は1より少し小さい値に近いので、検算結果は○(良好)です。
次に、先行検算として、
③: IBを概算して、
IB≒√2くらいに値の見当をつけます。計算結果はこの値に近くなければなりません。
IBの計算結果は√2に近いので、検算結果は○(良好)です。
次に、円Oの半径rの値が複雑な数値なので、その値の長さを図に書き込むと図がきたなくなり計算の見通しが悪くなりますので、 計算の見通しを良くするため、パラメータrを単位にして図形の長さをあらわすように、もう1つの図(以下の図)を描きます。
④: 外接円Oの半径Rを概算して、
R≒1/3くらいに値の見当をつけます。計算結果はこの値に近くなければなりません。
Rの計算結果は1/3に近いので、検算結果は○(良好)です。
ここで、円Oと円Iの関係を調べるために新たに以下の図を描きます。
次に、新たに以下の図を描いて問題を解きます。
次に、更に以下の図を描いて問題を解きます。
⑤: GM/CGを概算して、
GM/CG≒1/2程度の値に見当をつけます。計算結果はこの値に近くなければなりません。
この問題はスーパーメネラウスの定理を適用して上図のように解きます。
GM/CG=1/2になりましたので、検算結果は○(良好)です。
(解答おわり)
(補足) ここで、上の図では、Gが三角形FBCの重心になっているので、辺FBに対する重心Gの高さと頂点Cの高さの比から答えが出せます。それが正解です。しかし、重心以外の点についても、スーパーメネラウスの定理を適用することで問題を解くことができます。
リンク:
高校数学の目次
のサイトがとても参考になります。
そのサイトが推薦している計算の概算方法は、以下のように応用して使います。
計算ミスを減らしたい
<計算の仕方を見直す方法>・桁数を調節する
・概算でおおよその数値を求めておく
・積極的に約分する
・キリの良いもの、やり易いものから計算する
・計算の省略をしない
・可能な限りスペースを使う
計算ミスの減らし方
<概算でおおよその数値を求めておく>
この手法を発展させた方法の、
図形問題の先行検算手法の使用例を以下に示します。
「図形問題の先行検算方法」
この例も、数ⅠAの【大問3】です。
この問題を解くために、先ず、以下の図を描きます。
図を描いたら、先ずsinBを計算する前に、先行検算として
①: sinBを概算して、
sinB≒1
くらいに、sinBの値の見当をつけます。sinBの計算結果はこの値に近くなければなりません。
そして、sinBを計算して1に近い値を得たので、検算結果は○(良好)です。
(この先行検算をすることにより、図形の長さを2倍や2分の1に間違えるミスを防止できます)
次に、先行検算として、
②: rを概算して、
r≒1-α(1より少し小さい値)くらいに、rの値の見当をつけます。rの計算結果はこの値に近くなければなりません。
次に、先行検算として、
③: IBを概算して、
IB≒√2くらいに値の見当をつけます。計算結果はこの値に近くなければなりません。
次に、円Oの半径rの値が複雑な数値なので、その値の長さを図に書き込むと図がきたなくなり計算の見通しが悪くなりますので、 計算の見通しを良くするため、パラメータrを単位にして図形の長さをあらわすように、もう1つの図(以下の図)を描きます。
④: 外接円Oの半径Rを概算して、
R≒1/3くらいに値の見当をつけます。計算結果はこの値に近くなければなりません。
Rの計算結果は1/3に近いので、検算結果は○(良好)です。
ここで、円Oと円Iの関係を調べるために新たに以下の図を描きます。
次に、新たに以下の図を描いて問題を解きます。
次に、更に以下の図を描いて問題を解きます。
⑤: GM/CGを概算して、
GM/CG≒1/2程度の値に見当をつけます。計算結果はこの値に近くなければなりません。
この問題はスーパーメネラウスの定理を適用して上図のように解きます。
GM/CG=1/2になりましたので、検算結果は○(良好)です。
(解答おわり)
(補足) ここで、上の図では、Gが三角形FBCの重心になっているので、辺FBに対する重心Gの高さと頂点Cの高さの比から答えが出せます。それが正解です。しかし、重心以外の点についても、スーパーメネラウスの定理を適用することで問題を解くことができます。
リンク:
高校数学の目次


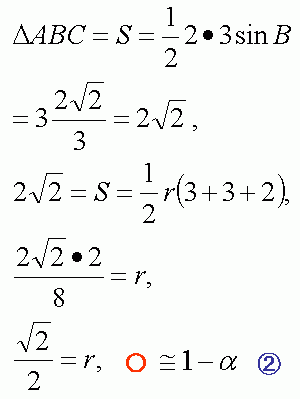











0 件のコメント:
コメントを投稿