

高校2年の微分の授業で、対数微分を教えていない。
そもそも、対数関数の微分を高校3年になってから数Ⅲでようやく教えている。
しかし、対数微分を教えないと微分の重要な公式を導き出す(証明する)こともできない。証明していない公式を覚えさせて使わせるという、数学教育の崩壊に近いことも行われているようです。
そういう不健全状態を改善するために、高校2年生も、以下に説明する対数微分を覚えるべきと考えます。
【対数微分法】
「微分積分学入門」(横田 壽)77ページ
両辺の対数をとって微分する方法を対数微分法(logarithmic differentiation) といいます.
y = xn のn が整数のときの導関数は,例題2.4 で求めました.
しかし, y = xα のα が実数 のときの導関数は例題2.4 で用いた方法では求められません(なぜでしょう?).
しかしもう大丈 夫です.なぜなら私たちには対数微分法があるからです.
以下で、対数微分法の例を説明します。
【問題】
以下の式1は、(値が負になっても良い)実数αを使って表されている。ここで、
x>0,
である。 この式1を微分せよ。
【解答】
式1の両辺の対数をとる。
この式2の両辺を微分する。
(対数関数の微分の公式を使う)
こうして、求める微分の式5が得られました。
(解答おわり)
この解答から、以下の、 xの実数乗の式の微分の公式が得られました。
ただし、x>0,であり、
αは、値が負でも良い実数である。
リンク:
高校数学の目次
そもそも、対数関数の微分を高校3年になってから数Ⅲでようやく教えている。
しかし、対数微分を教えないと微分の重要な公式を導き出す(証明する)こともできない。証明していない公式を覚えさせて使わせるという、数学教育の崩壊に近いことも行われているようです。
そういう不健全状態を改善するために、高校2年生も、以下に説明する対数微分を覚えるべきと考えます。
【対数微分法】
「微分積分学入門」(横田 壽)77ページ
両辺の対数をとって微分する方法を対数微分法(logarithmic differentiation) といいます.
y = xn のn が整数のときの導関数は,例題2.4 で求めました.
しかし, y = xα のα が実数 のときの導関数は例題2.4 で用いた方法では求められません(なぜでしょう?).
しかしもう大丈 夫です.なぜなら私たちには対数微分法があるからです.
以下で、対数微分法の例を説明します。
【問題】
以下の式1は、(値が負になっても良い)実数αを使って表されている。ここで、
x>0,
である。 この式1を微分せよ。
【解答】
式1の両辺の対数をとる。
この式2の両辺を微分する。
(対数関数の微分の公式を使う)
(解答おわり)
この解答から、以下の、 xの実数乗の式の微分の公式が得られました。
ただし、x>0,であり、
αは、値が負でも良い実数である。
リンク:
高校数学の目次



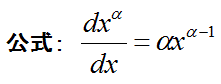
0 件のコメント:
コメントを投稿