【問1】(難問)
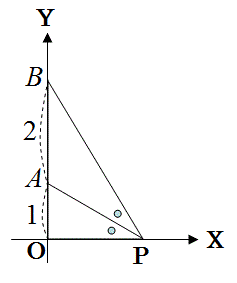
上の図のように、OA=1,OB=3とする。
∠OPA=∠APB
のとき、
OPの長さを求めなさい。
【解答】
この問題では、以下の様に、水平線上の点の高さの比の公式を使って解く。
先ず、線分PAを、高さ0(0h)の水平線であるものとする。
点Bの水平線上の高さを(2h)とすると、
点Oの高さは(-h)になる。
∠OPA=∠APBであり
水平線PAに対する傾きが同じ斜め線に、この高さの比が反映されて、
BP:OP=2:1
になる。
ここで、正三角形を2分した直角三角形の各辺同士の長さの比を思い出すこと。
直角三角形OPBは、斜辺と他の辺の比が、正三角形を2分した直角三角形の斜辺と他の辺の比と同じなので、
その直角三角形と相似である。
よって、
∠OPB=60°
正三角形を2分した直角三角形との相似比を用いて計算した結果、
OP=√3
である。
(解答おわり)
(補足)
この計算過程を答案に書く場合に、
(もし覚えていれば)
「三角形の角の二等分線の公式により、
OP:BP=OA:BA=1:2
である。」
と、答案に書いても良いが、
上に書いた様に考えて解く方が、
より応用が利く解き方なので、
優れていると思う。
リンク:
中学数学の目次
上の図のように、OA=1,OB=3とする。
∠OPA=∠APB
のとき、
OPの長さを求めなさい。
【解答】
この問題では、以下の様に、水平線上の点の高さの比の公式を使って解く。
先ず、線分PAを、高さ0(0h)の水平線であるものとする。
点Bの水平線上の高さを(2h)とすると、
点Oの高さは(-h)になる。
∠OPA=∠APBであり
水平線PAに対する傾きが同じ斜め線に、この高さの比が反映されて、
BP:OP=2:1
になる。
ここで、正三角形を2分した直角三角形の各辺同士の長さの比を思い出すこと。
直角三角形OPBは、斜辺と他の辺の比が、正三角形を2分した直角三角形の斜辺と他の辺の比と同じなので、
その直角三角形と相似である。
よって、
∠OPB=60°
正三角形を2分した直角三角形との相似比を用いて計算した結果、
OP=√3
である。
(解答おわり)
(補足)
この計算過程を答案に書く場合に、
(もし覚えていれば)
「三角形の角の二等分線の公式により、
OP:BP=OA:BA=1:2
である。」
と、答案に書いても良いが、
上に書いた様に考えて解く方が、
より応用が利く解き方なので、
優れていると思う。
リンク:
中学数学の目次



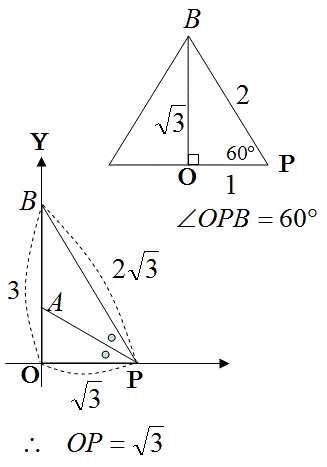
0 件のコメント:
コメントを投稿