円に内接する四角形の対角線の交差点までの長さの計算は、
2つの場合に応じて、解き方が変わります。
【第1の場合】
三角形AEDと三角形BECは相似です。
△AED ∽ △BEC
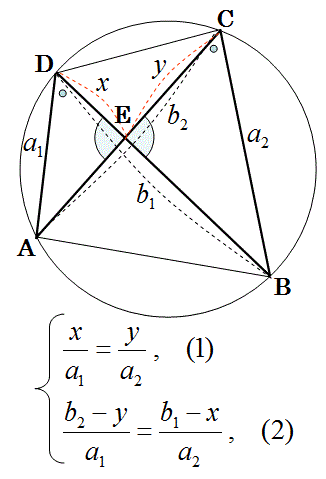
上図のように、三角形AEDの辺ADの長さa1と三角形BECの辺BCの長さa2が異なる場合は、
相似な三角形同士で辺の比が同じであることを表す方程式1と2を立てて、以下のように計算して長さxとyを求めます。
【第2の場合】
上図のように、三角形AEDの辺ADと三角形BECの辺BCの長さaが同じ場合は、
先ず、頂点Dの足Fを考え、FB=C2を計算する。
この式は、ここをクリックした先に書きました。
そして、このC2を使った式6の計算で長さzを求めます。
この式6は、以下の計算で導き出します。
この式を変形して式6を得る。
(補足)
この第2の場合で、線分DCの長さもわかっている場合は、
(1)
C2=(AB+DC)/2
で計算できます。
また、
(2)相似な△ECDと△EBAの辺CDの長さと辺BAの長さが等しくない場合は、第1の場合の計算を使うことができます。
(3)辺CDの長さと辺BAの長さが等しく、辺ADの長さと辺BCの長さも等しい場合は、四角形ABCDが長方形になり、簡単に解けます。
リンク:
中学数学の目次
2つの場合に応じて、解き方が変わります。
【第1の場合】
三角形AEDと三角形BECは相似です。
△AED ∽ △BEC
上図のように、三角形AEDの辺ADの長さa1と三角形BECの辺BCの長さa2が異なる場合は、
相似な三角形同士で辺の比が同じであることを表す方程式1と2を立てて、以下のように計算して長さxとyを求めます。
【第2の場合】
上図のように、三角形AEDの辺ADと三角形BECの辺BCの長さaが同じ場合は、
先ず、頂点Dの足Fを考え、FB=C2を計算する。
この式は、ここをクリックした先に書きました。
そして、このC2を使った式6の計算で長さzを求めます。
この式6は、以下の計算で導き出します。
この式を変形して式6を得る。
(補足)
この第2の場合で、線分DCの長さもわかっている場合は、
(1)
C2=(AB+DC)/2
で計算できます。
また、
(2)相似な△ECDと△EBAの辺CDの長さと辺BAの長さが等しくない場合は、第1の場合の計算を使うことができます。
(3)辺CDの長さと辺BAの長さが等しく、辺ADの長さと辺BCの長さも等しい場合は、四角形ABCDが長方形になり、簡単に解けます。
リンク:
中学数学の目次





0 件のコメント:
コメントを投稿