【問１】（ややこしい問題）
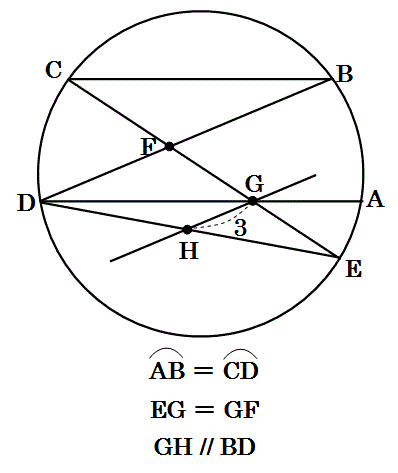
上図のように、１辺の長さが５の正方形を底面とし、高さが１０の直方体ＡＢＣＤ－ＥＦＧＨがある。点ＰをＢＰ＝３となるように辺ＢＦ上に、点ＱをＤＱ＝５となるように辺ＤＨ上にそれぞれとる。３点Ａ，Ｐ，Ｑを通る平面と辺ＣＧとの交点をＲとする。このとき、頂点Ｃから面ＡＰＲＱにひいた垂線の長さを求めよ。
（注意）
この問題は、良く整理して解かないと、計算の森に迷い込むややこしい問題です。以下の理由により、安易に解答を見ないよう注意してください。このややこしい問題を自力で解いてから解答を見てください。
（解けるまで解答を見ない理由）
出題高校の意図を推測すると、「単にいろいろな難問の解き方を覚えて知っている学生よりも、想像力豊かで知能が高く融通性に富んだ学生の方を合格させたい」
という意図がある考えます。
そのため、このややこしい問題を学ぶ目的は、
この問題を簡単に解こうとする努力により知能を高めるホルモンが分泌されて知能を高めること、
を第１の目的にするのが良いと考えます。
そのため、この問題を自力で解くまでは解答を見ずに、ベストな勉強方法としては、問題を解く努力をした後（解けないで寝て良い）寝ている間に知能ホルモンの分泌をさせる。それを何回か繰り返すのが良いと考えます。
（解答の方針）
（１）難問が解けずに寝るとき、寝ている間も何とか問題を解こうとして、そのために、問題を考え易い簡単な形にして、解こうとするだろうと思います。
そのように簡単な形に問題を変換して考えることが、あらゆる難問を解くコツです。
（２）立体図形は、平面図形の問題に変換して解く。
（３）第１の面への垂線を求める問題は、第１の面上の１本の直線に垂直な第２の面を考える。その第２の面上の直線で、第１の面に垂直な直線が求める垂線である。
この問題の解答は、ここをクリックした先のページにあります。
リンク：
中学数学の目次
【問題１】（難問）
上図の線分の間に、
ＡＲ：ＲＢ＝１：３と
ＡＱ：ＱＣ＝２：１
の線分の長さの比の関係があるとき、
（１）ＢＰ：ＰＣを求めよ。
（２）ＡＯ：ＯＰを求めよ。
（重要な注意）
以下で、このページに問題の解き方、解答を書きます。
その理由は、この種の問題を解くために推薦する解答方法を教えたいためです。
この難問を、自力で解く努力をして知能ホルモンを分泌させたい人は、以下を読まないで、この問題を自力で解く努力をしてください。
それ以外の方には、この難問を解く方法で、自力では考え出すことが難しいと思われる究極の方法の使い方を説明するので、その方法を学んでください。
【解答はじめ】
以下の図のように、水平線の位置を仮定して、その水平線上の点の高さの比を考えます。その高さの比を線分の長さの比に反映させて解くのが「究極の方法」です。
上図のように水平線の位置を定めて点の高さの比をカッコ()の中に書いて行きます。
その高さの比から線分の長さの比を考えると、
ＲＯ：ＯＣ＝３：２
であることがわかります。
次に、視点を変えて、水平線を以下の図のように定めて点の高さの比を考えます。
上図のように水平線の位置を定めて点の高さの比を考えると、
ＰＯ：ＯＡ＝３：７
ＢＯ：ＯＱ＝９：１
であることがわかります。
次に、再度、視点を変えて、水平線を以下の図のように定めて点の高さの比を考えます。
上図のように水平線の位置を定めて点の高さの比を考えると、
ＢＰ：ＰＣ＝６：１
であることがわかります。
以上で、
（１） ＢＰ：ＰＣ＝６：１
（２） ＡＯ：ＯＰ＝７：３
が全て求められました。
（解答おわり）
リンク：
中学数学の目次
【問１】（難問）
上図のように、円周上に５点Ａ，Ｂ，Ｃ，Ｄ，Ｅがあり、弧ＡＢ＝弧ＣＤである。
また、線分ＣＥと線分ＢＤの交点をＦ、線分ＣＥと線分ＡＤの交点をＧとし、線分ＤＥ上にＢＤ//ＧＨとなる点Ｈをとる。
ＥＧ＝ＧＦ，ＧＨ＝３のとき、線分ＥＧの長さを求めなさい。
（注意）
この問題は難問です。以下の理由により、安易に解答を見ないよう注意してください。この難問を自力で解いてから解答を見てください。
（解けるまで解答を見ない理由）
出題高校の意図を推測すると、「単にいろいろな難問の解き方を覚えて知っている学生よりも、想像力豊かで知能が高く融通性に富んだ学生の方を合格させたい」
という意図がある考えます。
そのため、この難問を学ぶ目的は、
この難問を解こうとする努力により知能を高めるホルモンが分泌されて知能を高めること、
を第１の目的にするのが良いと考えます。
そのため、この難問を自力で解くまでは解答を見ずに、ベストな勉強方法としては、難問を解く努力をした後（解けないで寝て良い）寝ている間に知能ホルモンの分泌をさせる。それを何回か繰り返すのが良いと考えます。
（難問の解き方）
（１）難問が解けずに寝るとき、寝ている間も何とか問題を解こうとして、そのために、問題を考え易い簡単な形にして、解こうとするだろうと思います。
そのように簡単な形に問題を変換して考えることが、あらゆる難問を解くコツです。
（２）図形の難問は、図形を完成させてから解く。
（３）相似図形があったら、その相似図形の辺の関係式を全て書いて、その式を自分で見て考えられるようにする。
この問題の解答は、ここをクリックした先にあります。
リンク：
中学数学の目次
【問１】（難問）
上図のように、円Ｏと円Ｏの周上にない２点Ａ，Ｂがある。
円Ｏの直径ＰＱをひいたとき、ＡＰ＝ＢＱとなる直径ＰＱを１つ、定規とコンパスを用いて作図し、点Ｐおよび点Ｑの位置を示す文字Ｐ，Ｑも書きなさい。
ただし、作図に用いた線は消さないでおくこと。
（注意）
この問題は難問です。以下の理由により、安易に解答を見ないよう注意してください。この難問を自力で解いてから解答を見てください。
（解けるまで解答を見ない理由）
出題高校の意図を推測すると、「単にいろいろな難問の解き方を覚えて知っている学生よりも、想像力豊かで知能が高く融通性に富んだ学生の方を合格させたい」
という意図があると考えます。
そのため、この難問を学ぶ目的は、
この難問を解こうとする努力により知能を高めるホルモンが分泌されて知能を高めること、
を第１の目的にするのが良いと考えます。
そのため、この難問を自力で解くまでは解答を見ずに、ベストな勉強方法としては、難問を解く努力をした後（解けないで寝て良い）寝ている間に知能ホルモンの分泌をさせる。それを何回か繰り返すのが良いと考えます。
（難問の解き方）
難問が解けずに寝るとき、寝ている間も何とか問題を解こうとして、そのために、問題を考え易い簡単な形にして、解こうとするだろうと思います。
そのように簡単な形に問題を変換して考えることが、あらゆる難問を解くコツです。
この問題の解答は、ここをクリックした先にあります。
リンク：
中学数学の目次
新型コロナウイルス感染対策
【円の中の点に拡張した円周角の定理】
上図のように、円の中の点Ａにかかわる円周角の定理が成り立ちます。
この式を自力で証明して
よく覚えてください。
リンク：
中学数学の目次
【円の外の点に拡張した円周角の定理】
上図のように、円の外の点Ａにかかわる円周角の定理が成り立ちます。
この式を自力で証明して
よく覚えてください。
リンク：
中学数学の目次
上図のように、１辺の長さが５の正方形を底面とし、高さが１０の直方体ＡＢＣＤ－ＥＦＧＨがある。点ＰをＢＰ＝３となるように辺ＢＦ上に、点ＱをＤＱ＝５となるように辺ＤＨ上にそれぞれとる。３点Ａ，Ｐ，Ｑを通る平面と辺ＣＧとの交点をＲとする。このとき、頂点Ｃから面ＡＰＲＱにひいた垂線の長さを求めよ。
