
佐藤の数学教科書「図形と方程式」編の勉強
【問1】
座標原点を中心にする半径1の円(x2+y2=1)と直線ax+by=1との交点の座標を求めよ。
(予備知識)
受験問題のときは、円と直線の方程式の問題は、図形の方程式をベクトルの式であらわして、図形で考えます。方程式を解いて計算するのは、計算の見通しがあまり良くありません。それに対して、ベクトルを利用した図形の問題を考えることは、計算の見通しを良くするからです。
円の式は、x2+y2=1 (式1)
直線の式は、ax+by=1 (式2)
式1と式2を連立して交点B(x,y)とCの座標を求める。
(ベクトルを利用した計算技術を使う)
式2は、下の図のベクトルBとベクトルAの内積です。

上図のように、ベクトルA(a,b)に平行な単位ベクトルH(a,b)/f を考える。
単位ベクトルH
である。
式2をベクトルBと単位ベクトルHとの内積の式に書き直す。
単位ベクトルHに垂直な単位ベクトル
を考える。
ベクトルBをベクトルHとベクトルJの合成であらわす。
式1と式2を連立するのみでベクトルBの方向を定める場合は、ベクトルBの方向は、単位ベクトルJとベクトルBの内積が以下の式6のように負になる方向に向いている場合もありえる。
式4のx成分とy成分は以下の式になる。
よって、接点BとCの座標(x,y)は、以下の式であらわせる。
(点Bの座標)
sとtには、式3と式5を代入する。
(点Cの座標)
sとtには、式3と式6を代入する。
(解答おわり)
リンク:
高校数学の目次
(5)複素数平面での円と直線の交点
【問1】
座標原点を中心にする半径1の円(x2+y2=1)と直線ax+by=1との交点の座標を求めよ。
(予備知識)
受験問題のときは、円と直線の方程式の問題は、図形の方程式をベクトルの式であらわして、図形で考えます。方程式を解いて計算するのは、計算の見通しがあまり良くありません。それに対して、ベクトルを利用した図形の問題を考えることは、計算の見通しを良くするからです。
円の式は、x2+y2=1 (式1)
直線の式は、ax+by=1 (式2)
式1と式2を連立して交点B(x,y)とCの座標を求める。
(ベクトルを利用した計算技術を使う)
式2は、下の図のベクトルBとベクトルAの内積です。

上図のように、ベクトルA(a,b)に平行な単位ベクトルH(a,b)/f を考える。
単位ベクトルH
である。
式2をベクトルBと単位ベクトルHとの内積の式に書き直す。
単位ベクトルHに垂直な単位ベクトル
を考える。
ベクトルBをベクトルHとベクトルJの合成であらわす。
式1と式2を連立するのみでベクトルBの方向を定める場合は、ベクトルBの方向は、単位ベクトルJとベクトルBの内積が以下の式6のように負になる方向に向いている場合もありえる。
式4のx成分とy成分は以下の式になる。
(点Bの座標)
sとtには、式3と式5を代入する。
sとtには、式3と式6を代入する。
リンク:
高校数学の目次
(5)複素数平面での円と直線の交点

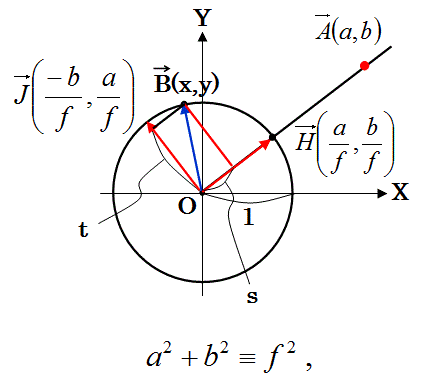








0 件のコメント:
コメントを投稿