

佐藤の数学教科書「ベクトル」編の勉強
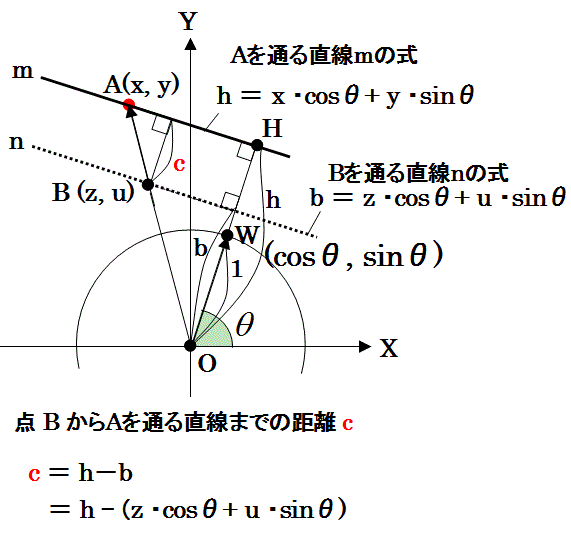
先に、上図のように、原点と直線の間の距離がhである直線の式(点Aを通る直線mの式)が得られました。
【問】
点Aを通る直線mと、空間上の任意の位置の点B(z,u)との間の距離cを求める公式を導け。
この問題を解く手順は、下図のように、点Bを通り、直線mに平行な直線nを考えます。その直線の原点からの距離をbとすると、その直線nの式は下図の式になります。
その結果、上図のように、点Aを通る直線mと、空間上の任意の位置の点B(z,u)との間の距離cは、平行な直線mと直線nとの間の距離h-bになります。
よって、上の式がh-bを与える公式です。
この点Bと直線の距離の公式は、数Ⅱの「図形と方程式」で学ぶ予定です。
この公式を上図のようにしてベクトルの内積で素早く導出することをおぼえておけば、よりやさしく公式を覚えられると思います。
リンク:
高校数学の目次
先に、上図のように、原点と直線の間の距離がhである直線の式(点Aを通る直線mの式)が得られました。
【問】
点Aを通る直線mと、空間上の任意の位置の点B(z,u)との間の距離cを求める公式を導け。
この問題を解く手順は、下図のように、点Bを通り、直線mに平行な直線nを考えます。その直線の原点からの距離をbとすると、その直線nの式は下図の式になります。
その結果、上図のように、点Aを通る直線mと、空間上の任意の位置の点B(z,u)との間の距離cは、平行な直線mと直線nとの間の距離h-bになります。
よって、上の式がh-bを与える公式です。
この点Bと直線の距離の公式は、数Ⅱの「図形と方程式」で学ぶ予定です。
この公式を上図のようにしてベクトルの内積で素早く導出することをおぼえておけば、よりやさしく公式を覚えられると思います。
リンク:
高校数学の目次

0 件のコメント:
コメントを投稿