

大学への数学「ベクトル」編の勉強
(注意)この問題の解き方はややこしいものですが、複素数平面を使うと(ここをクリック)計算が大分楽になります。
(注意)以下の問1では三角関数を使った解き方を書きます。
問2では、三角関数を使わないでベクトルの内積だけを使って比較的楽に解きます。
【問1】下図のように円周上に3点ABCがある。この場合に、∠BAC=βの余弦=cosβをベクトルの内積を利用して計算して、円周角の定理を再確認せよ。
【解答(その1)】
上図のベクトルa、b、cを以下の式(1)(2)(3)であらわす。
cosβは以下の式で計算できる。
この式の各項を以下で計算する。
cosβは以下の式になる。
この答えを場合分けすると以下の式になる。
また、点Aが点B又はC上にある場合は値が不定になる。
(解答おわり)
この式は、円周角の余弦=cosβは、点Aが円周上の点Bか点Cの位置を横切ると、値の正負が逆になることをあらわしている。
つまり、点Aの位置が円周上の第1の円弧の上にあると値がプラスで、それ以外の領域にあると、値がマイナスになる。また、点Aが点B又はC上にある場合は値が不定になる。
このように、cosβは、点Aの位置によって値が変わるので、cosβの値は、一定の値になるというわけではない。
【解答(その2)】
角度βが一定であることは、以下の計算でも確認できる。
式a2からa4によって、ベクトルavとbvとcvを、ベクトルaとbとcを反時計回りに90°回転したベクトルであると定義する。
ただし、この角度βは、点Aが線分BCの右側にある場合の角度であり、点Aが線分BCの左側に来ると、角度の符号が逆になる。
ひし形の対角線の直交の公式により、式a8が成り立つ。
式a7は、ベクトルavとcvがベクトルaとcに直交するベクトルであるので成り立つ。
式a11によって、tanβの値は、点Aの位置が線分BCの右側にある限り、点Aの位置によらず一定の値になる。
(解答おわり)
【問2】下図のように円周上に3点ABCがある。この場合に、以下の式1の関係が成り立つことを示せ。
ただし、この図における各ベクトルの間には以下の関係が成り立っている。
(注意事項)ベクトルの各成分はベクトル名に添え字をつけて、a1というふうにあらわすこと。そうすれば、a12+a22=1という関係が成り立つa1とa2の関係が計算の際に難なく思い出して使うことができるようになるからです。
【解答の方針】
(1)この問題が出たら、これは円周角の問題だと気付くことがベスト。
各ベクトルの内積と円周角との関係を示して、円周角の定理が式(1)であらわされることを示すのが一番速い解答になります。
(2)円周角の問題であると気付かなかった場合は、この問題を(問1)のように、三角関数で解くのが2番目に速く解けます。
(3)以上の2つの視点に気付かなかった場合は、以下のように地道にベクトルの計算をします。
ベクトルの計算にあたって、この問題のように難しい問題の場合は、ベクトルを互いに直交する2方向の成分に分解して成分の計算を行います。そうすれば、以下のように計算を進めることができ、問題が解けるようになります。
【解答】
式(1)の左辺を、べクトルを成分に分解して計算する。
次に、式(1)の右辺の各項を計算する。
この式(3)と(4)の結果を合わせて、式(1)の右辺を計算する。
この式(5)は、式(1)の左辺を計算した式(2)と等しい。
よって式(1)が成り立つ。
(解答おわり)
リンク:
ベクトルの角度を複素数平面で計算できることを初めて知ったら試してみよう
高校数学の目次
(注意)この問題の解き方はややこしいものですが、複素数平面を使うと(ここをクリック)計算が大分楽になります。
(注意)以下の問1では三角関数を使った解き方を書きます。
問2では、三角関数を使わないでベクトルの内積だけを使って比較的楽に解きます。
【問1】下図のように円周上に3点ABCがある。この場合に、∠BAC=βの余弦=cosβをベクトルの内積を利用して計算して、円周角の定理を再確認せよ。
【解答(その1)】
上図のベクトルa、b、cを以下の式(1)(2)(3)であらわす。
cosβは以下の式になる。
(解答おわり)
この式は、円周角の余弦=cosβは、点Aが円周上の点Bか点Cの位置を横切ると、値の正負が逆になることをあらわしている。
つまり、点Aの位置が円周上の第1の円弧の上にあると値がプラスで、それ以外の領域にあると、値がマイナスになる。また、点Aが点B又はC上にある場合は値が不定になる。
このように、cosβは、点Aの位置によって値が変わるので、cosβの値は、一定の値になるというわけではない。
【解答(その2)】
角度βが一定であることは、以下の計算でも確認できる。
式a2からa4によって、ベクトルavとbvとcvを、ベクトルaとbとcを反時計回りに90°回転したベクトルであると定義する。
ただし、この角度βは、点Aが線分BCの右側にある場合の角度であり、点Aが線分BCの左側に来ると、角度の符号が逆になる。
ひし形の対角線の直交の公式により、式a8が成り立つ。
式a7は、ベクトルavとcvがベクトルaとcに直交するベクトルであるので成り立つ。
式a11によって、tanβの値は、点Aの位置が線分BCの右側にある限り、点Aの位置によらず一定の値になる。
(解答おわり)
【問2】下図のように円周上に3点ABCがある。この場合に、以下の式1の関係が成り立つことを示せ。
【解答の方針】
(1)この問題が出たら、これは円周角の問題だと気付くことがベスト。
各ベクトルの内積と円周角との関係を示して、円周角の定理が式(1)であらわされることを示すのが一番速い解答になります。
(2)円周角の問題であると気付かなかった場合は、この問題を(問1)のように、三角関数で解くのが2番目に速く解けます。
(3)以上の2つの視点に気付かなかった場合は、以下のように地道にベクトルの計算をします。
ベクトルの計算にあたって、この問題のように難しい問題の場合は、ベクトルを互いに直交する2方向の成分に分解して成分の計算を行います。そうすれば、以下のように計算を進めることができ、問題が解けるようになります。
【解答】
式(1)の左辺を、べクトルを成分に分解して計算する。
この式(3)と(4)の結果を合わせて、式(1)の右辺を計算する。
よって式(1)が成り立つ。
(解答おわり)
リンク:
ベクトルの角度を複素数平面で計算できることを初めて知ったら試してみよう
高校数学の目次


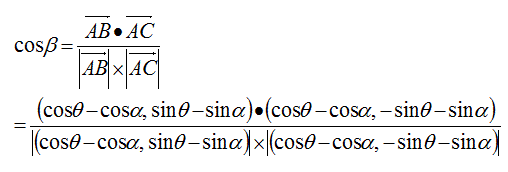



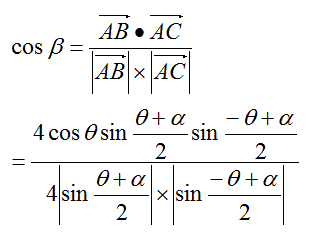





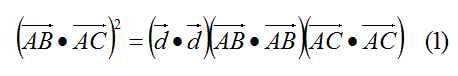




0 件のコメント:
コメントを投稿