以下の「ひし形の対角線の直交の公式」は、このページの読者の心の隅っこのどこかに残れば良いと思います。ガチガチに覚えないようにして、数学を楽しんで欲しいと思います。
読者が、この公式が必要になった時に、「たしか、そのような式がありそうな気がする」と思いだして、読者が自力でこの公式を導き出して使えたら良いと考えます。
(公式は全て、必要な時に自力で導き出して、それが使えれば良いと思います。)
【ひし形の対角線の直交の公式】
下図のひし形OAKBの2つの対角線OKとABが互いに直交することが、
以下の図の線分OKの傾きが、線分ABに平行な線分OHの傾きの逆数×(-1)である、ことにより証明できます。
【公式の証明】
(OA)2- (OB)2:
ー1/(OHの傾き)=(OKの傾き)
∴ OKとOHは直交する。
∴ OKとABは直交する。
「この式6の左右の項が互いに置き換えられる」
ということが、
ひし形の対角線の直交の公式です。
(ひし型の対角線の直交の公式おわり)
(補足)この公式を逆にして認識した方が良いかもしれない。
ひし形の対角線が互いに直交することは幾何学的に証明できます。
そして、この公式の逆の証明により、線分OKと線分ABが互いに直交する場合は:
ー1/(ABの傾き)=(OKの傾き)
となる事が証明できる。
なお、
ー1/(ABの傾き)=(OKの傾き)
となる事も、
読者が、この公式が必要になった時に、「たしか、そのような式がありそうな気がする」と思いだして、読者が自力でこの公式を導き出して使えたら良いと考えます。
(公式は全て、必要な時に自力で導き出して、それが使えれば良いと思います。)
【ひし形の対角線の直交の公式】
下図のひし形OAKBの2つの対角線OKとABが互いに直交することが、
以下の図の線分OKの傾きが、線分ABに平行な線分OHの傾きの逆数×(-1)である、ことにより証明できます。
【公式の証明】
(OA)2- (OB)2:
ー1/(OHの傾き)=(OKの傾き)
∴ OKとOHは直交する。
∴ OKとABは直交する。
「この式6の左右の項が互いに置き換えられる」
ということが、
ひし形の対角線の直交の公式です。
(ひし型の対角線の直交の公式おわり)
(補足)この公式を逆にして認識した方が良いかもしれない。
ひし形の対角線が互いに直交することは幾何学的に証明できます。
そして、この公式の逆の証明により、線分OKと線分ABが互いに直交する場合は:
ー1/(ABの傾き)=(OKの傾き)
となる事が証明できる。
なお、
ー1/(ABの傾き)=(OKの傾き)
となる事も、
以上の計算をしないでも、幾何学的に証明できます。
【ひし形の対角線の直交の公式の応用】
ひし形の対角線の直交の公式は、以下のように、ベクトルの内積の式を変換する計算に使います。
上図のベクトルに関してひし形の対角線の直交の公式は、以下の式a1又はa2であらわせます。
式a3のように、ベクトルの内積の式が、式a2を使って変換できます。
また、この式a3を使うと、以下の式a4であらわす、
任意の定数sで成り立つベクトルの内積の変換公式が作れます。
【2重平行四辺形の面積の公式】
ここで、もう1つの式7で与えられる、2重平行四辺形の面積の公式も覚えて使いましょう。
(これは、OAの長さとOBの長さが異なっても成り立つ恒等式です)
この式7の公式は、右辺から左辺を導く公式として覚えましょう。
この式7の公式は、以下の図の2重の平行四辺形の面積の大きさの関係をあらわす公式です。
(この計算は、ベクトルの外積の計算であり、並行四辺形の面積を求める計算であるという意味を持ちます。)
(2重平行四辺形の面積の公式おわり)
この2重平行四辺形の面積の公式は、ベクトルAとBを反時計回りに90度回転したベクトルAvとBvを使って、以下の式であらわせます。
リンク:
高校数学の目次
【ひし形の対角線の直交の公式の応用】
ひし形の対角線の直交の公式は、以下のように、ベクトルの内積の式を変換する計算に使います。
上図のベクトルに関してひし形の対角線の直交の公式は、以下の式a1又はa2であらわせます。
式a3のように、ベクトルの内積の式が、式a2を使って変換できます。
また、この式a3を使うと、以下の式a4であらわす、
任意の定数sで成り立つベクトルの内積の変換公式が作れます。
【2重平行四辺形の面積の公式】
ここで、もう1つの式7で与えられる、2重平行四辺形の面積の公式も覚えて使いましょう。
(これは、OAの長さとOBの長さが異なっても成り立つ恒等式です)
この式7の公式は、右辺から左辺を導く公式として覚えましょう。
この式7の公式は、以下の図の2重の平行四辺形の面積の大きさの関係をあらわす公式です。
(この計算は、ベクトルの外積の計算であり、並行四辺形の面積を求める計算であるという意味を持ちます。)
この2重平行四辺形の面積の公式は、ベクトルAとBを反時計回りに90度回転したベクトルAvとBvを使って、以下の式であらわせます。
リンク:
高校数学の目次

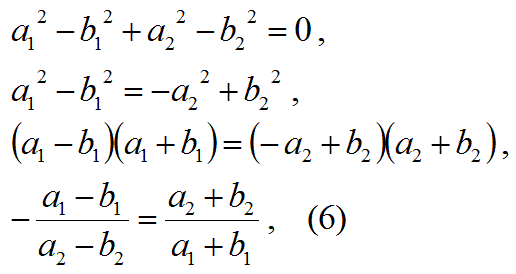

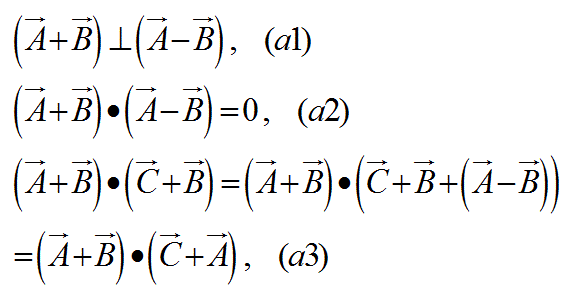

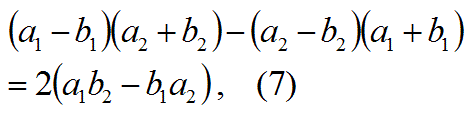


0 件のコメント:
コメントを投稿