

【問】複素数平面を利用して、座標原点の回りに回転させた楕円の方程式を求めよ。
【解答】
先ず、回転する前の楕円の方程式は以下の図のようにあらわせます。
この楕円を、以下の図のように、原点の回りに角度θ回転させます。
ここで、元の複素数zを左回りにθ回転させるには、以下の計算のように偏角θの複素数を掛け算しました。

ここで、楕円の軸方向の単位ベクトルをあらわす複素数gとhを考えます。
回転した楕円上の点を元のzから回転した位置の新しい複素数zであらわします。
新しいzは、複素数gの、(実数)x倍と、複素数hの、(実数)y倍の複素数の合成でもあらわせます。
この新しい複素数zの実数成分を(実数)x’であらわし、虚数成分を(実数)y’であらわします。
なお、xとyのあらわす楕円の式は、回転していない元の楕円の式と同じです。
回転した楕円の式は、新しい複素数zの成分のx’とy’で表した式です。
この(x’,y’)を(x,y)であらわす式は、楕円の回転角度θを使って、上の式であらわせます。
ここで、
(x,y)を(x’,y’)であらわす式と、
(x’,y’)を(x,y)であらわす式とは、
以下の式の様に、θの正負を逆にしただけの式であらわされる、
回転変換式の間の対の関係がありますので、覚えておきましょう。
この変換の式は、ここをクリックした先にある「ベクトルの回転変換」として考える方が理解し易い。
【解答】
先ず、回転する前の楕円の方程式は以下の図のようにあらわせます。

ここで、楕円の軸方向の単位ベクトルをあらわす複素数gとhを考えます。
回転した楕円上の点を元のzから回転した位置の新しい複素数zであらわします。
新しいzは、複素数gの、(実数)x倍と、複素数hの、(実数)y倍の複素数の合成でもあらわせます。
この新しい複素数zの実数成分を(実数)x’であらわし、虚数成分を(実数)y’であらわします。
なお、xとyのあらわす楕円の式は、回転していない元の楕円の式と同じです。
回転した楕円の式は、新しい複素数zの成分のx’とy’で表した式です。
この(x’,y’)を(x,y)であらわす式は、楕円の回転角度θを使って、上の式であらわせます。
ここで、
(x,y)を(x’,y’)であらわす式と、
(x’,y’)を(x,y)であらわす式とは、
以下の式の様に、θの正負を逆にしただけの式であらわされる、
回転変換式の間の対の関係がありますので、覚えておきましょう。
この変換の式は、ここをクリックした先にある「ベクトルの回転変換」として考える方が理解し易い。
この変換式を使って、
(x,y)であらわされた楕円の式を(x’,y’)で書き換えた式が、求める回転した楕円の式です。
これは、正確な計算で求めますが、
計算間違いを少なくするため、問題を単純化した場合を考えて、単純な場合の計算結果と食い違う計算ミスが無いかをチェックしながら、以下のように計算した方が良いです。
そのために、上の図のように、bが十分小さい扁平な楕円の場合を計算します。
bが十分小さいならば、yは限りなく0に近づきます。
そして、(扁平な楕円なので) 以下の式のように、y’がx’に比例します。
以下では、この扁平な楕円の場合の条件から外れた結果が出る誤りが混じる事がないかチェックしながら、式を注意深く変形していきます。
これで、回転した楕円の式が得られました。
以下で、この楕円の式が、bが限りなく0に近い扁平な楕円の場合も妥当な結果を与えるかチェックします。
以上で得られた楕円の方程式は、bが十分小さい扁平な楕円の場合と矛盾しない結果が得られた。
そのため、以上の計算には計算ミスが混入しなかったと安心できます。
得られた楕円の式を以下に整理して書きます。
回転した楕円の式を整理すると、回転した楕円の式の係数を使うと、上の式のように、楕円の軸の回転角度θの2倍のタンジェントが得られる関係があることがわかりました。
(補足)
楕円の軸の回転角度θを与えるこの式は、何度おぼえても忘れます。その忘れ対策として、この式を以下の様にして素早く導き出しましょう。
先ず、上の図を思い描きます。
極座標で表した動径rが最大または最小になる角度α=θです。
そのため、以下のようにして動径rの微分の式を作ります。
この式2の微分をf(α)の式に行います。
この式4が求める回転角θを与える式です。
リンク:
(x,y)であらわされた楕円の式を(x’,y’)で書き換えた式が、求める回転した楕円の式です。
これは、正確な計算で求めますが、
計算間違いを少なくするため、問題を単純化した場合を考えて、単純な場合の計算結果と食い違う計算ミスが無いかをチェックしながら、以下のように計算した方が良いです。
そのために、上の図のように、bが十分小さい扁平な楕円の場合を計算します。
bが十分小さいならば、yは限りなく0に近づきます。
そして、(扁平な楕円なので) 以下の式のように、y’がx’に比例します。
以下では、この扁平な楕円の場合の条件から外れた結果が出る誤りが混じる事がないかチェックしながら、式を注意深く変形していきます。
これで、回転した楕円の式が得られました。
以下で、この楕円の式が、bが限りなく0に近い扁平な楕円の場合も妥当な結果を与えるかチェックします。
そのため、以上の計算には計算ミスが混入しなかったと安心できます。
得られた楕円の式を以下に整理して書きます。
回転した楕円の式を整理すると、回転した楕円の式の係数を使うと、上の式のように、楕円の軸の回転角度θの2倍のタンジェントが得られる関係があることがわかりました。
(補足)
楕円の軸の回転角度θを与えるこの式は、何度おぼえても忘れます。その忘れ対策として、この式を以下の様にして素早く導き出しましょう。
先ず、上の図を思い描きます。
極座標で表した動径rが最大または最小になる角度α=θです。
そのため、以下のようにして動径rの微分の式を作ります。
リンク:


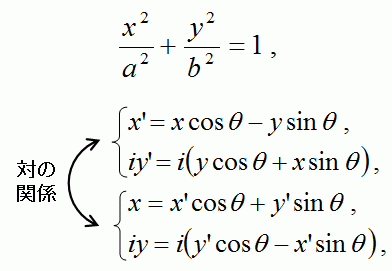
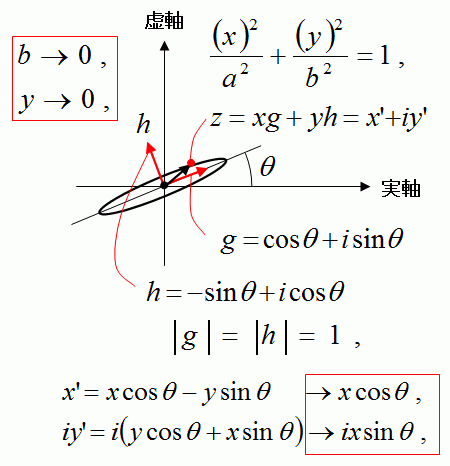








0 件のコメント:
コメントを投稿