【難問】以下の不定方程式の整数解をすべて求めよ。
(コメント)この問題は、ペル方程式で解くこともできない。
とても難問です。


すなわち、この式が成り立つには、nが5の倍数5pである必要がある。
1つの解は見つけた。
この問題は、海外のインターネットで議論されていて、
それ以外の解も求められている。
(x,y)=(1541,-1822)
も解であり、
それ以外にも解がありますが、
解の個数は有限のようです。
そのインターネットのサイトには、
簡単な構造の漸化式により、
1つの解から、他の解が得られると書いてありました。
ただし、そのサイトの漸化式は間違っていましたので、
正しい漸化式を計算して記録に残すことにします。
とりあえず、1つの解を得た場合に他の解を求める漸化式を作ってみます。
この式の解の漸化式を1つ作ります。
この式と整数解を求めるx,yとの関係を以下に整理しておきます。
作成する漸化式は、以下の式を満たす漸化式にします。
1つの解uが得られた場合に他の解Uを与える漸化式を、行列Mを使った式11で定義します。
式5’を扱い易くするために、その係数を以下の行列の要素aで定義します。
この式に、先の式11を代入して、以下のようにして、行列Mの要素の満たす式を求める。
この式の左右の項の行列を計算する。
この式を満たす行列は以下の式で与えられる。cとdは選択の自由度を与える未知数である。
この式を満足するcとdの整数解を1つ、以下の様に求め、それを使って、行列Mを定める。
これで、1つの漸化式の行列Mが得られた。
この漸化式を使って、以下のように問題を解析し、この漸化式の有効性を調べる。
先に求めた解
(s,t)=(16,5)
に、この漸化式を適用する。
上のように、この漸化式を使って(s、t)=(u1,u2)の解を順次に計算したが、その解の(u1,u2)の組に対する(x,y)が整数になる解が直ぐにはみつからなかった。
次に、以下の(s、t)=(u1,u2)の組を求めて、この漸化式を適用して他の解を得て(x,y)の整数解を探した。
以上のように1つの整数解(x,y)の組(1541,-1822)がみつかった。
更に、以下の(s、t)=(u1,u2)の組を求めて、この漸化式を適用して他の解を得て(x,y)の整数解を探した。
以上のように1つの整数解(x,y)の組(-40119,-64312)がみつかった。
以上の計算の結果、この漸化式は、解を探すのにある程度役に立った。
先のサイトに書いてあった解を見ると、以上の探索により得た解は、小さな値の解を漏らさず探索できていた。
そのため、この漸化式は結構役にたっていることがわかった。
以上でいくつかの解が得られた。
次に、全ての解を網羅する漸化式があるのかどうか、以上の解を使って調べてみる。
(解答途中)
リンク:
高校数学の目次
(コメント)この問題は、ペル方程式で解くこともできない。
とても難問です。
【解答】(途中までの速報)


すなわち、この式が成り立つには、nが5の倍数5pである必要がある。
この問題は、海外のインターネットで議論されていて、
それ以外の解も求められている。
(x,y)=(1541,-1822)
も解であり、
それ以外にも解がありますが、
解の個数は有限のようです。
そのインターネットのサイトには、
簡単な構造の漸化式により、
1つの解から、他の解が得られると書いてありました。
ただし、そのサイトの漸化式は間違っていましたので、
正しい漸化式を計算して記録に残すことにします。
とりあえず、1つの解を得た場合に他の解を求める漸化式を作ってみます。
この式の解の漸化式を1つ作ります。
この式と整数解を求めるx,yとの関係を以下に整理しておきます。
作成する漸化式は、以下の式を満たす漸化式にします。
1つの解uが得られた場合に他の解Uを与える漸化式を、行列Mを使った式11で定義します。
式5’を扱い易くするために、その係数を以下の行列の要素aで定義します。
この式に、先の式11を代入して、以下のようにして、行列Mの要素の満たす式を求める。
この式の左右の項の行列を計算する。
この式を満たす行列は以下の式で与えられる。cとdは選択の自由度を与える未知数である。
この式を満足するcとdの整数解を1つ、以下の様に求め、それを使って、行列Mを定める。
これで、1つの漸化式の行列Mが得られた。
この漸化式を使って、以下のように問題を解析し、この漸化式の有効性を調べる。
先に求めた解
(s,t)=(16,5)
に、この漸化式を適用する。
上のように、この漸化式を使って(s、t)=(u1,u2)の解を順次に計算したが、その解の(u1,u2)の組に対する(x,y)が整数になる解が直ぐにはみつからなかった。
次に、以下の(s、t)=(u1,u2)の組を求めて、この漸化式を適用して他の解を得て(x,y)の整数解を探した。
更に、以下の(s、t)=(u1,u2)の組を求めて、この漸化式を適用して他の解を得て(x,y)の整数解を探した。
以上のように1つの整数解(x,y)の組(-40119,-64312)がみつかった。
以上の計算の結果、この漸化式は、解を探すのにある程度役に立った。
先のサイトに書いてあった解を見ると、以上の探索により得た解は、小さな値の解を漏らさず探索できていた。
そのため、この漸化式は結構役にたっていることがわかった。
以上でいくつかの解が得られた。
次に、全ての解を網羅する漸化式があるのかどうか、以上の解を使って調べてみる。
(解答途中)
リンク:
高校数学の目次



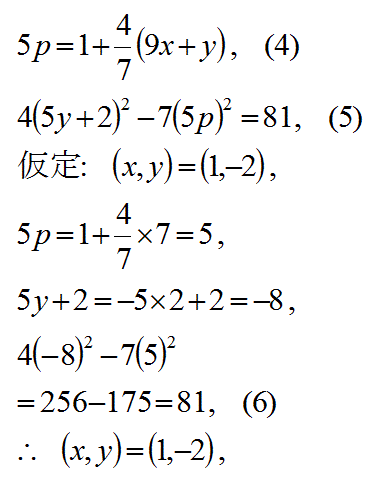












返信削除楕円上のすべての格子点を求めるほど容易な問題はない が..
誘導問題作成のプロが 以下の全ての手順(1)--(4)
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/148354014733805903179.gif
に 忠実に 従った 後 (5) 楕円∩Z^2 を 求めよ と 強制する。
↓の問題を↑の如く誘導問題にして下さい;
---------以下 が メイン です. 宜しくお願い致します--------
● 双曲線 x^2 + 4 x y - 8 y^2 - 4 y = 0 上 の
全ての格子点を(導出法を明記し)お願い致します;
漸化式により、1つの解から、他の解が得られるなら
漸化式の導出方法をも明記下さい;
● 双曲線 x^2 + 4 x y - 8 y^2 - 4 y = 0 の双対曲線を求め;
其の上の 全ての格子点をお願い致します;
参考の情報をどうもありがとうございます。
返信削除教えていただいた情報を良く検討してみます。