【問】(高校生の難問)
(コメント)この問題は、ペル方程式で解けます。
大学入試問題に出題されることもあるようですが、
高校生には難問ですので、理系難関大学や医学部を受験しようとしている高校3年生以外は、この問題をやらなくても良いと思います。
該当する高校生であっても、参考に見ておくだけで十分と思います。
【解1】
解のいくつかを求める。
もう1つの解を計算する。
この場合はx,yは自然数解を持たない。
もう1つの解を計算する。
これは自然数解を持つ。
次に、1つの解を得た場合に他の解を求める漸化式を作る。
作成する漸化式は、以下の式を満たす漸化式にします。
1つの解uが得られた場合に他の解Uを与える漸化式8を、行列Mを使った式で定義します。
式3を扱い易くするために、式3の係数を以下の行列の要素aで定義します。
以下のようにして、行列Mの要素の満たす式を求める。
この式の左右の項の行列を計算する。
この式を満たす行列は以下の式で与えられる。cとdは選択の自由度を与える未知数である。
この式を満足するcとdの整数解を1つ、以下の様に求め、それを使って、行列Mを定める。
これで、1つの漸化式の行列Mが得られた。
ペル方程式の場合は、この漸化式だけで全ての解を計算できることが分かっている。
すなわち、ペル方程式では、c+d√3の値を最小にする自然数解(c,d)=(2,1)を使って上の漸化式を作れば、その漸化式で作った解が全ての自然数解をあらわす。
(漸化式の他の導出方法)
以下のようにこの漸化式を導出する方が簡単なようです。
この漸化式を使って、解を順次に計算できるが、以下では、その計算を先回りして解をあらわす式を求める。
この式を変形して、係数zとmとを使った以下の形の式に変形する。

この式を解いてzとmを定める。

zとmが2組あることで以下の式が成り立つことを利用して解を計算する。

以下のようにk番目の解を計算する。

(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
((U1,k ,U2,k)の式を導き出す簡単な計算方法)
以下の様にすると簡単に計算できます。
(漸化式の他の導出方法)の計算を続けて、以下の計算をします。
(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
(解答おわり)
【解2】
解2では、解1によって計算するx,yの解には整数解以外の解が混在していたのを改善する。
この式B1を式2に代入する。
ここで、u1とu2には正負の何れかであるかが決まっていない自由度がある。
6y+1=1(mod3)であるので、u1=1(mod3)であるu1=か、-u1=1(mod3)である-u1を6y+1に等しいと計算する。
(後の計算で、 常に正のu1=1(mod3)であることが分かる)

この式から、以下の漸化式が得られる。
この漸化式に従うと、
順次に計算する正のu1は常に、u1=1(mod3)となることが分かる。
そのためyの整数解は、B3’のみで計算しなければならない。
一方でxの整数解は、正負のu2を使って、いずれの計算でも整数解が得られる。
この漸化式を使って、(x,y)の整数解をいくつか求めてみる。
これらの計算において、計算した(x,y)は全て整数解になったので、整数解以外の解の混在を無くすことができたと考えられる。
次に、漸化式の計算を繰り返す手順を飛び越えて、一般解をあらわす式を求める。
この一般解の式のx,yには、整数解以外の解が混在していないと考える。
リンク:
高校数学の目次
(コメント)この問題は、ペル方程式で解けます。
大学入試問題に出題されることもあるようですが、
高校生には難問ですので、理系難関大学や医学部を受験しようとしている高校3年生以外は、この問題をやらなくても良いと思います。
該当する高校生であっても、参考に見ておくだけで十分と思います。
【解1】
もう1つの解を計算する。
これは自然数解を持つ。
次に、1つの解を得た場合に他の解を求める漸化式を作る。
作成する漸化式は、以下の式を満たす漸化式にします。
1つの解uが得られた場合に他の解Uを与える漸化式8を、行列Mを使った式で定義します。
式3を扱い易くするために、式3の係数を以下の行列の要素aで定義します。
以下のようにして、行列Mの要素の満たす式を求める。
この式を満たす行列は以下の式で与えられる。cとdは選択の自由度を与える未知数である。
この式を満足するcとdの整数解を1つ、以下の様に求め、それを使って、行列Mを定める。
ペル方程式の場合は、この漸化式だけで全ての解を計算できることが分かっている。
すなわち、ペル方程式では、c+d√3の値を最小にする自然数解(c,d)=(2,1)を使って上の漸化式を作れば、その漸化式で作った解が全ての自然数解をあらわす。
(漸化式の他の導出方法)
以下のようにこの漸化式を導出する方が簡単なようです。
この漸化式を使って、解を順次に計算できるが、以下では、その計算を先回りして解をあらわす式を求める。
この式を変形して、係数zとmとを使った以下の形の式に変形する。

この式を解いてzとmを定める。

zとmが2組あることで以下の式が成り立つことを利用して解を計算する。

以下のようにk番目の解を計算する。

(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
((U1,k ,U2,k)の式を導き出す簡単な計算方法)
以下の様にすると簡単に計算できます。
(漸化式の他の導出方法)の計算を続けて、以下の計算をします。
(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
(解答おわり)
【解2】
解2では、解1によって計算するx,yの解には整数解以外の解が混在していたのを改善する。
この式B1を式2に代入する。
ここで、u1とu2には正負の何れかであるかが決まっていない自由度がある。
6y+1=1(mod3)であるので、u1=1(mod3)であるu1=か、-u1=1(mod3)である-u1を6y+1に等しいと計算する。
(後の計算で、 常に正のu1=1(mod3)であることが分かる)

この式から、以下の漸化式が得られる。
この漸化式に従うと、
順次に計算する正のu1は常に、u1=1(mod3)となることが分かる。
そのためyの整数解は、B3’のみで計算しなければならない。
一方でxの整数解は、正負のu2を使って、いずれの計算でも整数解が得られる。
この漸化式を使って、(x,y)の整数解をいくつか求めてみる。
これらの計算において、計算した(x,y)は全て整数解になったので、整数解以外の解の混在を無くすことができたと考えられる。
次に、漸化式の計算を繰り返す手順を飛び越えて、一般解をあらわす式を求める。
この一般解の式のx,yには、整数解以外の解が混在していないと考える。
リンク:
高校数学の目次
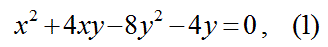







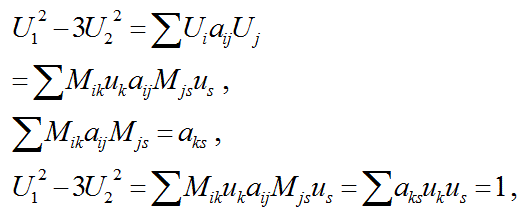










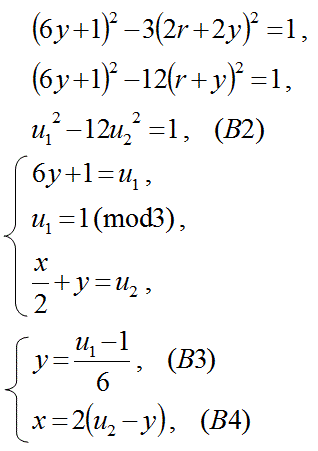






f[x, y] = x^2 + 4*x*y - 8*y^2 - 4*y でf[3,-1]=-7 で B'z Zero がイイ とならず.....(youtube B'z Zero)
返信削除ご指摘をどうもありがとうございました。
返信削除計算書違いをしていましたので、ページ本文の計算間違いを直して書き直しました。
有難う御座います。
返信削除7 x^2 + 200 x y + 96 x + 25 y^2 + 24 y + 11 = 0 なら如何でしょうか?
7 x^2 + 200 x y + 96 x + 25 y^2 + 24 y + 11 = 0
返信削除は難しい。整数解が存在しないのではないかとも考えましたが、整数解が存在にないという証明試みがはじかれています。かと言って、整数解も見つけられないでいます。
きちんと整数論の教科書を読んで、基礎を固めて地道に行くしかないのではないかとも思います。
返信削除整数や有理数問題が 流行ってる らしい。[永遠に廃れることはない]
↓の (5)の問題を誘導(1)-(4)に 素直に 従い 命じられるままに
「 解けてしまった」 人は多いにちがいない...
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/148582533601630581180.gif
(5)の 二次曲線 C; 6*x^2+20*x*y+17*y^2=59 視るや否や 少女 A が
「Cのもとで yの最小値,最大値を求め
□ C が 箱入り 状況にある故
Table[{1/6 (-10 y+Sqrt[2] Sqrt[177-y^2]),y},{y,-14,14}]
等し 即座に 4組 の格子点を獲たぁ-」 と云う。
(5) を まっ先に視れば 世界のだれもが
A を イの一番に 定義する! のは 明らか。
Bをみてしまったので Bの【出所・出処 を明らかにする】
義務があります! ので願います;
https://www.youtube.com/watch?v=-hxKstxplBk
https://www.youtube.com/watch?v=ZAjp9YnATIU&list=RDZAjp9YnATIU#t=21
馴れ親しんだ 係数 の 低次曲線
6 x^2+9 x y+19 y^2=1000 について
誘導問題創作者に倣い (1) KARA (5) を作成し
特に B に相当する行列を 明記し
すべて 解いて 今後この手法を 駆使したいか 否か を 記して下さい。
また 少女A にならい xの最小値=_____ 最大値=____ を 求め
瞬時に格子点達を求めてください;
6 x^2+9 x y+19 y^2=1000 の 双対曲線を求め
その上の格子点を探求願います;
https://www.youtube.com/watch?v=kEbFTYJbgZ0
(超易なケースです)
返信削除世間では 「楕円の哲学」,「楕円の教育学」 なる概念を定義し
信奉されて おられる 方が 多いようだ ..........;
http://holisticeducation2011.blogspot.jp/2016/03/2016322.html#!/2016/03/2016322.html
http://www3.gimmig.co.jp/hanada/yuji.html
http://www.sasayama.or.jp/diary/2002jun24.htm
「双曲線の哲学」,「双曲線の教育学」 なる概念 を定義し
布教される 人も 出現しそうである。
ところで 「楕円」と 「双曲線」は 議論すれば パラレルに行く
ことは 世界の殆どすべての人が 疑わない 筈。
ところが 最近 「未だ低次曲線で 苦悩しておるのかっ!」 と
嗤われそうな 事例に 幾度か遭遇した。
楕円上の格子点の問題の方 は 誘導問題作成のプロが
以下の全ての手順(1)--(4)
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/148354014733805903179.gif
に 忠実に 従った 後 (5) 楕円∩Z^2 を 求めよ と 強制する。
が 右下の如く「箱入り娘」法で 実に 容易に とける。
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/148582533601630581180.gif
■ 双曲線上のすべての格子点を求める際 は
容易過ぎる ケース と 極めて困難な ケースが
ある ことに 最近 遭遇し 解くようお願い中であります。
さて このように「2次曲線なる低次曲線に関する問題を
まだ 解こうと苦悩しているのか」と 嗤う人が 存在するでしょう。
で 高次代数曲線に 関する問題を提起しますので解いて下さい;
c1; 7 x^16 + 70 x^14 y^2 - 50 x^14 + 385 x^12 y^4 - 128 x^12 y^2 +
129 x^12 + 1120 x^10 y^6 - 774 x^10 y^4 - 570 x^10 y^2 - 156 x^10 +
1939 x^8 y^8 - 3908 x^8 y^6 + 903 x^8 y^4 + 1264 x^8 y^2 + 89 x^8 +
1120 x^6 y^10 - 3908 x^6 y^8 + 4854 x^6 y^6 - 1522 x^6 y^4 -
654 x^6 y^2 - 18 x^6 + 385 x^4 y^12 - 774 x^4 y^10 + 903 x^4 y^8 -
1522 x^4 y^6 + 993 x^4 y^4 + 16 x^4 y^2 - x^4 + 70 x^2 y^14 -
128 x^2 y^12 - 570 x^2 y^10 + 1264 x^2 y^8 - 654 x^2 y^6 +
16 x^2 y^4 + 2 x^2 y^2 + 7 y^16 - 50 y^14 + 129 y^12 - 156 y^10 +
89 y^8 - 18 y^6 - y^4=0
の 双対曲線c1^★ は ↓に なることを多様な発想で導出願います;
c2; x^8 - 4 x^6 y^2 + 20 x^6 + 6 x^4 y^4 + 108 x^4 y^2 - 50 x^4 -
4 x^2 y^6 + 108 x^2 y^4 - 140 x^2 y^2 + 36 x^2 + y^8 + 20 y^6 -
50 y^4 + 36 y^2 - 7=0
二重根号問題を 出題したがる 教員は 昔から存在したようです。
曲線 C; Sqrt[1 - Sqrt[1 - x^2]] + Sqrt[1 - Sqrt[1 - y^2]] = 1
を 真部分集合とする 最小の代数多様は c2 であることを示して下さい;
その様子 C⊂c2 を 描写願います。
2重接線問題に ついて XJAPAN が コタエテ ゐる;
https://www.physicsforums.com/threads/finding-the-equation-of-a-bitangent-line-to-a-curve.868433/
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/148475134078075794177.gif
<---- 「双対曲線ってなんだっ!」 と 云われる方に。
此処に 双対曲線の定義があります・
此れに 倣い c1の 2重接線達をc1^★の特異点達を求め 導出願います;
此れに 倣い c2の 2重接線達をc2^★の特異点達を求め 導出願います;
格子点を求めて下さい;
c1∩Z2 c2∩Z2
返信削除R^3 で S1; x + y + z = 2 の 君の名は 超平面。
低次曲面 S2 ; x*y + y*z + z*x = 1 の 君の名は;_______
S1∩S2 の 君の名は;_____________.
https://www.youtube.com/watch?v=HkUT8wg2ldI
S1∩S2 は 3-(1+1)=1 の 多様体で 媒介変数表示 叶い;
___________________.
S1∩S2のもとで z の 最小値 は_____, 最大値 は ______.
https://www.youtube.com/watch?v=lq6j3S_CnNg
低次曲面 S2 ; x*y + y*z + z*x = 1 の 双対曲面 S2^★を
すぐ モトメテ クダサイ;
格子点達も 求めずには イラレナイ で せう どうぞ!
S2 ∩Z^3
S2^★∩Z^3
低次曲面 S2^★ ; ___________ の 君の名は;_______
S1∩S2^★ の 君の名は;_____________.
https://www.youtube.com/watch?v=HkUT8wg2ldI
S1∩S2^★ は 3-(1+1)=1 の 多様体で 媒介変数表示 叶い;
___________________.
S1∩S2^★ のもとで z の 最小値 は_____, 最大値 は ______.
https://www.youtube.com/watch?v=lq6j3S_CnNg
http://d.hatena.ne.jp/obelisk2/20131130/1385790445
> 美男美女は、顔のパーツが全てシンメトリー(左右対称)である
返信削除>と言われるが、人間の顔だけでなく、人は左右対称な物に美を見い出す
>ものなのかもしれない。インテリアのコーディネートでも、家具を
>シンメトリーに配置すれば外れがないというが、それは、
>映画やドラマの撮影においても同じなのかもしれない , とさ;
http://rocketnews24.com/2016/09/23/803108/
ありったけの 対称美 の 在る 代数曲面 S;
81 x^12-324 x^9 y^3-324 x^9 z^3+108 x^9+486 x^6 y^6+324 x^6 y^3 z^3-108 x^6 y^3+486 x^6 z^6-108 x^6 z^3+54 x^6-324 x^3 y^9+324 x^3 y^6 z^3-108 x^3 y^6+324 x^3 y^3 z^6+1080 x^3 y^3 z^3+36 x^3 y^3-324 x^3 z^9-108 x^3 z^6+36 x^3 z^3+12 x^3+81 y^12-324 y^9 z^3+108 y^9+486 y^6 z^6-108 y^6 z^3+54 y^6-324 y^3 z^9-108 y^3 z^6+36 y^3 z^3+12 y^3+81 z^12+108 z^9+54 z^6+12 z^3+1=0
の 双対曲面 S^★ を 是非求めて下さい;
S^★∩Z^3 なる 流行りの 整数問題を 解いて;
各格子点に 対応する S の 接平面を求め
S と 共に 描写願います;
今回の双対化は ↓の講義に潜り 盗聴すれば 叶いmathか?
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/147797036598624322180.gif
(逆行列で 目的が 果たせる なる 講義)
双曲線上の格子点で 私に難解なのを お願いし 幾日か過ぎた...
返信削除■ 解決されましたら 御教示願います。
少女 A 曰く;
人は見かけによるか否かしらないが
双曲線達 は 如何?
「お願いした 上も 下 の c1,c2 も みんな 同じ 双曲線だ」
「難易度に 差が 在るなんてシンジラレナーイ! と 世間の人は云う」
(「恋愛に歳の差なんて関係ナシ」派 ∃のよう..)
c1 ; 33 x^2-30 x y+2 x-63 y^2+2 y+1=0
c2 ; 2 x^2-x y-3 x-y^2+3 y+72=0
(1) 「流行の 整数解の 問題 c1∩Z^2,c2∩Z^2 はとても容易」
c1∩Z^2=
c2∩Z^2=
お願いしたのは 難解.............
(2) 「c1 の 双対は c2=c1^★」
上の少女A の言明が 虚偽でない ことをすぐ立証願います。
今回の双対化は ↓の講義に潜り 盗聴すれば 叶いmath:
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/147797036598624322180.gif
(逆行列で 目的が 果たせる なる 講義)
双曲線なら 要求されなくても 「漸近線が在る」ので求める筈;
https://www.youtube.com/watch?v=ZQu95K4toL4
<--- 問題群 在り.
難問だった、
削除7 x^2 + 200 x y + 96 x + 25 y^2 + 24 y + 11 = 0
については、関連する問題を解いて掲載しました。
>双曲線上の格子点で 私に難解なのを お願いし 幾日か過ぎた
お願いされたのは、
c1 ; 33 x^2-30 x y+2 x-63 y^2+2 y+1=0
c2 ; 2 x^2-x y-3 x-y^2+3 y+72=0
のうちの
c2でしょうか。