

ページ内リンク:
▷絶対値で表した関数を含む合成関数の微分
▷合成関数の全ての変数の範囲の微分が合成関数の微分の公式では求められない例
以下の合成関数の微分の公式があります。
この式で、左辺のyは、
y=f(g(x))=h(x)という合成関数をあらわしています。
また、右辺の導関数(dy/dt)のyは、
y=f(t)という関数をあらわし、
公式の左辺の関数y=h(x)とは異なる関数をあらわしています。
すなわち、この合成関数の微分の公式は、
関数f(t)とg(x)があり、
その関数の合成関数の、
y=f(g(x))=h(x)
という関数を作った場合に、
f’(t)=(dy/dt)と、
g’(x)=(dt/dx)との積が、
h’(x)=(dy/ dx)になる、
という公式です。
どの関数f(t)とg(x)についても、公式の成立条件が満足されれば、公式が成り立つ、という公式です。
この公式には一定の縛り(成立条件)があります。それは、「(dy/dt)=f’(t)の有限の微分係数が存在し、(dt/dx)=g’(x)の有限の値の微分係数が存在する(微分可能)」という前提条件です。
▷絶対値で表した関数を含む合成関数の微分
▷合成関数の全ての変数の範囲の微分が合成関数の微分の公式では求められない例
以下の合成関数の微分の公式があります。
y=f(g(x))=h(x)という合成関数をあらわしています。
また、右辺の導関数(dy/dt)のyは、
y=f(t)という関数をあらわし、
公式の左辺の関数y=h(x)とは異なる関数をあらわしています。
すなわち、この合成関数の微分の公式は、
関数f(t)とg(x)があり、
その関数の合成関数の、
y=f(g(x))=h(x)
という関数を作った場合に、
f’(t)=(dy/dt)と、
g’(x)=(dt/dx)との積が、
h’(x)=(dy/ dx)になる、
という公式です。
どの関数f(t)とg(x)についても、公式の成立条件が満足されれば、公式が成り立つ、という公式です。
この公式には一定の縛り(成立条件)があります。それは、「(dy/dt)=f’(t)の有限の微分係数が存在し、(dt/dx)=g’(x)の有限の値の微分係数が存在する(微分可能)」という前提条件です。
「関数が微分可能(有限の値の確定した値の微分係数が存在する)」という意味は、
「関数が、その変数のその値に限って、その変数で微分可能であれば良く、その変数のその他の値での関数の微分可能性は関係しない」
という意味です。
《絶対値で表した関数を含む合成関数の微分》
以下の合成関数 f(x) を微分します。

この合成関数は、絶対値記号まで関数と見て絶対値記号をつけたまま微分して掛け合わせます。


(合成関数の微分おわり)
《合成関数の全ての変数の範囲の微分が合成関数の微分の公式では求められない例》
関数の微分が存在しない例として、以下の2つの図の関数:
y=f(t)
t=g(x)
の合成関数を使って、
合成関数の微分の公式の信頼性を調べてみます。
y=f(t):
(図1)
t=g(x):
(図2)
関数f(t)はt=0でtによる微分が存在しません。
そのため、t≠0の場合だけに、合成関数の微分の公式を適用します。
ここで、この問題の意図が良く分かるようにするため、この合成関数の形を下図に描きます。
y=f(g(x))=h(x):
(図3)
この合成関数h(x)の、xがー1から1までの間の関数の値は良く分からないので、点線でごまかしました。
このあいまいさが気持ち悪い人のために、関数f(t)を以下のグラフのように定義することができます。
(図4)
この場合に、関数t=g(x)は図2の関数を用いると、合成関数h(x)=f(g(x))は、以下の図5になります。
(図5)
以下で、関数f(t)の微分で、有限の確定した微分係数が存在する変数 t の定義域である、
t≠0
の場合だけに合成関数の微分の公式を適用します。
先ず、t=g(x)≠0を満足する条件の1つの、
x<-1の場合を計算します。
次に、t=g(x)≠0を満足する残りの条件の、
x>1の場合を計算します。
以上で得た結果をまとめると、
関数y=f(t)については、(dy/dt)=f’(t)の有限の微分係数が存在するtの範囲は、t≠0である範囲である。
関数t=g(x)については、xのどの値でも有限の微分係数が存在するので問題無い。
制限された範囲であるt≠0を満足するt=g(x)のxの範囲は、
x<-1 or x>1
である。
そのxの範囲内で、
合成関数の微分を計算すると、以下の結果が得られた。
(計算おわり)
(補足)
ここで、合成関数y=h(x)が図5の形になる場合に、
-1<x<1の間で
h’(x)=0
になっています。
しかし、合成関数の微分の公式では、
-1<x<1の間で
h’(x)=0
となることを導き出すことができませんでした。
このことから、
合成関数の微分の公式では、0を0で割り算することになる部分で、合成関数の一部の微分係数が計算できないことがある、
ということがわかりました。
(補足2)
以上の調査の結果を見ると、
合成関数の微分の公式の縛り(成立条件)である
「y=f(t)の微分が存在し(確定した有限値になる)、
t=g(x)の微分が存在する(確定した有限値になる)」
という前提条件は、
「式を0で割り算する計算をしてはいけない」
という計算の縛りと同じ様な意味を持っていることがわかります。
すなわち、「微分可能」という前提条件は、
「0で割り算しない場合に限る」という前提条件 、
言いかえると、
「計算の違反が無い計算に限る」という前提条件、
を加えて微分の式を書くことだと考えます。
そういう「万能の条件」を正しく組み込んで計算するならば、どの様な計算もできてしまいます。
(その条件を正しく組み込まないでその計算をまねした計算は計算違反がある誤った計算になります)
その通りに、どの様な計算もできるのが、合成関数の微分の公式やその他の公式が成り立つ根拠だと考えます。
リンク:
高校数学の目次
「関数が、その変数のその値に限って、その変数で微分可能であれば良く、その変数のその他の値での関数の微分可能性は関係しない」
という意味です。
《絶対値で表した関数を含む合成関数の微分》
以下の合成関数 f(x) を微分します。

この合成関数は、絶対値記号まで関数と見て絶対値記号をつけたまま微分して掛け合わせます。


(合成関数の微分おわり)
《合成関数の全ての変数の範囲の微分が合成関数の微分の公式では求められない例》
関数の微分が存在しない例として、以下の2つの図の関数:
y=f(t)
t=g(x)
の合成関数を使って、
合成関数の微分の公式の信頼性を調べてみます。
y=f(t):
(図1)
t=g(x):
(図2)
関数f(t)はt=0でtによる微分が存在しません。
そのため、t≠0の場合だけに、合成関数の微分の公式を適用します。
ここで、この問題の意図が良く分かるようにするため、この合成関数の形を下図に描きます。
y=f(g(x))=h(x):
(図3)
この合成関数h(x)の、xがー1から1までの間の関数の値は良く分からないので、点線でごまかしました。
このあいまいさが気持ち悪い人のために、関数f(t)を以下のグラフのように定義することができます。
この場合に、関数t=g(x)は図2の関数を用いると、合成関数h(x)=f(g(x))は、以下の図5になります。
(図5)
以下で、関数f(t)の微分で、有限の確定した微分係数が存在する変数 t の定義域である、
t≠0
の場合だけに合成関数の微分の公式を適用します。
先ず、t=g(x)≠0を満足する条件の1つの、
x<-1の場合を計算します。
次に、t=g(x)≠0を満足する残りの条件の、
x>1の場合を計算します。
以上で得た結果をまとめると、
関数y=f(t)については、(dy/dt)=f’(t)の有限の微分係数が存在するtの範囲は、t≠0である範囲である。
関数t=g(x)については、xのどの値でも有限の微分係数が存在するので問題無い。
制限された範囲であるt≠0を満足するt=g(x)のxの範囲は、
x<-1 or x>1
である。
そのxの範囲内で、
合成関数の微分を計算すると、以下の結果が得られた。
(計算おわり)
(補足)
ここで、合成関数y=h(x)が図5の形になる場合に、
-1<x<1の間で
h’(x)=0
になっています。
しかし、合成関数の微分の公式では、
-1<x<1の間で
h’(x)=0
となることを導き出すことができませんでした。
このことから、
合成関数の微分の公式では、0を0で割り算することになる部分で、合成関数の一部の微分係数が計算できないことがある、
ということがわかりました。
(補足2)
以上の調査の結果を見ると、
合成関数の微分の公式の縛り(成立条件)である
「y=f(t)の微分が存在し(確定した有限値になる)、
t=g(x)の微分が存在する(確定した有限値になる)」
という前提条件は、
「式を0で割り算する計算をしてはいけない」
という計算の縛りと同じ様な意味を持っていることがわかります。
すなわち、「微分可能」という前提条件は、
「0で割り算しない場合に限る」という前提条件 、
言いかえると、
「計算の違反が無い計算に限る」という前提条件、
を加えて微分の式を書くことだと考えます。
そういう「万能の条件」を正しく組み込んで計算するならば、どの様な計算もできてしまいます。
(その条件を正しく組み込まないでその計算をまねした計算は計算違反がある誤った計算になります)
その通りに、どの様な計算もできるのが、合成関数の微分の公式やその他の公式が成り立つ根拠だと考えます。
リンク:
高校数学の目次









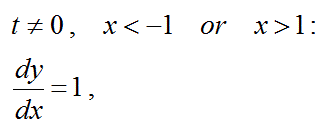
0 件のコメント:
コメントを投稿