ベクトルA(a1,a2)とB(b1,b2)の張る平行四辺形の面積Sの公式は、
S=a1b2-a2b1
で計算する公式が知られています。
この公式は思い出すのに少し時間がかかるし、何となく使いにくい感じがして、今一つ使いにくい公式のように感じました。
これに替わる、もっと楽に使えそうな公式がないかを考えました。
その結果、以下の、「長さの等しいベクトルAとBの張る2重平行四辺形の面積の公式」(後の式1から3)が導き出せました。
このような公式もあることが分かったので、この公式も速やかに導き出すことができるように、以下の公式の導き出し方を覚えてしまいましょう。

上の図で、長さの等しいベクトルAとBの張る2重平行四辺形の面積Sは、以下の式で計算できる。
よって、以下の式が成り立つ。
この式が成り立つ理由は、|A|=|B|の場合にベクトルCDとベクトルCFが直交するからです。
式1および式2は、Sの正負が反映されている公式です。
式3は、Sの絶対値をあらわす公式です。
(補足)
以上の公式は、図から求めることができた。
それらの公式のうち、式2の公式を、以下では、式を展開することで証明する。
(証明おわり)
(第2の証明)
式3の公式は、以下の図の様に、ベクトルaとベクトルbに垂直なベクトルuとベクトルwを使って証明することもできます。

これにより、以下の計算ができます。
この結果は式3の結果をあらわしている。
(証明おわり)
(第3の証明)
この2重平行四辺形の面積の公式は、ベクトルAとBを反時計回りに90度回転したベクトルAv(=u)とBv=(-w)を使って、以下の式であらわせます。
(証明おわり)
リンク:
高校数学の目次
S=a1b2-a2b1
で計算する公式が知られています。
この公式は思い出すのに少し時間がかかるし、何となく使いにくい感じがして、今一つ使いにくい公式のように感じました。
これに替わる、もっと楽に使えそうな公式がないかを考えました。
その結果、以下の、「長さの等しいベクトルAとBの張る2重平行四辺形の面積の公式」(後の式1から3)が導き出せました。
このような公式もあることが分かったので、この公式も速やかに導き出すことができるように、以下の公式の導き出し方を覚えてしまいましょう。

上の図で、長さの等しいベクトルAとBの張る2重平行四辺形の面積Sは、以下の式で計算できる。
よって、以下の式が成り立つ。
この式が成り立つ理由は、|A|=|B|の場合にベクトルCDとベクトルCFが直交するからです。
式1および式2は、Sの正負が反映されている公式です。
式3は、Sの絶対値をあらわす公式です。
(補足)
以上の公式は、図から求めることができた。
それらの公式のうち、式2の公式を、以下では、式を展開することで証明する。
(証明おわり)
(第2の証明)
式3の公式は、以下の図の様に、ベクトルaとベクトルbに垂直なベクトルuとベクトルwを使って証明することもできます。

これにより、以下の計算ができます。
この結果は式3の結果をあらわしている。
(証明おわり)
(第3の証明)
この2重平行四辺形の面積の公式は、ベクトルAとBを反時計回りに90度回転したベクトルAv(=u)とBv=(-w)を使って、以下の式であらわせます。
(証明おわり)
リンク:
高校数学の目次



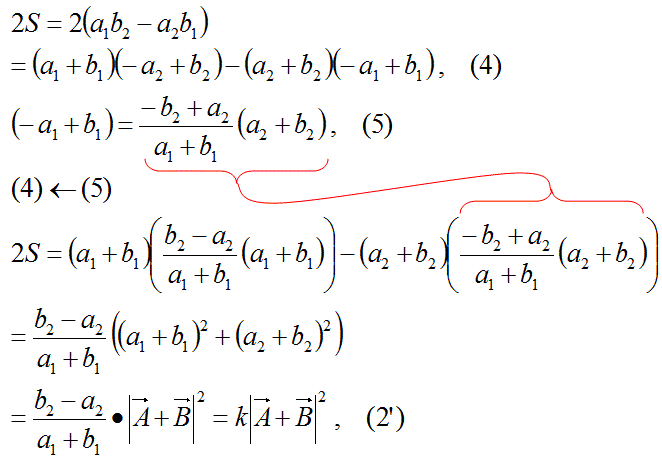

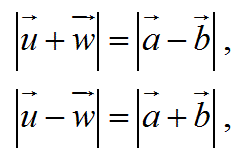


0 件のコメント:
コメントを投稿