ページ内リンク
▷ひし形の対角線の直交の第1の公式
▷ひし形の対角線のベクトル変換の公式
「ベクトルの内積の式の変形が思うようにできない」という人は、以下のベクトルの内積の公式
(この公式は、後で説明する「ひし形の対角線の直交の公式」の名前で覚えた方が覚えやすいように思います)
をおぼえて、
式の変形計算を自由にできるようになりましょう。

【ひし形の対角線の直交の第1の公式】
この公式は、下図のひし形OAKBの2つの対角線OKとABが互いに直交することを示す、ひし形の対角線の直交の公式です。
ひし形の対角線が直交するので、
以下の図の線分OKの傾きが、線分ABに平行な線分OHの傾きの逆数×(-1)になります。

【公式の証明】
ベクトルOAの成分を実数a1とa2とし、ベクトルOBの成分を実数b1とb2とする。
(OA)2-(OB)2:
ー1/(OHの傾き)=(OKの傾き)
∴ OKとOHは直交する。
∴ OKとABは直交する。
「この式6の左右の項が互いに置き換えられる」
ということが、
ひし形の対角線の直交の公式です。
(ひし型の対角線の直交の公式おわり)
【ひし形の対角線の直交の公式の応用】
ひし形の対角線の直交の公式は、以下のように、ベクトルの内積の式を変換する計算に使います。
上図のベクトルに関してひし形の対角線の直交の公式は、以下の式a1又はa2であらわせます。
式a3のように、ベクトルの内積の式が、式a2を使って変換できます。
また、この式a3を使うと、以下の式a4であらわす、
任意の定数sで成り立つベクトルの内積の変換公式が作れます。
(注意)ひし形の対角線の直交の公式は、ベクトルの絶対値が等しい場合に限り成り立ちます。この条件が成り立つ場合はあまり多くは無いので、ベクトルの内積の式を自由自在に変形するためには、この公式だけでは不十分で、その他の公式も必要です。
《ひし形の対角線のベクトル変換の公式》
また、それらのベクトルが直交するため、以下の式が成り立つ。

この式は、ベクトルの絶対値|A|=|B|の場合に成り立つ、ベクトル変換の公式です。

【ひし形の対角線の直交の公式の応用(その2)】
ひし形の対角線の直交の公式は、
下図の様に、外接円の直径を斜辺に持つ三角形が直角三角形になる事とも結びついている。
また、この図に、ベクトルの内積の変換公式を使うと、以下の公式も導くことができます。
【ひし形の対角線の直交の公式の応用(その3)】
以下のように、この公式を使って、以下の式2の公式が導けます。
ここで、ベクトルBAとベクトルCAの内積を変形します。
 ・・(式2)
・・(式2)
以上で、ベクトルの内積の式を変形した結果、外接円の中心の高さmをベクトルの内積で計算する定理(式2)が得られました。
(補足)
ここで、三角形ABCの外接円の半径をRとすると、円周角の定理が次の式1であらわされる。
cosA=m/R (1)
(この式1は、円周角の定理から素直に導き出した式であり、ベクトル計算で導こうとするととても苦労する式です。ベクトル計算の枠外で、円周角の定理から導いたこの式1を使うことで以下のベクトル計算が楽に進みました。)
また、ベクトルの内積から以下の式が得られる。
この2つの式を、先に得た、外接円の中心の高さmをベクトルの内積で計算する定理の式2に代入する。
これで得た式3は、正弦定理を使うことで速やかに導かれる式である。
この式3も、式1と同様に、ベクトルを変換する公式として利用することで、ベクトルの式の変形の自由度が増すと考える。
リンク:
円の極の座標の解の変換
高校数学の目次
▷ひし形の対角線の直交の第1の公式
▷ひし形の対角線のベクトル変換の公式
「ベクトルの内積の式の変形が思うようにできない」という人は、以下のベクトルの内積の公式
(この公式は、後で説明する「ひし形の対角線の直交の公式」の名前で覚えた方が覚えやすいように思います)
をおぼえて、
式の変形計算を自由にできるようになりましょう。

【ひし形の対角線の直交の第1の公式】
この公式は、下図のひし形OAKBの2つの対角線OKとABが互いに直交することを示す、ひし形の対角線の直交の公式です。
ひし形の対角線が直交するので、
以下の図の線分OKの傾きが、線分ABに平行な線分OHの傾きの逆数×(-1)になります。

【公式の証明】
ベクトルOAの成分を実数a1とa2とし、ベクトルOBの成分を実数b1とb2とする。
(OA)2-(OB)2:
ー1/(OHの傾き)=(OKの傾き)
∴ OKとOHは直交する。
∴ OKとABは直交する。
「この式6の左右の項が互いに置き換えられる」
ということが、
ひし形の対角線の直交の公式です。
(ひし型の対角線の直交の公式おわり)
【ひし形の対角線の直交の公式の応用】
ひし形の対角線の直交の公式は、以下のように、ベクトルの内積の式を変換する計算に使います。
上図のベクトルに関してひし形の対角線の直交の公式は、以下の式a1又はa2であらわせます。
式a3のように、ベクトルの内積の式が、式a2を使って変換できます。
また、この式a3を使うと、以下の式a4であらわす、
任意の定数sで成り立つベクトルの内積の変換公式が作れます。
(注意)ひし形の対角線の直交の公式は、ベクトルの絶対値が等しい場合に限り成り立ちます。この条件が成り立つ場合はあまり多くは無いので、ベクトルの内積の式を自由自在に変形するためには、この公式だけでは不十分で、その他の公式も必要です。
《ひし形の対角線のベクトル変換の公式》
また、それらのベクトルが直交するため、以下の式が成り立つ。

この式は、ベクトルの絶対値|A|=|B|の場合に成り立つ、ベクトル変換の公式です。

【ひし形の対角線の直交の公式の応用(その2)】
ひし形の対角線の直交の公式は、
下図の様に、外接円の直径を斜辺に持つ三角形が直角三角形になる事とも結びついている。
また、この図に、ベクトルの内積の変換公式を使うと、以下の公式も導くことができます。
【ひし形の対角線の直交の公式の応用(その3)】
以下のように、この公式を使って、以下の式2の公式が導けます。
ここで、ベクトルBAとベクトルCAの内積を変形します。
 ・・(式2)
・・(式2)以上で、ベクトルの内積の式を変形した結果、外接円の中心の高さmをベクトルの内積で計算する定理(式2)が得られました。
(補足)
ここで、三角形ABCの外接円の半径をRとすると、円周角の定理が次の式1であらわされる。
cosA=m/R (1)
(この式1は、円周角の定理から素直に導き出した式であり、ベクトル計算で導こうとするととても苦労する式です。ベクトル計算の枠外で、円周角の定理から導いたこの式1を使うことで以下のベクトル計算が楽に進みました。)
また、ベクトルの内積から以下の式が得られる。
この2つの式を、先に得た、外接円の中心の高さmをベクトルの内積で計算する定理の式2に代入する。
この式3も、式1と同様に、ベクトルを変換する公式として利用することで、ベクトルの式の変形の自由度が増すと考える。
リンク:
円の極の座標の解の変換
高校数学の目次
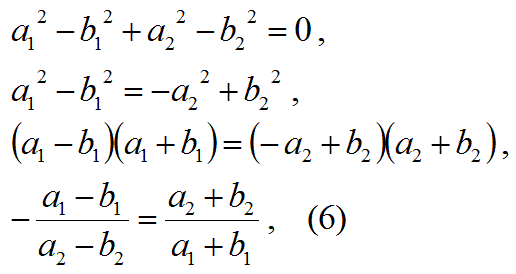

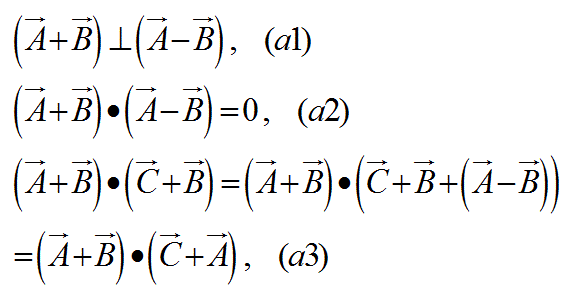

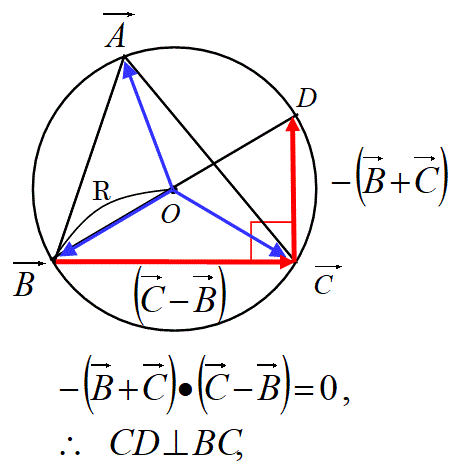




0 件のコメント:
コメントを投稿