【三平方の定理】
上図の直角三角形で、式0であらわされた三平方の定理が成り立ちます。
【拡張三平方の定理】
上図の三角形で、式1であらわされた拡張三平方の定理が成り立ちます。
a1が小さくなって0になれば、この式1は式0に一致します。
(証明開始)
三角形ABCに関して、三角形の辺の二乗の引き算の公式を使うと、以下の式が成り立ちます。
(証明おわり)
式の対称性から、以下の様に、この式は、他の式でも表現できる、複数の式があるというバラエティがあります。
すなわち:
(1)辺BCの長さaと、辺BC上への辺BAの射影の長さa1の積を使う表現。
(2)辺BAの長さcと、辺BA上への辺BCの射影の長さc1の積を使う表現。
との2つのバラエティがあります。
その式のバラエティは、ベクトルの内積を使った1つの式で表現できます。
そして、その式は、余弦定理をあらわします。
(補足)
拡張三平方の定理の式の2つの式のバラエティは、下図のように、三角形ABCの辺ACの中点を中心にした円を使った方ベきの定理から理解できます。
しかし、2つの式のバラエティを含む定理は、方ベきの定理だけでは無く、以下の定理も、そのバラエティを含むので、頭を柔らかくしましょう。
リンク:
高校数学の目次
【拡張三平方の定理】
a1が小さくなって0になれば、この式1は式0に一致します。
(証明開始)
三角形ABCに関して、三角形の辺の二乗の引き算の公式を使うと、以下の式が成り立ちます。
式の対称性から、以下の様に、この式は、他の式でも表現できる、複数の式があるというバラエティがあります。
(1)辺BCの長さaと、辺BC上への辺BAの射影の長さa1の積を使う表現。
(2)辺BAの長さcと、辺BA上への辺BCの射影の長さc1の積を使う表現。
との2つのバラエティがあります。
その式のバラエティは、ベクトルの内積を使った1つの式で表現できます。
そして、その式は、余弦定理をあらわします。
(補足)
拡張三平方の定理の式の2つの式のバラエティは、下図のように、三角形ABCの辺ACの中点を中心にした円を使った方ベきの定理から理解できます。
しかし、2つの式のバラエティを含む定理は、方ベきの定理だけでは無く、以下の定理も、そのバラエティを含むので、頭を柔らかくしましょう。
リンク:
高校数学の目次




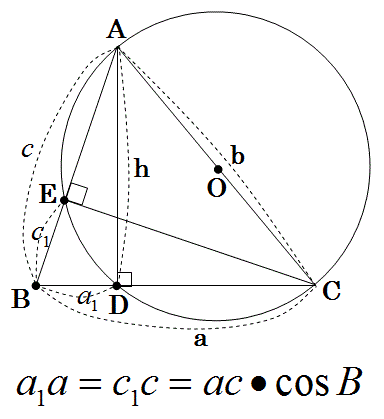

0 件のコメント:
コメントを投稿