以下の不定積分は初等関数では表せません。
上の形の関数については、
「かろうじて初等関数で表される積分」や、
「かろうじて初等関数で表される積分(その2)」
のページに、もう少し詳しく説明しました。
不定積分が初等関数で表せるためには、初等関数の関数を微分して作れる関数のグループに被積分関数が属していなければなりません。
そういう微分で作れる関数から外れた形の関数は、その不定積分が初等関数で表わせません。
不定積分が初等関数で表せる方がむしろ特殊な場合であって、不定積分が初等関数で表せない方が一般的であると考えます。
以下に、それらの、初等関数では表せない不定積分の一覧を示します。

(注意)以下の特殊な形の関数の不定積分は初等関数で表せます。
初等関数で表せない不定積分のリストを続けます。

その他、比較的単純な形の被積分関数は、ここをクリックした先のサイトに式を設定して計算すると、不定積分が初等関数で表せるか否かがわかります。
上の形の関数については、
「かろうじて初等関数で表される積分」や、
「かろうじて初等関数で表される積分(その2)」
のページに、もう少し詳しく説明しました。
不定積分が初等関数で表せるためには、初等関数の関数を微分して作れる関数のグループに被積分関数が属していなければなりません。
そういう微分で作れる関数から外れた形の関数は、その不定積分が初等関数で表わせません。
不定積分が初等関数で表せる方がむしろ特殊な場合であって、不定積分が初等関数で表せない方が一般的であると考えます。
以下に、それらの、初等関数では表せない不定積分の一覧を示します。

(注意)以下の特殊な形の関数の不定積分は初等関数で表せます。
初等関数で表せない不定積分のリストを続けます。

その他、比較的単純な形の被積分関数は、ここをクリックした先のサイトに式を設定して計算すると、不定積分が初等関数で表せるか否かがわかります。
不定積分が初等関数で表せるためには、初等関数の関数を微分して作れる関数のグループに被積分関数が属していなければなりません。
そういう微分で作れる関数から外れた形の関数は積分結果が初等関数で表わせません。
(事例1)
例えば、以下の様に初等関数を微分した関数を作れますが、その関数の各項は、他の関数の微分を組み合わせても作れ無いので、単独の各項の不定積分は初等関数で表せない。
この事例では、微分した項に不定積分すべき被積分関数に特徴的な部分のlog(x)が含まれるように原始関数Fを設定した。それが得られる原始関数はごく少数に限定されている。その原始関数を微分して、不定積分すべき被積分関数の項と、他の項を含む式を得た。
そうするために使える原始関数が少ないので、それらの原始関数を全て組み合わせても、不定積分すべき被積分関数だけが微分で得られる原始関数が存在しない。すなわち、不定積分を初等関数で表す原始関数が存在し無い事が比較的容易に判定できる。
(事例2)
xsin(x)は不定積分が初等関数で表わせます。この関数の不定積分が初等関数で表わせる理由は、xcos(x)という関数があって、その関数の三角関数のcos(x)を微分してsin(x)にしてxsin(x)という項が得られる。それ以外の微分は、xを微分して定数にしてxが消えてcos(x)という項が得られ、そのcos(x)には、sin(x)という不定積分が別にあって、sin(x)の微分がそのcos(x)を打ち消す事ができるからです。
そのため、xsin(x)は不定積分が初等関数で表わせます。
以下の関係で互いが生んだ微分を打ち消す他の相棒の初等関数がある場合も、その微分で得る複数項のうちの1つの項だけを微分で生じる事が出来る複数の項からなる関数がある。
しかし、
sin(x)/x
は不定積分が初等関数であらわせません。
その理由は、(1/x)がsin(x) に掛かった初等関数が、それを微分した結果のいくつかの項の1つ(sin(x)を残した)が、
(1/x)sin(x)
にできる関数はありますが、その関数は、
(log(x))sin(x)
という、sin(x)掛ける対数関数という、複雑な関数です。
その関数を微分した結果の項の、(1/x)sin(x)の項以外の項のsin(x)を微分して得た項は、
(log(x))cos(x)
という複雑な形の、また消すべき新たな関数を生じてしまいます。
結局、(xの関数)掛ける(三角関数の関数)という初等関数の和では、その関数を微分した項の総和が、
log(x)等の複雑なxの関数が消えた、
(1/x)sin(x)
だけ、
になる関数が無い。
そのため、
(1/x)sin(x)
は不定積分が初等関数で表わせません。
また、
x/sin(x)
も不定積分が初等関数で表わせません。
その理由は、(1/sin(x))がxに掛かった初等関数が、それを微分した結果のいくつかの項の1つ(xを残した項)が、
x/sin(x)
にできる関数はありますが、その関数は
xlog(tan(x/2))
という、x掛ける(三角関数の対数関数)といった複雑な関数です。
その関数を微分した結果の、x/sin(x)の項以外の、xを微分して消した項は、
log(tan(x/2))
という複雑な関数になってしまいます。
その関数の不定積分は初等関数では表わせず、すなわち、別の初等関数を微分してlog(tan(x/2))にすることができない。
そのため、この複雑な関数は別の初等関数の微分によっては打ち消す事ができません。
結局、(xの関数)掛ける(三角関数の関数)という初等関数の多数の項の総和で表したどんな関数でも、
その関数の微分結果の各項にlog(tan(x/2))等の複雑な関数が出ても、各項同士でそれらが打ち消し合って消えて、
x/sin(x)
だけ、
になるというような関数が無い。
そのため、
x/sin(x)
は不定積分が初等関数で表わせません。
ましてや、
1/{(x)sin(x)}
といった、
1/sin(x)という三角関数の有理関数の項に、(1/x)といった、その関数(1/x)を微分して定数にすることもできない関数を掛け算した関数は、
(xの関数)掛ける(三角関数の関数)という初等関数の多数の項の総和でどんな関数を作っても、
その関数の各項の微分結果にlog(x)等のxの関数と三角関数の積や、log(tan(x/2))等の三角関数の複雑な関数とxの関数の積が出る。それらの複雑な関数が一時的なもので各項同士で打ち消し合って消えるということは無い。
そのため、そのような多数の項の関数を微分しても、
1/{(x)sin(x)}
だけ、
になる関数が無いと考えます。
そのため、
1/{(x)sin(x)}
は不定積分が初等関数では表せないと考えます。
ただし、この事例の様な、関係する原始関数を全部網羅して不定積分が初等関数で表せない事を判定する方法は、関係する原始関数が少ない場合にのみ有効な方法です。
「かろうじて初等関数で表される積分」
に記載した形の被積分関数の積分を判定するのには向いていないので、注意が必要です。
(事例3)
以下の関数を微分して得た各項は、他の関数の微分を組み合わせることでは作れないので、単独の各項の不定積分は初等関数で表せない。
(事例4)
以下の関数を微分して得た各項も、他の関数の微分を組み合わせることでは作れないので、単独の各項の不定積分は初等関数で表せない。
以上の事例のように、被積分関数が複雑化すれば、その複雑な被積分関数を含む式が微分で得られる原始関数の数が少なくなる。
そのため、その原始関数を全て組み合わせても、微分すると被積分関数が単独で得られる原始関数が無い可能性が高くなる。すなわち、不定積分が初等関数で表されない可能性が高くなる。
リンク:
高校数学の目次
『楕圓函數論』竹内 端三 著の現代仮名遣い版

ラインセグメント日記2017年11月21日『楕円函数論』の現代語訳
そういう微分で作れる関数から外れた形の関数は積分結果が初等関数で表わせません。
(事例1)
例えば、以下の様に初等関数を微分した関数を作れますが、その関数の各項は、他の関数の微分を組み合わせても作れ無いので、単独の各項の不定積分は初等関数で表せない。
この事例では、微分した項に不定積分すべき被積分関数に特徴的な部分のlog(x)が含まれるように原始関数Fを設定した。それが得られる原始関数はごく少数に限定されている。その原始関数を微分して、不定積分すべき被積分関数の項と、他の項を含む式を得た。
そうするために使える原始関数が少ないので、それらの原始関数を全て組み合わせても、不定積分すべき被積分関数だけが微分で得られる原始関数が存在しない。すなわち、不定積分を初等関数で表す原始関数が存在し無い事が比較的容易に判定できる。
(事例2)
xsin(x)は不定積分が初等関数で表わせます。この関数の不定積分が初等関数で表わせる理由は、xcos(x)という関数があって、その関数の三角関数のcos(x)を微分してsin(x)にしてxsin(x)という項が得られる。それ以外の微分は、xを微分して定数にしてxが消えてcos(x)という項が得られ、そのcos(x)には、sin(x)という不定積分が別にあって、sin(x)の微分がそのcos(x)を打ち消す事ができるからです。
そのため、xsin(x)は不定積分が初等関数で表わせます。
以下の関係で互いが生んだ微分を打ち消す他の相棒の初等関数がある場合も、その微分で得る複数項のうちの1つの項だけを微分で生じる事が出来る複数の項からなる関数がある。
しかし、
sin(x)/x
は不定積分が初等関数であらわせません。
その理由は、(1/x)がsin(x) に掛かった初等関数が、それを微分した結果のいくつかの項の1つ(sin(x)を残した)が、
(1/x)sin(x)
にできる関数はありますが、その関数は、
(log(x))sin(x)
という、sin(x)掛ける対数関数という、複雑な関数です。
その関数を微分した結果の項の、(1/x)sin(x)の項以外の項のsin(x)を微分して得た項は、
(log(x))cos(x)
という複雑な形の、また消すべき新たな関数を生じてしまいます。
結局、(xの関数)掛ける(三角関数の関数)という初等関数の和では、その関数を微分した項の総和が、
log(x)等の複雑なxの関数が消えた、
(1/x)sin(x)
だけ、
になる関数が無い。
そのため、
(1/x)sin(x)
は不定積分が初等関数で表わせません。
また、
x/sin(x)
も不定積分が初等関数で表わせません。
その理由は、(1/sin(x))がxに掛かった初等関数が、それを微分した結果のいくつかの項の1つ(xを残した項)が、
x/sin(x)
にできる関数はありますが、その関数は
xlog(tan(x/2))
という、x掛ける(三角関数の対数関数)といった複雑な関数です。
その関数を微分した結果の、x/sin(x)の項以外の、xを微分して消した項は、
log(tan(x/2))
という複雑な関数になってしまいます。
その関数の不定積分は初等関数では表わせず、すなわち、別の初等関数を微分してlog(tan(x/2))にすることができない。
そのため、この複雑な関数は別の初等関数の微分によっては打ち消す事ができません。
結局、(xの関数)掛ける(三角関数の関数)という初等関数の多数の項の総和で表したどんな関数でも、
その関数の微分結果の各項にlog(tan(x/2))等の複雑な関数が出ても、各項同士でそれらが打ち消し合って消えて、
x/sin(x)
だけ、
になるというような関数が無い。
そのため、
x/sin(x)
は不定積分が初等関数で表わせません。
ましてや、
1/{(x)sin(x)}
といった、
1/sin(x)という三角関数の有理関数の項に、(1/x)といった、その関数(1/x)を微分して定数にすることもできない関数を掛け算した関数は、
(xの関数)掛ける(三角関数の関数)という初等関数の多数の項の総和でどんな関数を作っても、
その関数の各項の微分結果にlog(x)等のxの関数と三角関数の積や、log(tan(x/2))等の三角関数の複雑な関数とxの関数の積が出る。それらの複雑な関数が一時的なもので各項同士で打ち消し合って消えるということは無い。
そのため、そのような多数の項の関数を微分しても、
1/{(x)sin(x)}
だけ、
になる関数が無いと考えます。
そのため、
1/{(x)sin(x)}
は不定積分が初等関数では表せないと考えます。
ただし、この事例の様な、関係する原始関数を全部網羅して不定積分が初等関数で表せない事を判定する方法は、関係する原始関数が少ない場合にのみ有効な方法です。
「かろうじて初等関数で表される積分」
に記載した形の被積分関数の積分を判定するのには向いていないので、注意が必要です。
(事例3)
以下の関数を微分して得た各項は、他の関数の微分を組み合わせることでは作れないので、単独の各項の不定積分は初等関数で表せない。
(事例4)
以下の関数を微分して得た各項も、他の関数の微分を組み合わせることでは作れないので、単独の各項の不定積分は初等関数で表せない。
以上の事例のように、被積分関数が複雑化すれば、その複雑な被積分関数を含む式が微分で得られる原始関数の数が少なくなる。
そのため、その原始関数を全て組み合わせても、微分すると被積分関数が単独で得られる原始関数が無い可能性が高くなる。すなわち、不定積分が初等関数で表されない可能性が高くなる。
リンク:
高校数学の目次
『楕圓函數論』竹内 端三 著の現代仮名遣い版

ラインセグメント日記2017年11月21日『楕円函数論』の現代語訳
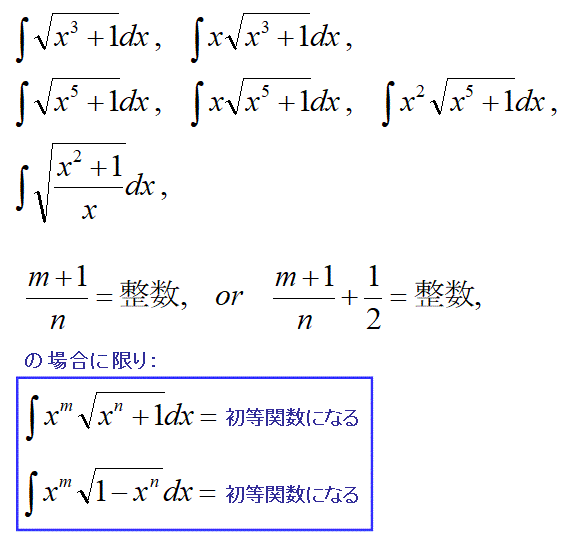












0 件のコメント:
コメントを投稿