垂直二等分線の方程式

佐藤の数学教科書「図形と方程式」編の勉強

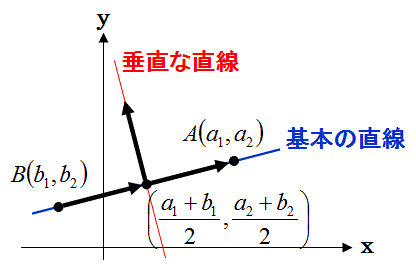
以下で、点Ａ（ａ_１，ａ_２）と点Ｂ（ｂ_１，ｂ_２）を結ぶ線分ＡＢの垂直二等分線の方程式を導く方法を説明します。

（点あるいはベクトルの座標値を記号であらわすときは、上図の様に添え字を付けて座標記号をあらわし、点の名前ＡとＢを引き継いだ記号であらわしてください。そうした方が、記号の意味の見通しが良くなるからです） 
 
（予備知識）
複雑な直線の方程式は、単純な形の基本的な直線の方程式に置きかえて考えます。
（難しい形の式は、全て、単純な形の式に置き換えて考えるのが数学のコツです。）

（まず、問題を単純化する）
上の概念図の座標軸（ｘ，ｙ）を、平行移動して、線分ＡＢの中点（その点を垂直二等分線が通る）を座標原点とする座標（Ｘ，Ｙ）で考える。

ここで、単純化した問題の解答を得た後で、解答を元の問題の解答へ翻訳できるように、元の問題との対応関係を与える式を、以下のように書いて記録しておく。

この座標系Ｘ，Ｙでは、上図のように、点Ａと点Ｂが原点に対して対称な位置にあります。点ＡのＸ座標＝Ａ_１とし、Ｙ座標＝Ａ_２と書き直して単純化する。

ここで、単純化した問題の解答を得た後で、解答を元の問題の解答へ翻訳できるように、元の問題との対応関係を与える式を、以下のように書いて記録しておく。

です。

（単純化した問題を解く）
上の図を見ると、点Ａと原点を通る直線の式は、

であらわせることがわかる。そして、
この直線に垂直で原点を通る直線の式は、

 （以上で、単純化した問題の解答が得られた）

（単純化した問題の解答を元の問題の解答へ翻訳する）
式５のＡ_１とＡ_２を、式３と４を使って、ａ_１、ａ_２、ｂ_１、ｂ_２に置き換える。

上の式のＸとＹを、式１と２を使って、ｘ、ｙに置き換える。

（解答おわり）

【第２の解答】
この答えは、以下の様に、垂直なベクトルの内積が０になる公式（式６）から速やかに導き出される。

（第２の解答おわり）

リンク：
高校数学の目次