佐藤の数学教科書「図形と方程式」編の勉強
【問1】
座標原点を中心にする半径1の円(x2+y2=1)に対して、点A( a1,a2)から引いた2つの接線の円との接点BとCの座標をもとめよ。
上の図で線分OAの長さをaとする。
(予備知識)
受験問題のときは、円と直線の方程式の問題は、図形の方程式をベクトルの式であらわして、図形で考えます。方程式を解いて計算するのは、計算の見通しがあまり良くありません。それに対して、ベクトルを利用した図形の問題を考えることは、計算の見通しを良くするからです。
しかし、どうしても方程式を使って解くように求められた場合は、以下のようにして解きます。
【解答1】先ず、座標軸を回転しない方法で解く。
円の式は、
x2+y2=1 (式1)
また、OAの長さaについて以下の式2が成り立つ。
(1)
円の接線の式を作る。
接点Bの座標をB( b1,b2)とし、接点Cの座標をC( c1,c2)する。
接点Bを通る円の接線の式は、接線の公式を使って、
とあらわされる。
この接線が点Aを通るため、以下の式がなりたつ。
(2)
接点Bの座標を円の式(式1)に代入する。
(3)
式4と式5を連立して接点B( b1,b2)の座標を求める。
-----(注意)------
ここで、式4と式5を連立した式は、以下の式4’と式1を連立して接点Bの(x,y)座標を求める式である。

x2+y2=1 (1)
この連立方程式は、接点Bと一緒に接点Cの座標を求める式であるとも言える。そのため、式4’は、接点BとCとを通る直線の式(極線)をあらわしている。
-----注意おわり--------
先ず、式4から、
式6を式5に代入して未知数b2を消去する。
その代入をしやすくするために、式5にa22を掛け算する。
これに式6を代入する。
未知数b1に関して、上の式を整理する。
この式を未知数b1に関して平方完成する。
(4)
この式を式6に代入して未知数b2を計算する。
この解は、接点Bと接点Cとの両方の解をあらわしている。
よって、接点BとCの座標(x,y)は、以下の式であらわせます。
接点Bは、
接点Cは、
(解答おわり)
【解答2】座標軸を回転して解く
ここで、円の式の次元をそろえるためにr=1という定数rを使う。
すると、円の式は以下の式1になる。
x2+y2=r2 (式1)
また、OAの長さaについて以下の式2が成り立つ。
(1)以下の図のように、XY座標軸を回転変換したst座標系を考える。
このst座標系への回転変換の式を単純化した。
その副作用で、XY座標系は、回転変換される上に、更に、拡大縮小変換もされる。
この場合に、以下の逆変換の式が成り立つ。
こうして回転変換したst座標系でグラフを観察すると、XY座標系で観察した円と直線のグラフは以下のグラフに変わる。
(確認した注意点)
座標を回転変換及び拡大縮小変換するだけならば、グラフ同士が接する関係は、変換の結果でも維持される。
そのため、変換されたst座標系で接点の座標を求め、その座標をXY座標系に逆変換すれば良い。
次に、上図のように、図から、接点の(s,t)座標を求める。
(方程式を解いて接点を計算するよりも、図形の考察により接点の座標を求める方が、計算の見通しが良いので優れた解き方である。)
得られた(s,t)座標を、以下の様にして(x,y)座標に逆変換する。
そして、最後にr=1として、式を仕上げる。
以上で得た(x,y)座標が接点の座標である。
(最後にr=1を代入する前までの式では、rを含む各定数が長さの次元を持つと考え、xとyを与える式の各項の次元が長さの次元にそろっていることを確認する検算ができた)
(解答おわり)
(補足)
座標の回転変換を利用して解くと、計算がずいぶん楽になった。
リンク:
高校数学の目次
【問1】
座標原点を中心にする半径1の円(x2+y2=1)に対して、点A( a1,a2)から引いた2つの接線の円との接点BとCの座標をもとめよ。
上の図で線分OAの長さをaとする。
(予備知識)
受験問題のときは、円と直線の方程式の問題は、図形の方程式をベクトルの式であらわして、図形で考えます。方程式を解いて計算するのは、計算の見通しがあまり良くありません。それに対して、ベクトルを利用した図形の問題を考えることは、計算の見通しを良くするからです。
しかし、どうしても方程式を使って解くように求められた場合は、以下のようにして解きます。
【解答1】先ず、座標軸を回転しない方法で解く。
円の式は、
x2+y2=1 (式1)
また、OAの長さaについて以下の式2が成り立つ。
(1)
円の接線の式を作る。
接点Bの座標をB( b1,b2)とし、接点Cの座標をC( c1,c2)する。
接点Bを通る円の接線の式は、接線の公式を使って、
とあらわされる。
この接線が点Aを通るため、以下の式がなりたつ。
(2)
接点Bの座標を円の式(式1)に代入する。
(3)
式4と式5を連立して接点B( b1,b2)の座標を求める。
-----(注意)------
ここで、式4と式5を連立した式は、以下の式4’と式1を連立して接点Bの(x,y)座標を求める式である。

x2+y2=1 (1)
この連立方程式は、接点Bと一緒に接点Cの座標を求める式であるとも言える。そのため、式4’は、接点BとCとを通る直線の式(極線)をあらわしている。
-----注意おわり--------
先ず、式4から、
式6を式5に代入して未知数b2を消去する。
その代入をしやすくするために、式5にa22を掛け算する。
これに式6を代入する。
未知数b1に関して、上の式を整理する。
この式を未知数b1に関して平方完成する。
(4)
この式を式6に代入して未知数b2を計算する。
この解は、接点Bと接点Cとの両方の解をあらわしている。
よって、接点BとCの座標(x,y)は、以下の式であらわせます。
接点Bは、
接点Cは、
(解答おわり)
【解答2】座標軸を回転して解く
ここで、円の式の次元をそろえるためにr=1という定数rを使う。
すると、円の式は以下の式1になる。
x2+y2=r2 (式1)
また、OAの長さaについて以下の式2が成り立つ。
(1)以下の図のように、XY座標軸を回転変換したst座標系を考える。
このst座標系への回転変換の式を単純化した。
その副作用で、XY座標系は、回転変換される上に、更に、拡大縮小変換もされる。
この場合に、以下の逆変換の式が成り立つ。
こうして回転変換したst座標系でグラフを観察すると、XY座標系で観察した円と直線のグラフは以下のグラフに変わる。
(確認した注意点)
座標を回転変換及び拡大縮小変換するだけならば、グラフ同士が接する関係は、変換の結果でも維持される。
そのため、変換されたst座標系で接点の座標を求め、その座標をXY座標系に逆変換すれば良い。
次に、上図のように、図から、接点の(s,t)座標を求める。
(方程式を解いて接点を計算するよりも、図形の考察により接点の座標を求める方が、計算の見通しが良いので優れた解き方である。)
得られた(s,t)座標を、以下の様にして(x,y)座標に逆変換する。
そして、最後にr=1として、式を仕上げる。
以上で得た(x,y)座標が接点の座標である。
(最後にr=1を代入する前までの式では、rを含む各定数が長さの次元を持つと考え、xとyを与える式の各項の次元が長さの次元にそろっていることを確認する検算ができた)
(解答おわり)
(補足)
座標の回転変換を利用して解くと、計算がずいぶん楽になった。
リンク:
高校数学の目次








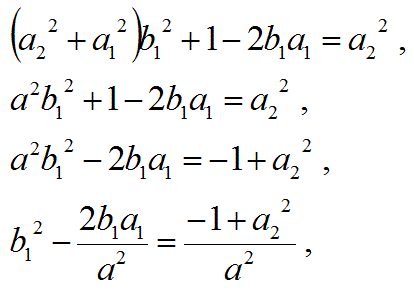



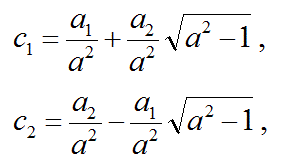




0 件のコメント:
コメントを投稿