

「微分・積分」の勉強
なめらかな曲線の接線は、微分によって初めて正しく定義できる。
接線を求める式に重根が含まれるとは限らない。
【問1】hの値を変えたとき、
放物線 y=x2+h (式1)
と、円 x2+(y-1)2=1 (式2)
とが接する場合に、その接点(x,y)の値を求めよ。
《以下で、この問題の4つの解答を示す》
【解答1】微分を使って解く解答
【解答2】微分を使わないで、方程式の変形のみで解く面倒くさい解答(重解の、特殊な判別式を使う)
【解答3】グラフの図形を使って簡単に解く解答(重解の判別式の意味を考える)
【解答4】方程式群を等価な方程式群に変換して解く解答
(解答1の解答の方針)
なめらかな曲線の接線は、微分によって初めて正しく定義できるので、微分により接線の式を計算して方程式を書く。
【解答1】
(1)
接点(x,y)において、
式1から、
放物線 y=x2+h (式1’)
式2から、
円 x2+(y-1)2=1 (式2’)
(2)
式1の放物線の接点(x,y)における接線の傾きy’は、式1の関数をxで微分して計算し、
y’=2x (式3)
である。
(3)
式2の円の接点(x,y)における接線の傾きy’は、
法線の傾き(y-1)/xの逆数に(-1)を掛け算したものであって、
y’=-x/(y-1) (式4)
である。
(4)
この2つの接線の傾きの値が等しいので、
式3=式4:
この式5を解くと、
x=0 (式6)
or
y-1=-1/2
y=1/2 (式7)
(5)
(式6の場合の接点を求める)
式6を式2に代入する。
(y-1)2=1
(y-1)=±1
y=2
or
y=0
接点は、
(x,y)=(0,0) (式8)
or
(x,y)=(0,2) (式9)
(5-1)
式8の場合に、式8を式1に代入する。
h=0
(5-2)
式9の場合に、式9を式1に代入する。
h=2
(5-3)
よって
接点=(0,0)でh=0
or
接点=(0,2)でh=2
(以上が、第1の種類の接点)
(6)
(式7の場合の接点を求める)
式7(y=1/2)を式4に代入する。
式1より
接点は、
このとき、
(以上が第2の種類の接点)
(解答1おわり)
【解答2】
この問題を微分を使わないで、図形の交点が接点となる場合に重解になる事を利用して解く場合は、以下のように面倒くさい解き方になります。
この方程式で、以下の式3の置き換えをして解く。
この式4から、以下の式5と式6を得て、式6からxの式を得る。
この解を、以下の様にグラフで表す。
hを変えた場合の解の様子を、以下のグラフで考える。
この様に、hが大きくなると、4つの交点のうちの2つが消える事を認識する。
この事をふまえて考察すると、2つのグラフが接することになる条件は、以下の3つである。
これら、各場合を、以下の様にして解く。
この式は、重解となる条件をあらわすので、重解の判別式であると解釈できる。
この判別式は、等価な以下の連立方程式8-1と8-1bに変形できる。
これが、場合2の解である。
これが、場合3の解である。
(解答2おわり)
【解答3】
以下のように、図で考えて図から答えを得て計算すると簡単に解ける。

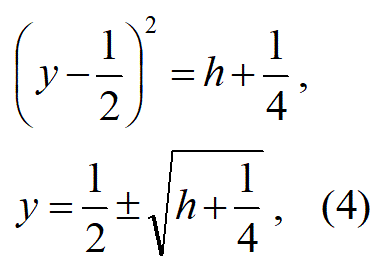
式(1)と式(2)は、この式(4)と式(2)の連立方程式に変換された。((注意)yだけで表される式(4)だけでは、どのようにしても、x軸に平行な傾きで曲線が接する接点を求めることはできない。元の式(1)と式(2)のグラフを、y軸を基準にして見ると、y軸を基準にして傾きが無限大になる接線(x軸に平行な直線)は、yの関数として表すことができない。それが、yだけの式(4)からx軸に平行な傾きの曲線の接点が求められない原因である)。
式(4)と式(2)の関係を、以下の図であらわす。

hを変えた場合の解の様子を、以下のグラフで考える。
この様に、hが大きくなると、4つの交点のうちの2つが消える事を認識する。
この事をふまえて、式4と式2の関係を考察する。
式1と式2の2つのグラフが接することになる条件は、式4と式2の2つのグラフの4つの交点のうちの2つが重なって重解になる条件と同じである。
各場合の、重解になる条件をあらわす式が、その各場合の重解の判別式である。
重解になる条件は、以下の3つの場合がある。
これら、各場合を、以下の様にして解く。
これが、場合1の解である。
これが、場合2の解である。

これが、場合3の解である。
(解答3おわり)
【解答4】
以下の様に、方程式群を等価な方程式群に変換した上で、その方程式群で、図形の交点が接点となる場合に重解になる事に基づき、接点を求めることができます。
式1を以下の式3に変形した上で式2に代入して式4を求める。
この式4と式2を連立した式は、元の式1と式2を連立した式に等価な式である。
この式2と式4の1組の式を連立して得た共有点(x,y)の解が、hの値に応じて2重に得られる共有点の解が、式1と式2のグラフの接点の解になる。

式4のグラフは上図の、X軸に平行な2本の直線である。式2のグラフは上図の、赤線で表した円のグラフである。上図の青線で表したグラフは、式1の表すグラフである。
-------(視点を変えた式の解釈のはじめ)---------
元の式1と式2に等価な式2と式4では、共有点(x,y)が同じになるという共通点はあるが、1つ、大きな違いを持っている。
先ず、式2のグラフ(円のグラフ)と式4のグラフ(X軸に平行な2つの直線のうちの1本の(X軸に平行な)直線)とが接する場合は、その接点は、式1のグラフと式2のグラフの接点でもある。
しかし、次に、式4の表す2つの直線が1本の直線になる条件(式4が重解を持つ条件)では、式4の表す2本の直線が1本の直線に収束する。その場合には、その(X軸に平行な)1本の直線と、式2のグラフ(円のグラフ)とには2つの交点がある。そのうちの1つの交点は、式2のグラフ(円のグラフ)と式4のグラフとの接点では無いが、式1のグラフと式2のグラフ(円のグラフ)の接点である。
そのように、式1と式2に等価なこの式(式2と式4)は、元の式(式1と式2)の接点という性質を完全に受け継ぐ式では無いという違いがある。
-------(視点を変えた式の解釈おわり)--------
その共有点(x,y)の解が2重に得られる場合には、以下の2つの場合があります。
(場合A)x軸に平行な2本の直線と円のグラフとの4つの交点(x,y)のうちの2つの交点が、1つのyの値に対して2つのxの値の解のxの値の重解に収束する場合。
(場合B)接線の方向ベクトルがY軸に射影され得る接線とグラフとの接点は、式(4)がyの重解を持つことで発見できる。ただし、そのyの値について、式(2)でxの実数値が求められる必要がある。

場合Bでは、上図のように考える。
接線がグラフに接することで、接線とグラフの共有点が1つ(重解)になる接点では、以下の事が起きている。
その接線を微小量Δtの幅で平行移動した直線とグラフの共有点については、接線の方向で隔たった2点になる。
その2点がY座標で区別できるためには、接線の方向ベクトルがY軸に射影される成分を持たなければならない。接線の方向ベクトルは、接線上のどの点でもYの値が一定になってしまうことになるX軸に平行な方向を向いていてはならない。
X軸に平行な接線とグラフとの接点では場合Bの変数yを用いては接点の重解が判別できない。そのため、変数yの式(4)ではその接点では変数Yの値の重解を持たない。
X軸に平行な接線とグラフの接点を調べるためには、場合Aで、その接線の方向ベクトルが射影され得るX軸の変数xを用いて調べる必要がある。
以下で、この2つの場合の接点の解を求める。
(場合A)x軸に平行な直線とグラフの2つの交点(x,y)のx座標を求める方程式が重解を持つ場合。
すなわち、式(4)で与えられる一定のyの値を定数と考えた変数xの方程式(2)の解を求める。それにより、x軸に平行な直線と式(2)のグラフの2つの交点の変数xの値が重解になる場合を調べる事で接点を求める。
その2つの交点が重解になる場合に、式6のxの解が重解(x=0)になる。重解になる場合の変数yの値は式(4)で与えられる。その場合は、以下の2つのyの値の接線と式(2)のグラフが接する場合である。
(場合B)接線の方向ベクトルがY軸に射影され得る方向を向く場合は、式(4)がyの重解を持つことで接点が発見できる。ただし、そのyの値について、式(2)を解いてxの実数解が求められる必要がある。
すなわち、xの値が式12の2つの場合には、式10のyの解が重解になる。
---(注意)-----------
この式11を求めて、それを式2に代入してxの値を求める場合に、
「円と放物線が接する場合」の問題の場合には、
式2を満足するxの実数解が無い。
その場合には、場合Bの接点が存在しない。
----注意おわり-------
以上をまとめると、
接点の解は、場合Aの、式6のX=0と、式7と式8の場合と、
場合Bの、式11と式12の場合である。
(解答4おわり)
(補足1)
解答4において、場合Aと場合Bとの2つの場合で重解を求める必要性があるのは、以下の理由からです。
場合Bの重解を求めるため式4を使ってyの重解を得ることで接点が発見できる場合は、接線の方向ベクトルがY軸に射影され得る場合に限られる。
接線とグラフの1つの接点がある場合に、下図のように接線を平行移動した直線とグラフの交点を求めると、接線上の異なる2点に分かれた交点が求められる。その分かれた2点のy座標の値が異なるのでなければ変数yの式を使っては接点の重解が判別できない。そのため、変数yの式4では、X軸に平行な接線(Y座標値が一定値なグラフ)との接点に関わるyの重解を持たない。
場合Bでは、上図のように考える。
接線がグラフに接することで、接線とグラフの共有点が1つ(重解)になる接点では、以下の事が起きている。
接線で点の解が重解を持ち、接線に平行な直線とグラフとが共有する2つの共有点は接線の方向で隔たっている。そのため、共有点が2つある事を見分けるためには、接線の方向のベクトルが変数yのY座標軸の方向に0以外の値の成分を持つ必要がある。
接線の方向のベクトルがy座標値が一定になるようにX軸に平行な場合は、変数Yの式によっては共有点が2つある事が見分けられず、隔たった2つの共有点のY座標は1つのみになる。
そのため、隔たった2つの共有点が1つになって重解になるという接点の特徴を観察して接点を判別するためには、接線の方向は、X軸に平行であってはならない。
場合Aについては、以下の様に考える。
放物線を部分部分に分解すると、各部分は直線に近似できる。
放物線と円の接点を求める問題は、その直線と円との接点を考える問題と解釈できる。
放物線のグラフの部分を表す直線の、x座標を変数yの関数としてグラフを表そうとする場合、
その直線の式は、
x=ay+b
という関数でしか扱えない。

y=-1, という直線の式は、下の図のように、x=f(y)と表すyの関数で表すことができない。
y=-1は、yの関数ではない。

x=ay+bというyの関数によっては、x軸に平行な放物線の部分に近似させた直線を表すことができない。
そのため、x軸に平行な放物線の部分の直線は、yの関数を使っては、決して表す事ができない。
yの関数で、放物線のその部分が表せないので、その部分での接点もyの関数を使っては求める事ができない。
そのような事情があるので、X軸に平行な接線とグラフの接点は、変数yによっては、接点が判別できない。そのため、変数yの式4はX軸に平行な接線との接点に関しては、変数yの重解を持つことも無い。
x軸に平行な接線とグラフの接点についての場合Aでは、その接線の方向ベクトルが射影し得るX軸の変数xを使って判別する。方程式2でyの値を固定して定数とした場合の変数xの解を求めて、方程式2がxの重解を持つ事を発見することで接点を発見する必要がある。
(補足2)
解答2においては、解答2の式4によって求めた4つの共有点を使って接点を求めた。解答2でも接線にグラフが接する事で重解になる接点は、その接線の方向ベクトルがX軸に射影し得る場合にのみ、接点が発見できる。接線の方向ベクトルがY軸に平行である場合は接点が発見できない。
上図のように、接点は、その接線が、微小量Δtの幅で平行移動した場合に接線の方向で距離を隔てた2点でグラフと交わる。変数xによって接点が判別できる接線の方向はY軸の方向に平行であってはならない。
Y軸に平行な接線とグラフの接点については、解答4と同様に、解答2の式4のx座標の重解によっては求める事ができません。
しかし、放物線の接線がY軸に平行になる事は無いため、
解答2では、Y軸に平行な接線とグラフの接点を求める必要性が無かった。そのため、問題が生じなかったのです。
(微分との関係)
グラフy=f(x)の接線との接点を、変数xの重解によって判別する際に、Y軸に平行な接線との接点については判別できない(重解が無い)事は、微分によって接点を求める方法では、以下の事と対応しています。
なめらかな曲線の接線は、微分によって初めて正しく定義できる。
接線を求める式に重根が含まれるとは限らない。
【問1】hの値を変えたとき、
放物線 y=x2+h (式1)
と、円 x2+(y-1)2=1 (式2)
とが接する場合に、その接点(x,y)の値を求めよ。
《以下で、この問題の4つの解答を示す》
【解答1】微分を使って解く解答
【解答2】微分を使わないで、方程式の変形のみで解く面倒くさい解答(重解の、特殊な判別式を使う)
【解答3】グラフの図形を使って簡単に解く解答(重解の判別式の意味を考える)
【解答4】方程式群を等価な方程式群に変換して解く解答
(解答1の解答の方針)
なめらかな曲線の接線は、微分によって初めて正しく定義できるので、微分により接線の式を計算して方程式を書く。
【解答1】
(1)
接点(x,y)において、
式1から、
放物線 y=x2+h (式1’)
式2から、
円 x2+(y-1)2=1 (式2’)
(2)
式1の放物線の接点(x,y)における接線の傾きy’は、式1の関数をxで微分して計算し、
y’=2x (式3)
である。
(3)
式2の円の接点(x,y)における接線の傾きy’は、
法線の傾き(y-1)/xの逆数に(-1)を掛け算したものであって、
y’=-x/(y-1) (式4)
である。
(4)
この2つの接線の傾きの値が等しいので、
式3=式4:
この式5を解くと、
x=0 (式6)
or
y-1=-1/2
y=1/2 (式7)
(5)
(式6の場合の接点を求める)
式6を式2に代入する。
(y-1)2=1
(y-1)=±1
y=2
or
y=0
接点は、
(x,y)=(0,0) (式8)
or
(x,y)=(0,2) (式9)
(5-1)
式8の場合に、式8を式1に代入する。
h=0
(5-2)
式9の場合に、式9を式1に代入する。
h=2
(5-3)
よって
接点=(0,0)でh=0
or
接点=(0,2)でh=2
(以上が、第1の種類の接点)
(6)
(式7の場合の接点を求める)
式7(y=1/2)を式4に代入する。
式1より
接点は、
このとき、
(以上が第2の種類の接点)
(解答1おわり)
【解答2】
この問題を微分を使わないで、図形の交点が接点となる場合に重解になる事を利用して解く場合は、以下のように面倒くさい解き方になります。
この方程式で、以下の式3の置き換えをして解く。
この式4から、以下の式5と式6を得て、式6からxの式を得る。
この解を、以下の様にグラフで表す。
hを変えた場合の解の様子を、以下のグラフで考える。
この様に、hが大きくなると、4つの交点のうちの2つが消える事を認識する。
この事をふまえて考察すると、2つのグラフが接することになる条件は、以下の3つである。
これら、各場合を、以下の様にして解く。
この式は、重解となる条件をあらわすので、重解の判別式であると解釈できる。
この判別式は、等価な以下の連立方程式8-1と8-1bに変形できる。
式8-1bを以下の式に変形する。
これが、場合1の解である。これが、場合2の解である。
これが、場合3の解である。
(解答2おわり)
【解答3】
以下のように、図で考えて図から答えを得て計算すると簡単に解ける。

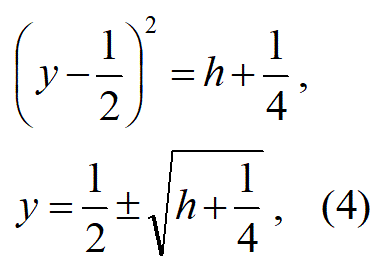
式(1)と式(2)は、この式(4)と式(2)の連立方程式に変換された。((注意)yだけで表される式(4)だけでは、どのようにしても、x軸に平行な傾きで曲線が接する接点を求めることはできない。元の式(1)と式(2)のグラフを、y軸を基準にして見ると、y軸を基準にして傾きが無限大になる接線(x軸に平行な直線)は、yの関数として表すことができない。それが、yだけの式(4)からx軸に平行な傾きの曲線の接点が求められない原因である)。
式(4)と式(2)の関係を、以下の図であらわす。

hを変えた場合の解の様子を、以下のグラフで考える。
この様に、hが大きくなると、4つの交点のうちの2つが消える事を認識する。
この事をふまえて、式4と式2の関係を考察する。
式1と式2の2つのグラフが接することになる条件は、式4と式2の2つのグラフの4つの交点のうちの2つが重なって重解になる条件と同じである。
各場合の、重解になる条件をあらわす式が、その各場合の重解の判別式である。
重解になる条件は、以下の3つの場合がある。
これら、各場合を、以下の様にして解く。
これが、場合1の解である。
これが、場合2の解である。

これが、場合3の解である。
(解答3おわり)
【解答4】
以下の様に、方程式群を等価な方程式群に変換した上で、その方程式群で、図形の交点が接点となる場合に重解になる事に基づき、接点を求めることができます。
式1を以下の式3に変形した上で式2に代入して式4を求める。
この式4と式2を連立した式は、元の式1と式2を連立した式に等価な式である。
この式2と式4の1組の式を連立して得た共有点(x,y)の解が、hの値に応じて2重に得られる共有点の解が、式1と式2のグラフの接点の解になる。

式4のグラフは上図の、X軸に平行な2本の直線である。式2のグラフは上図の、赤線で表した円のグラフである。上図の青線で表したグラフは、式1の表すグラフである。
-------(視点を変えた式の解釈のはじめ)---------
元の式1と式2に等価な式2と式4では、共有点(x,y)が同じになるという共通点はあるが、1つ、大きな違いを持っている。
先ず、式2のグラフ(円のグラフ)と式4のグラフ(X軸に平行な2つの直線のうちの1本の(X軸に平行な)直線)とが接する場合は、その接点は、式1のグラフと式2のグラフの接点でもある。
しかし、次に、式4の表す2つの直線が1本の直線になる条件(式4が重解を持つ条件)では、式4の表す2本の直線が1本の直線に収束する。その場合には、その(X軸に平行な)1本の直線と、式2のグラフ(円のグラフ)とには2つの交点がある。そのうちの1つの交点は、式2のグラフ(円のグラフ)と式4のグラフとの接点では無いが、式1のグラフと式2のグラフ(円のグラフ)の接点である。
そのように、式1と式2に等価なこの式(式2と式4)は、元の式(式1と式2)の接点という性質を完全に受け継ぐ式では無いという違いがある。
-------(視点を変えた式の解釈おわり)--------
その共有点(x,y)の解が2重に得られる場合には、以下の2つの場合があります。
(場合A)x軸に平行な2本の直線と円のグラフとの4つの交点(x,y)のうちの2つの交点が、1つのyの値に対して2つのxの値の解のxの値の重解に収束する場合。
(場合B)接線の方向ベクトルがY軸に射影され得る接線とグラフとの接点は、式(4)がyの重解を持つことで発見できる。ただし、そのyの値について、式(2)でxの実数値が求められる必要がある。

場合Bでは、上図のように考える。
接線がグラフに接することで、接線とグラフの共有点が1つ(重解)になる接点では、以下の事が起きている。
その接線を微小量Δtの幅で平行移動した直線とグラフの共有点については、接線の方向で隔たった2点になる。
その2点がY座標で区別できるためには、接線の方向ベクトルがY軸に射影される成分を持たなければならない。接線の方向ベクトルは、接線上のどの点でもYの値が一定になってしまうことになるX軸に平行な方向を向いていてはならない。
X軸に平行な接線とグラフとの接点では場合Bの変数yを用いては接点の重解が判別できない。そのため、変数yの式(4)ではその接点では変数Yの値の重解を持たない。
X軸に平行な接線とグラフの接点を調べるためには、場合Aで、その接線の方向ベクトルが射影され得るX軸の変数xを用いて調べる必要がある。
以下で、この2つの場合の接点の解を求める。
(場合A)x軸に平行な直線とグラフの2つの交点(x,y)のx座標を求める方程式が重解を持つ場合。
すなわち、式(4)で与えられる一定のyの値を定数と考えた変数xの方程式(2)の解を求める。それにより、x軸に平行な直線と式(2)のグラフの2つの交点の変数xの値が重解になる場合を調べる事で接点を求める。
その2つの交点が重解になる場合に、式6のxの解が重解(x=0)になる。重解になる場合の変数yの値は式(4)で与えられる。その場合は、以下の2つのyの値の接線と式(2)のグラフが接する場合である。
(場合B)接線の方向ベクトルがY軸に射影され得る方向を向く場合は、式(4)がyの重解を持つことで接点が発見できる。ただし、そのyの値について、式(2)を解いてxの実数解が求められる必要がある。
すなわち、xの値が式12の2つの場合には、式10のyの解が重解になる。
---(注意)-----------
この式11を求めて、それを式2に代入してxの値を求める場合に、
「円と放物線が接する場合」の問題の場合には、
式2を満足するxの実数解が無い。
その場合には、場合Bの接点が存在しない。
----注意おわり-------
以上をまとめると、
接点の解は、場合Aの、式6のX=0と、式7と式8の場合と、
場合Bの、式11と式12の場合である。
(解答4おわり)
(補足1)
解答4において、場合Aと場合Bとの2つの場合で重解を求める必要性があるのは、以下の理由からです。
場合Bの重解を求めるため式4を使ってyの重解を得ることで接点が発見できる場合は、接線の方向ベクトルがY軸に射影され得る場合に限られる。
接線とグラフの1つの接点がある場合に、下図のように接線を平行移動した直線とグラフの交点を求めると、接線上の異なる2点に分かれた交点が求められる。その分かれた2点のy座標の値が異なるのでなければ変数yの式を使っては接点の重解が判別できない。そのため、変数yの式4では、X軸に平行な接線(Y座標値が一定値なグラフ)との接点に関わるyの重解を持たない。
場合Bでは、上図のように考える。
接線がグラフに接することで、接線とグラフの共有点が1つ(重解)になる接点では、以下の事が起きている。
接線で点の解が重解を持ち、接線に平行な直線とグラフとが共有する2つの共有点は接線の方向で隔たっている。そのため、共有点が2つある事を見分けるためには、接線の方向のベクトルが変数yのY座標軸の方向に0以外の値の成分を持つ必要がある。
接線の方向のベクトルがy座標値が一定になるようにX軸に平行な場合は、変数Yの式によっては共有点が2つある事が見分けられず、隔たった2つの共有点のY座標は1つのみになる。
そのため、隔たった2つの共有点が1つになって重解になるという接点の特徴を観察して接点を判別するためには、接線の方向は、X軸に平行であってはならない。
場合Aについては、以下の様に考える。
放物線を部分部分に分解すると、各部分は直線に近似できる。
放物線と円の接点を求める問題は、その直線と円との接点を考える問題と解釈できる。
放物線のグラフの部分を表す直線の、x座標を変数yの関数としてグラフを表そうとする場合、
その直線の式は、
x=ay+b
という関数でしか扱えない。

y=-1, という直線の式は、下の図のように、x=f(y)と表すyの関数で表すことができない。
y=-1は、yの関数ではない。

x=ay+bというyの関数によっては、x軸に平行な放物線の部分に近似させた直線を表すことができない。
そのため、x軸に平行な放物線の部分の直線は、yの関数を使っては、決して表す事ができない。
yの関数で、放物線のその部分が表せないので、その部分での接点もyの関数を使っては求める事ができない。
そのような事情があるので、X軸に平行な接線とグラフの接点は、変数yによっては、接点が判別できない。そのため、変数yの式4はX軸に平行な接線との接点に関しては、変数yの重解を持つことも無い。
x軸に平行な接線とグラフの接点についての場合Aでは、その接線の方向ベクトルが射影し得るX軸の変数xを使って判別する。方程式2でyの値を固定して定数とした場合の変数xの解を求めて、方程式2がxの重解を持つ事を発見することで接点を発見する必要がある。
(補足2)
解答2においては、解答2の式4によって求めた4つの共有点を使って接点を求めた。解答2でも接線にグラフが接する事で重解になる接点は、その接線の方向ベクトルがX軸に射影し得る場合にのみ、接点が発見できる。接線の方向ベクトルがY軸に平行である場合は接点が発見できない。
上図のように、接点は、その接線が、微小量Δtの幅で平行移動した場合に接線の方向で距離を隔てた2点でグラフと交わる。変数xによって接点が判別できる接線の方向はY軸の方向に平行であってはならない。
Y軸に平行な接線とグラフの接点については、解答4と同様に、解答2の式4のx座標の重解によっては求める事ができません。
しかし、放物線の接線がY軸に平行になる事は無いため、
解答2では、Y軸に平行な接線とグラフの接点を求める必要性が無かった。そのため、問題が生じなかったのです。
(微分との関係)
グラフy=f(x)の接線との接点を、変数xの重解によって判別する際に、Y軸に平行な接線との接点については判別できない(重解が無い)事は、微分によって接点を求める方法では、以下の事と対応しています。
変数xによるグラフy=f(x)の微分係数f'(x)を求めて接点を求める場合は、接点では、変数xによる関数の微分係数が同じになる事を利用します。

しかし、上図のように、y=f(x)のグラフのY軸に平行な部分には変数xによる微分係数f'(x)が存在しないので変数xでのグラフy=f(x)の調査では接点が発見できない。(変数yでグラフを表して、変数yでの微分係数を調べればY軸に平行な接線x=-1とグラフとの接点(-1,0)が発見できる)
リンク:
高校数学の目次






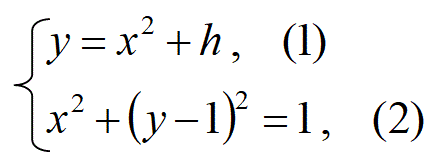








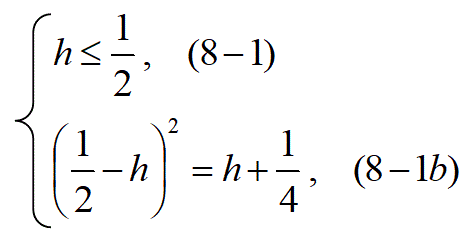


















0 件のコメント:
コメントを投稿