

ベクトルの外積が複素数の積で表わせる関係を初めて学ぶときは、
以下のように考えてこの関係があることを納得して学ぶ事が望ましいです。
【問1】
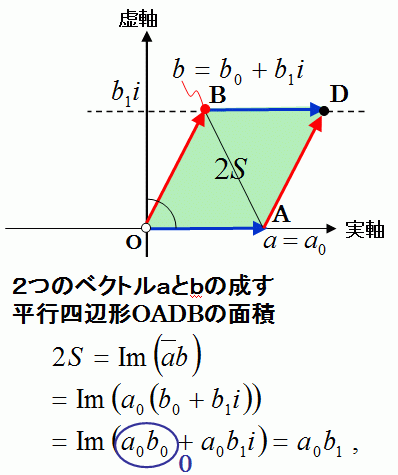
下図のような、複素数平面上のベクトルaとbで作られる平行四辺形(長方形)の面積2Sを計算せよ。
面積2Sは、上の式であらわせます。
【問2】
下図のような、左に90度回転したベクトルaとbで作られる平行四辺形(長方形)の面積2Sを計算せよ。
面積2Sは、上の式であらわせます。
【問3】
下図のような、複素数平面上のベクトルaと、実軸方向に平行に傾けたベクトルbで作られる平行四辺形(長方形)の面積2Sを計算せよ。
【問4】
下図のような、複素数平面上のベクトルbと、虚軸方向に平行に傾けたベクトルaで作られる平行四辺形(長方形)の面積2Sを計算せよ。
【問5】
下図のような、ベクトルaとbで作られる平行四辺形(長方形)の面積2Sを計算せよ。
この式は、個別に成分に分解した以下の式で計算することができます。
この計算は、以下の図形の面積の変形操作と解釈できます。
この面積の式は、以下の様に、まとまった複素数同士の積の計算の結果の一部であると解釈することができます。
この式の実数成分は、以下のようにベクトルの内積をあらわし、
虚数成分は、以下のようにベクトルの作る平行四辺形の面積をあらわします。
ここで、2つのベクトルの成す平行四辺形DBOAの面積をベクトルの掛け算(×)であらわし、ベクトルの外積と呼びます。
(注意)
ベクトルの外積の定義を厳密に言うと、
「2つのベクトルどちらにも垂直な方向(この図の場合は紙面に垂直な方向)のベクトルを計算すること。そのベクトルの長さは、平行四辺形DBOAの面積にする。」
です。
リンク:
第2講4節 点と直線の距離(三角形の面積)
追加講 三角形の面積と行列式
高校数学の目次










0 件のコメント:
コメントを投稿