【問1】
以下の微分方程式を解け。
【解答】
ラプラス変換を利用して以下の様に計算して解く。
式3から6を使って式1をラプラス変換する。
この式は、以下の形の式に分解できる。
この式8を逆ラプラス変換する。
(解答おわり)
(補足)
ラプラス変換は、 t 座標であらわした関数 f と s 座標であらわした関数 F の間の写像変換と考えることができる。
その写像は、 t 座標であらわした式の1つの項に、写像先の s 座標であらわした1つの項が対応する。
式の写像は項単位で行なう。写像の単位の項を写像し易いように、写像する式は単純な形の式の項の和に分割してから写像変換する。
特に、 t 座標の関数 f の微分演算が、 s 座標では、s を関数 F に掛け算した項ともう1つの項の和に変換される特徴がある。
写像変換した後で、s 座標での s の加減乗除で関数 F を計算する。その関数 F の式を t 座標であらわした関数 f に逆写像する。
そうすることで、t 座標での微分方程式の解 f を解くことができる。
リンク:
高校数学の目次
以下の微分方程式を解け。
【解答】
ラプラス変換を利用して以下の様に計算して解く。
式3から6を使って式1をラプラス変換する。
この式は、以下の形の式に分解できる。
(補足)
ラプラス変換は、 t 座標であらわした関数 f と s 座標であらわした関数 F の間の写像変換と考えることができる。
その写像は、 t 座標であらわした式の1つの項に、写像先の s 座標であらわした1つの項が対応する。
式の写像は項単位で行なう。写像の単位の項を写像し易いように、写像する式は単純な形の式の項の和に分割してから写像変換する。
特に、 t 座標の関数 f の微分演算が、 s 座標では、s を関数 F に掛け算した項ともう1つの項の和に変換される特徴がある。
写像変換した後で、s 座標での s の加減乗除で関数 F を計算する。その関数 F の式を t 座標であらわした関数 f に逆写像する。
そうすることで、t 座標での微分方程式の解 f を解くことができる。
リンク:
高校数学の目次
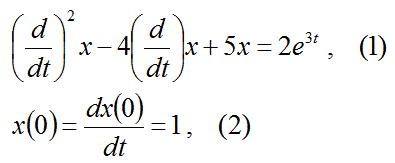

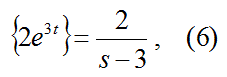

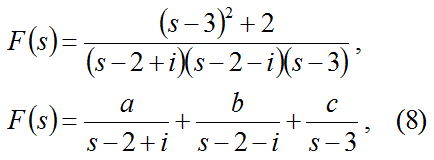


0 件のコメント:
コメントを投稿