

「微分・積分」の勉強
(1)積分:
以下の問題を考えます。
【問題】
なぜ、半径 r の球の体積Vは、
体積V=(4π/3) r3
なのか。
この問題は、以下の様に解くことができます。
先に、半径 r の球の表面積Sは、
表面積S=4π r2
であることを求めておきます。
次に、以下の図のように、球を玉ネギ状に、厚さΔrの皮の集合と考えます。
その1つの皮の体積を計算します。
皮の厚さをΔrとします。
球の皮の厚さΔrあたりの皮の体積ΔVが求められました。
ΔV=4π r2Δr
この皮の体積の総和が球の体積Vです。
V=4π((Δr)2Δr+(2Δr)2Δr+(3Δr)2Δr+・・・)
= 4π(Δr)3 (1+22+32+42・・・+n2)
= 4π(Δr)3 n(n+(1/2))(n+1)/3
=4π(nΔr)3 {1+(1/(2n))}{1+(1/n)}/3
=(4π r3/3){1+(1/(2n))}{1+(1/n)}
→ 4π r3/3
( r=n(Δr))
(この計算で用いた2乗の数列の和の式はここをクリックした先のページにあります
これから、半径 r の球の体積Vは、
体積V=(4π/3) r3
になることがわかりました。
この様に、要素に分割して総和を計算することが「積分」をするということです。
【別解】
以下の様に、直接に球の体積を求めることもできます。
先ず、半径1の球の体積を計算します。
これで、半径1の球の体積が計算できました。
これから、半径 r の球の体積Vは、
体積V=(4π/3) r3
になることがわかりました。
リンク:
球の体積・表面積の求め方!公式や覚え方、なぜそうなるかを徹底解説!
高校数学の目次
(1)積分:
以下の問題を考えます。
【問題】
なぜ、半径 r の球の体積Vは、
体積V=(4π/3) r3
なのか。
この問題は、以下の様に解くことができます。
先に、半径 r の球の表面積Sは、
表面積S=4π r2
であることを求めておきます。
次に、以下の図のように、球を玉ネギ状に、厚さΔrの皮の集合と考えます。
その1つの皮の体積を計算します。
皮の厚さをΔrとします。
ΔV=4π r2Δr
この皮の体積の総和が球の体積Vです。
V=4π((Δr)2Δr+(2Δr)2Δr+(3Δr)2Δr+・・・)
= 4π(Δr)3 (1+22+32+42・・・+n2)
= 4π(Δr)3 n(n+(1/2))(n+1)/3
=4π(nΔr)3 {1+(1/(2n))}{1+(1/n)}/3
=(4π r3/3){1+(1/(2n))}{1+(1/n)}
→ 4π r3/3
( r=n(Δr))
(この計算で用いた2乗の数列の和の式はここをクリックした先のページにあります
これから、半径 r の球の体積Vは、
体積V=(4π/3) r3
になることがわかりました。
この様に、要素に分割して総和を計算することが「積分」をするということです。
【別解】
以下の様に、直接に球の体積を求めることもできます。
先ず、半径1の球の体積を計算します。
これで、半径1の球の体積が計算できました。
これから、半径 r の球の体積Vは、
体積V=(4π/3) r3
になることがわかりました。
リンク:
球の体積・表面積の求め方!公式や覚え方、なぜそうなるかを徹底解説!
高校数学の目次

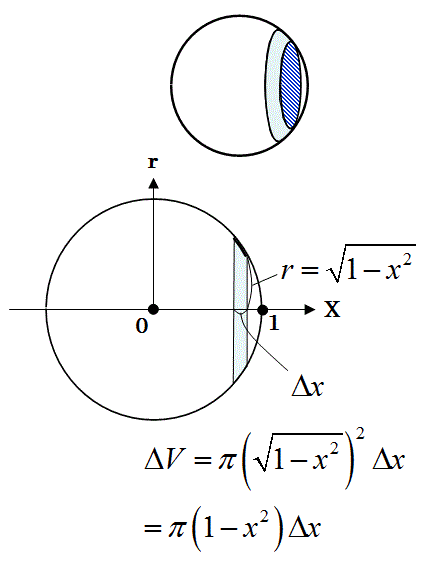


初めましてになります。球の体積について疑問になり検索していたらこちらにたどりつきました。クリガラと申します。管理人様の途中の計算式を自分で解いていたところ
返信削除= 4π(Δr)3 n(n+(1/2))(n+1)/3
→ 4π r3/3
( r=n(Δr))
のところでnΔr3=r3 までは解きましたが、残りの(n+1/2)(n+1)/3のところをどうしたら良いのか悩んでいまして、、お時間ありましたら教えてください。。よろしくお願いいたします。
= 4π(Δr)3 n(n+(1/2))(n+1)/3
削除→ 4π r3/3
の部分の説明を、もう少し詳しく説明するように説明を追加しました。