以下の問題は、第１次の解を、「ひし形の対角線の直交の公式」を使って第２次の解に変換しましょう。
【問１】
円（ｘ２＋ｙ２＝１）に対して、
接点Ａ（ａ１，ａ２）から引いた接線と接点Ｂ（ｂ１，ｂ２）から引いた接線の交点Ｐ（ｘ，ｙ）を求めよ。
（接点Ａから引いた接線と接点Ｂから引いた接線の交点Ｐは、円Ｏの、極線ＡＢに対する極と呼びます。）
【解答】
円の式を、以下の式１のｆ（ｘ，ｙ）＝０であらわす。
接点ＡとＢとに、以下の式２と３が成り立つ。
円の接線の公式により、接点ＡとＢとの２つの接線は、以下の式４と５であらわせる。
式４と５を連立させて、２つの接線の交点Ｐ（ｘ，ｙ）を求める。
解の式１０は、これ以上単純にできない完成した解です。
（第１の解答おわり）
この式１０であらわされるベクトルPと、
ベクトルM＝（ベクトルａ＋ｂ）／２
が平行である事が以下の計算で確かめられる。
先ず、ベクトルａとｂを反時計回りに９０度回転したベクトルａvとベクトルｂvを考える。
（ベクトルの平行性の確認おわり）
解答の式１０の分子は、
（ベクトルａv）－（ベクトルｂv）
をあらわす。それは、以下の式の通りです。
この式は、以下のひし形の対角線の直交の公式によっても、
（ベクトルａ）＋（ベクトルｂ）
に平行になる事がわかります。
【ひし形の対角線の直交の公式】
以下の式で与えられる「ひし形の対角線の直交の公式」を覚えて使いましょう。
式（２）－式（３）：
「この式６の左右の項が互いに置き換えられる」
ということが、
ひし形の対角線の直交の公式です。
この公式は、以下の図の線分ＯＫの傾きが線分ＯＨの傾きの逆数×（－１）である、ことを示す公式です。
----ひし形の対角線の直交の公式おわり-----------
【２重平行四辺形の面積の公式】
ここで、もう１つの式７で与えられる、２重平行四辺形の面積の公式も覚えて使いましょう。（これは恒等式です）
この式７の公式は、右辺から左辺を導く公式として覚えましょう。
この式７の公式は、以下の図の平行四辺形の面積をあらわすベクトルの外積の間の関係です。
----２重平行四辺形の面積の公式おわり-----------
（９０度回転したベクトルを利用した面積の公式）
この２重平行四辺形の面積の公式は、ベクトルAとBを反時計回りに９０度回転したベクトルAvとBvを使って、以下の式であらわせます。
（９０度回転したベクトルを利用した面積の公式おわり）
解の式１０は、これ以上単純にできない完成した解でした。
しかし、それは、（ベクトルａ）＋（ベクトルｂ）に平行なので、その式の定数倍の式でも解が表せると考えます。
以下の図の様に、この解１０をベクトルであらわすと：
この式（１０）は、上式の様にベクトルＯＫの２倍をＯＫの長さの二乗で割り算した形の式に変換できることがわかります。
図形とベクトルを使って解を表現すると、この様に解を求める見通しが良くなるので、方程式の解を得たら、その解を可能な限り図形とベクトルを使って表現してまとめるよう心がけましょう。
この様に解が変換できることが分かったので、次に、この交点Ｐの式１０の解を、２重平行四辺形の面積の公式（７）とひし形の対角線の直交の公式（６）を使って変換することを試みましょう。
式８に、式７（の逆）を代入して変形する。
この式１１に、公式６を代入する。
次に、式９に、式７（の逆）を代入して変形する。
この式１３に公式６を代入する。
式１２と式１４をまとめる。
（第２の解答おわり）
（補足１）
ここで、第２の解答で式１５の形の解を求めましたが、
第１の解答で得た式１０の形の解と、式１５の形の解とは、どちらが優れている（単純な）解であると言うことが出来ない対等な解です。
問１を解く解答者の意思に従って、問１の解は、式１０にも、また、式１５にもなります。
全く対等な解が、式１０の形と式１５の形との２つの形であらわせます。その２つの解の間の変換は、ひし形の対角線の直交の公式を用いて行なえます。
（補足２）
式１５は、２つの接線の交点Ｐの位置ベクトルＯＰは、点Ａと点Ｂの中点Ｍの位置ベクトルＯＭに平行であることを示している。
また、式１５は、点Ａと点Ｂの中点Ｍの位置が円のグラフに近づけば、点Ｐが中点Ｍに近づくことを示している。
（補足３）
式１０で交点Ｐ（ｘ，ｙ）の座標値が計算された時点で、線分ＯＰの傾きは、線分ＯＨの傾きの逆数×（－１）になっているので、ひし形の対角線の直交の公式（式６）によって、線分ＯＫの傾き（＝線分ＯＭの傾き）に等しいことがわかります。
リンク：
ベクトルで円の二接線の交点（極）を求める（解の変換）
複素数平面が、円の２つの接線の交点問題を簡単にする
高校数学の目次
【問１】
円（ｘ２＋ｙ２＝１）に対して、
接点Ａ（ａ１，ａ２）から引いた接線と接点Ｂ（ｂ１，ｂ２）から引いた接線の交点Ｐ（ｘ，ｙ）を求めよ。
（接点Ａから引いた接線と接点Ｂから引いた接線の交点Ｐは、円Ｏの、極線ＡＢに対する極と呼びます。）
【解答】
円の式を、以下の式１のｆ（ｘ，ｙ）＝０であらわす。
（第１の解答おわり）
この式１０であらわされるベクトルPと、
ベクトルM＝（ベクトルａ＋ｂ）／２
が平行である事が以下の計算で確かめられる。
先ず、ベクトルａとｂを反時計回りに９０度回転したベクトルａvとベクトルｂvを考える。
解答の式１０の分子は、
（ベクトルａv）－（ベクトルｂv）
をあらわす。それは、以下の式の通りです。
（ベクトルａ）＋（ベクトルｂ）
に平行になる事がわかります。
【ひし形の対角線の直交の公式】
以下の式で与えられる「ひし形の対角線の直交の公式」を覚えて使いましょう。
式（２）－式（３）：
ということが、
ひし形の対角線の直交の公式です。
この公式は、以下の図の線分ＯＫの傾きが線分ＯＨの傾きの逆数×（－１）である、ことを示す公式です。
----ひし形の対角線の直交の公式おわり-----------
【２重平行四辺形の面積の公式】
ここで、もう１つの式７で与えられる、２重平行四辺形の面積の公式も覚えて使いましょう。（これは恒等式です）
この式７の公式は、以下の図の平行四辺形の面積をあらわすベクトルの外積の間の関係です。
（９０度回転したベクトルを利用した面積の公式）
この２重平行四辺形の面積の公式は、ベクトルAとBを反時計回りに９０度回転したベクトルAvとBvを使って、以下の式であらわせます。
解の式１０は、これ以上単純にできない完成した解でした。
しかし、それは、（ベクトルａ）＋（ベクトルｂ）に平行なので、その式の定数倍の式でも解が表せると考えます。
以下の図の様に、この解１０をベクトルであらわすと：
図形とベクトルを使って解を表現すると、この様に解を求める見通しが良くなるので、方程式の解を得たら、その解を可能な限り図形とベクトルを使って表現してまとめるよう心がけましょう。
この様に解が変換できることが分かったので、次に、この交点Ｐの式１０の解を、２重平行四辺形の面積の公式（７）とひし形の対角線の直交の公式（６）を使って変換することを試みましょう。
式８に、式７（の逆）を代入して変形する。
（補足１）
ここで、第２の解答で式１５の形の解を求めましたが、
第１の解答で得た式１０の形の解と、式１５の形の解とは、どちらが優れている（単純な）解であると言うことが出来ない対等な解です。
問１を解く解答者の意思に従って、問１の解は、式１０にも、また、式１５にもなります。
全く対等な解が、式１０の形と式１５の形との２つの形であらわせます。その２つの解の間の変換は、ひし形の対角線の直交の公式を用いて行なえます。
（補足２）
式１５は、２つの接線の交点Ｐの位置ベクトルＯＰは、点Ａと点Ｂの中点Ｍの位置ベクトルＯＭに平行であることを示している。
また、式１５は、点Ａと点Ｂの中点Ｍの位置が円のグラフに近づけば、点Ｐが中点Ｍに近づくことを示している。
（補足３）
式１０で交点Ｐ（ｘ，ｙ）の座標値が計算された時点で、線分ＯＰの傾きは、線分ＯＨの傾きの逆数×（－１）になっているので、ひし形の対角線の直交の公式（式６）によって、線分ＯＫの傾き（＝線分ＯＭの傾き）に等しいことがわかります。
リンク：
ベクトルで円の二接線の交点（極）を求める（解の変換）
複素数平面が、円の２つの接線の交点問題を簡単にする
高校数学の目次
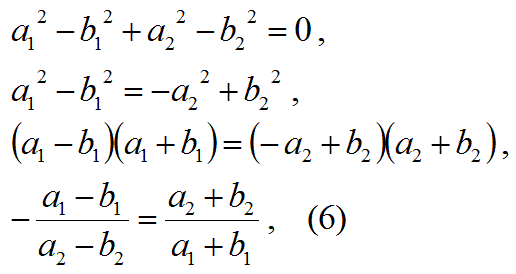
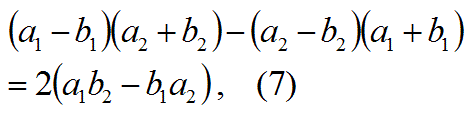
0 件のコメント:
コメントを投稿