以下の連立方程式を考える。
この連立方程式は、以下のように定義したベクトルの内積の式5と6であらわすことができる。
この連立方程式を以下のようにしてベクトルを使って解く。
(解答はじめ)
先ず、式3が成り立つので、以下の式7が成り立つ。
すなわち、ベクトルaとcの和のベクトルと、ベクトルaとcの差のベクトルの内積が0になり、それらのベクトルが互いに垂直である。
(これは、以下の図のひし形の対角線の直交の公式をあらあわす)
ベクトルzを、互いに垂直なベクトルの要素に分解することは容易にできるので、以下でその作業を行う。
ベクトルaとcの和のベクトルに平行な単位ベクトルsと、
ベクトルcとaの差のベクトルに平行な単位ベクトルtを考える。
ベクトルzを、単位ベクトルsとtに平行な要素に分解してあらわす。
ここで得られた式8は、ベクトルzの解である。
この式8をベクトルaの要素とベクトルcの要素で整理すると、もっと複雑な、扱いにくい式になる。
ベクトルは、この式8のように、互いに垂直なベクトル毎にまとめる方が単純な式になる。
この式8が、この計算結果によるzの解をあらわす一番単純な式である。
(解答おわり)
(補足1)
この式8が成り立つことは、以下のようにして確認できる。
問題の式5と式6は以下の式に変形できる。
式8が、この式を満足するので、式8が成り立っている。
(補足2)
この問題のzの解は、以下の式9であらわすこともできる。
(式8を式9に変換する)
この式9は、以上とは異なる発想で解いた結果の式であり、式8と等しい式です。以下の計算によって、式8を式9に変換できます。
こうして、式8を式9に変換できました。
(変換おわり)
式8も式9も、どちらが優れている(単純な)解だと言うことが出来ない、対等な解です。
式9は、ベクトルaに垂直なベクトルavと、ベクトルcに垂直なベクトルcvを加えてあらわした、使うベクトルの数が多い式ですが、式8よりも計算がし易い式であるとも言えそうです。
この式9は、直ぐには導き出せないので、以下のように整理して公式として覚えておいてください。
【ベクトル方程式の公式1】
以下の連立ベクトル方程式の式a1とa2があるとき:
この連立ベクトル方程式の解は:
である。
なぜなら、式a1と式a2のベクトルzに式a3を代入すると、以下の通り、式a1とa2を満足するからである。
(公式おわり)
【ベクトル方程式の公式2】
以下のベクトルzとaとbがあるとき:
ベクトルaとbを反時計回りに90度回転したベクトルavとベクトルbvを利用して、以下の関係が成り立つ。
(公式おわり)
この公式を図で表すと以下の図になります。
(補足:公式2の言い換え)
ベクトルuとwを以下の式で定義する。
このベクトルuとwを使って公式2が以下の形の式であらわせる。
公式2はこの形の式に言い換えた方が覚えやすいかもしれない。
【連立方程式の解の公式3】
以下の連立方程式の解の公式3もあります。
これらのベクトルを使って連立方程式10と11をまとめて上のベクトル方程式15が得られます。
すなわち、ベクトルの視点で見ると、連立方程式10と11は、式15のベクトル方程式をあらわしていると見ることができます。
ここで、ベクトルaとベクトルbと、それらを反時計回りに90°回転させたベクトルavとベクトルbvが下図のように描けます。
反時計回りに90°回転させたベクトルavとベクトルbvが以下の式16と17であらわせます。
以下の式の内積の計算により、xの解の式18とyの解の式19が得られます。
(補足)
ベクトルaを反時計回りに90度回転した単位ベクトルav=fを、
更に反時計回りに90度回転した単位ベクトルfvは-aになる。
そのため、ベクトルの内積av・bを、
両ベクトルを一緒に反時計回りに90度回転して内積した値は同じ値になるが、
その関係は、以下の式であらわされる。
av・b=-a・bv
すなわち、以下の式20が成り立ちます。
(補足おわり)
結局、ベクトル方程式15であらわした連立方程式10と11の未知数xとyが、上の式18と式19で計算できる、
連立方程式の解の公式3が導けました。
この解の公式3の方が覚えやすい公式かもしれない。
この公式3は、以下の図で表せる。
リンク:
円の極の座標の解の変換
複素数平面が、円の2つの接線の交点問題を簡単にする
高校数学の目次
この連立方程式は、以下のように定義したベクトルの内積の式5と6であらわすことができる。
この連立方程式を以下のようにしてベクトルを使って解く。
(解答はじめ)
先ず、式3が成り立つので、以下の式7が成り立つ。
すなわち、ベクトルaとcの和のベクトルと、ベクトルaとcの差のベクトルの内積が0になり、それらのベクトルが互いに垂直である。
(これは、以下の図のひし形の対角線の直交の公式をあらあわす)
ベクトルzを、互いに垂直なベクトルの要素に分解することは容易にできるので、以下でその作業を行う。
ベクトルaとcの和のベクトルに平行な単位ベクトルsと、
ベクトルcとaの差のベクトルに平行な単位ベクトルtを考える。
ベクトルzを、単位ベクトルsとtに平行な要素に分解してあらわす。
ここで得られた式8は、ベクトルzの解である。
この式8をベクトルaの要素とベクトルcの要素で整理すると、もっと複雑な、扱いにくい式になる。
ベクトルは、この式8のように、互いに垂直なベクトル毎にまとめる方が単純な式になる。
この式8が、この計算結果によるzの解をあらわす一番単純な式である。
(解答おわり)
(補足1)
この式8が成り立つことは、以下のようにして確認できる。
問題の式5と式6は以下の式に変形できる。
式8が、この式を満足するので、式8が成り立っている。
(補足2)
この問題のzの解は、以下の式9であらわすこともできる。
(式8を式9に変換する)
この式9は、以上とは異なる発想で解いた結果の式であり、式8と等しい式です。以下の計算によって、式8を式9に変換できます。
(変換おわり)
式8も式9も、どちらが優れている(単純な)解だと言うことが出来ない、対等な解です。
式9は、ベクトルaに垂直なベクトルavと、ベクトルcに垂直なベクトルcvを加えてあらわした、使うベクトルの数が多い式ですが、式8よりも計算がし易い式であるとも言えそうです。
この式9は、直ぐには導き出せないので、以下のように整理して公式として覚えておいてください。
【ベクトル方程式の公式1】
以下の連立ベクトル方程式の式a1とa2があるとき:
この連立ベクトル方程式の解は:
なぜなら、式a1と式a2のベクトルzに式a3を代入すると、以下の通り、式a1とa2を満足するからである。
(公式おわり)
【ベクトル方程式の公式2】
以下のベクトルzとaとbがあるとき:
ベクトルaとbを反時計回りに90度回転したベクトルavとベクトルbvを利用して、以下の関係が成り立つ。
この公式を図で表すと以下の図になります。
(補足:公式2の言い換え)
ベクトルuとwを以下の式で定義する。
このベクトルuとwを使って公式2が以下の形の式であらわせる。
公式2はこの形の式に言い換えた方が覚えやすいかもしれない。
【連立方程式の解の公式3】
以下の連立方程式の解の公式3もあります。
ここで、ベクトルaとベクトルbと、それらを反時計回りに90°回転させたベクトルavとベクトルbvが下図のように描けます。
(補足)
ベクトルaを反時計回りに90度回転した単位ベクトルav=fを、
更に反時計回りに90度回転した単位ベクトルfvは-aになる。
そのため、ベクトルの内積av・bを、
両ベクトルを一緒に反時計回りに90度回転して内積した値は同じ値になるが、
その関係は、以下の式であらわされる。
av・b=-a・bv
すなわち、以下の式20が成り立ちます。
結局、ベクトル方程式15であらわした連立方程式10と11の未知数xとyが、上の式18と式19で計算できる、
連立方程式の解の公式3が導けました。
この公式3は、以下の図で表せる。
リンク:
円の極の座標の解の変換
複素数平面が、円の2つの接線の交点問題を簡単にする
高校数学の目次



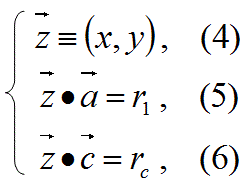




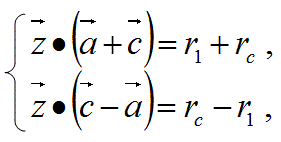
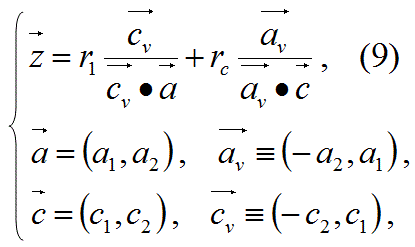






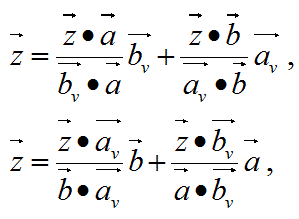




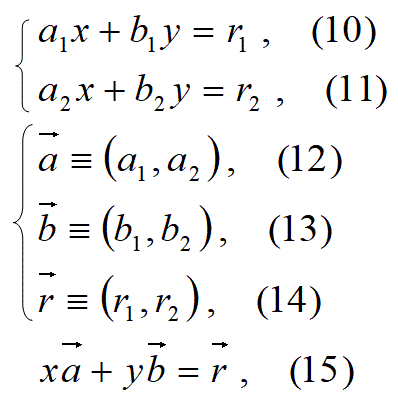






0 件のコメント:
コメントを投稿