【証明1】
この式1の左辺と右辺のベクトルの成分を比較する。
そのため、式1の右辺と左辺は等しい。
式2は、式1のベクトルbを-bベクトルに置き換えるだけで成り立つ。
(証明1おわり)
【証明2】
以下の図を参照して、ベクトルの分解の公式を使ってベクトルを変換する。
計算を媒介するベクトルpを使って、
以下の様にベクトルを変換する計算をする。
次に、ベクトルpを(ベクトルa-ベクトルb)にすると:
式3bが求められた。
式3bも、他の、ベクトルの変換の式である。
(証明2おわり)
この証明2の過程で得た式3が、式1よりも、より根源的な公式です。しかも、当たり前の形をしていて覚えやすい。そのため、式1を覚えるよりも先に式3を覚えるべきです。
なお、この式3の両辺には、形が異なるが平行なベクトルを選んで式に当てはめる。
(補足1)
この公式は、ベクトルa+bが、ベクトルu+wに平行である事を示していますが、
ベクトルaの偏角<bの偏角の場合に、平行になり、
ベクトルaの偏角>bの偏角の場合に、逆平行になり向きが逆になり、
状況が異なりますので注意する必要があります。
(補足2)
この公式(式1)は、
であることをあらわしています。
これは、ひし形の対角線の直交の公式をあらわしています。
そのため、この公式は、ひし形の対角線の直交の公式を言い換えた公式であるという意味を持ちます。
リンク:
ひし形の対角線の直交の公式
円の極の座標の解の変換
複素数平面が、円の2つの接線の交点問題を簡単にする
高校数学の目次


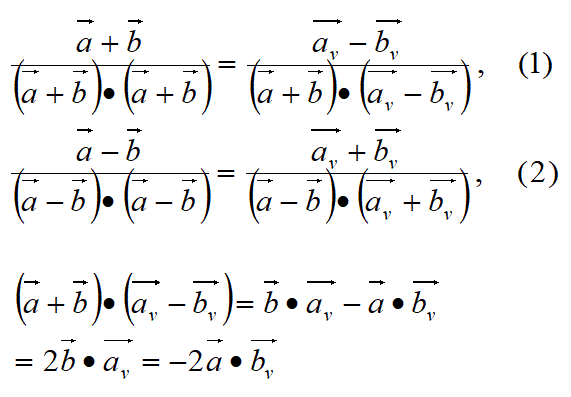



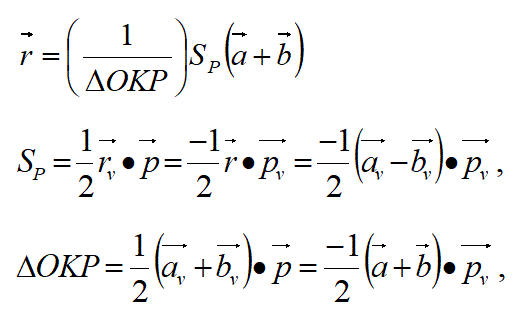

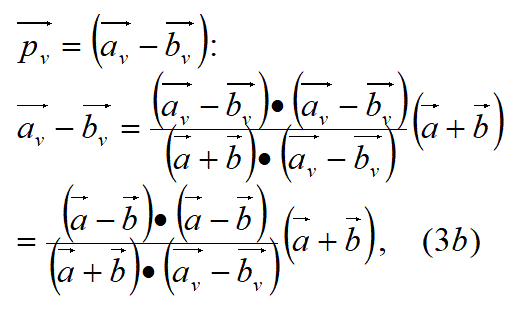


0 件のコメント:
コメントを投稿