

複素数の計算を推進する以下の公式を導きだしましょう。
(第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
(優先順位の2位以下のこと)
それよりは優先順位が低いことですが、以下のような、複素数平面の計算の公式の導き出し方を身に付けると、少し計算が推進されますので、以下の公式も、簡単に導き出せるようになればとても良いと思います。
以下の公式も使う場合が多いと思います。
これは、ベクトルの2乗の差を合成ベクトルの内積に変える公式です。
【合成ベクトルの内積をベクトルの2乗の差に変える公式】
この公式は、「余弦定理に類似した中線の式」でもあります。
この公式は、複素数平面での複素数の計算よりもベクトルの計算を利用した方が速やかに式を導き出せるように思います。
また、以下の式も大切です。
以下の式は、
(2つのベクトルの貼る平行四辺形の面積S)の(2i倍)
の式です。
この式を包含する以下の式が成り立ちます。
任意の実数kに関して:
が成り立ちます。
それは、この式が以下の図の平行四辺形の面積の(-1倍)を表すからです。
先に記述した平行四辺形の面積(の2i倍)の式は、以下の式に変形できます。
この式は、2重平行四辺形の面積の公式を表しています。
【2重平行四辺形の面積の公式】
平行四辺形ABCDに外接する図のような平行四辺形CDEFの面積は、ベクトルAとBの張る平行四辺形ABCDの面積の2倍です。
(以上が2重平行四辺形の面積の公式)
(この式の上から2行目の式と3行目の式は、|α|=|β|の場合には、右辺が第1項のみになります。それを利用して、以下の公式が使えます。)
実数係数kを利用してβを下式のように絶対値がαと同じ複素数β’であらわします。

以上の公式で、以下の部分が特に重要です。
上の公式において、
特に、以下の公式を注目して覚えると、式の変形に便利と思います。
また、この公式の意味は:
ということをあらわし、
合成ベクトル(α-β’)と、
合成ベクトル(α+β’)
の内積が0になり、
2つの合成ベクトルが直交する事をあらわしています。
(ベクトルでの「ひし形の対角線の直交の公式」と同じです)
すなわち、
公式:
という公式でもあります。
【ひし形の対角線の直交の公式】
下図のひし形OAKBの2つの対角線OKとABが互いに直交することが、
以下の図の線分OKの傾きが、線分ABに平行な線分OHの傾きの逆数×(-1)である、ことにより証明できます。

同様に、以下の公式も使えます。
ただし、以下の公式でのkは、βを以下の関係のβ’に置き換える実数係数です。


以上の式に対しては、任意の実数θとεに関して、
α⇒αexp(iθ)
β⇒βexp(iε)
という式の置き換えを行えます。
その置き換えでは、以下の式の左辺が変化しないので、以下の式が成り立ちます。
【公式の整理】
ここで得られた公式は:
です。
この2つの公式は、以下の1つの式にまとめられます。
この式は、
ベクトル(α+β)とベクトル(β-α)が直交してベクトルの内積が0になる場合は、αの絶対値とβの絶対値が等しい場合である事を表しています。
また、
ベクトル(α+β)とベクトル(β-α)が張る平行四辺形の面積は、ベクトルαとベクトルβが張る平行四辺形の面積Sの2倍である事を表しています。
(補足)
αの絶対値とβの絶対値が等しい場合は、ベクトル(α+β)とベクトル(β-α)が直交するので、以下の関係が成り立つ。
リンク:
高校数学の目次
(第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
(優先順位の2位以下のこと)
それよりは優先順位が低いことですが、以下のような、複素数平面の計算の公式の導き出し方を身に付けると、少し計算が推進されますので、以下の公式も、簡単に導き出せるようになればとても良いと思います。
【合成ベクトルの内積をベクトルの2乗の差に変える公式】
この公式は、複素数平面での複素数の計算よりもベクトルの計算を利用した方が速やかに式を導き出せるように思います。
また、以下の式も大切です。
以下の式は、
(2つのベクトルの貼る平行四辺形の面積S)の(2i倍)
の式です。
この式を包含する以下の式が成り立ちます。
任意の実数kに関して:
それは、この式が以下の図の平行四辺形の面積の(-1倍)を表すからです。
先に記述した平行四辺形の面積(の2i倍)の式は、以下の式に変形できます。
【2重平行四辺形の面積の公式】
平行四辺形ABCDに外接する図のような平行四辺形CDEFの面積は、ベクトルAとBの張る平行四辺形ABCDの面積の2倍です。
(以上が2重平行四辺形の面積の公式)
(この式の上から2行目の式と3行目の式は、|α|=|β|の場合には、右辺が第1項のみになります。それを利用して、以下の公式が使えます。)
実数係数kを利用してβを下式のように絶対値がαと同じ複素数β’であらわします。

以上の公式で、以下の部分が特に重要です。
上の公式において、
特に、以下の公式を注目して覚えると、式の変形に便利と思います。
ということをあらわし、
合成ベクトル(α-β’)と、
合成ベクトル(α+β’)
の内積が0になり、
2つの合成ベクトルが直交する事をあらわしています。
(ベクトルでの「ひし形の対角線の直交の公式」と同じです)
すなわち、
公式:
という公式でもあります。
【ひし形の対角線の直交の公式】
下図のひし形OAKBの2つの対角線OKとABが互いに直交することが、
以下の図の線分OKの傾きが、線分ABに平行な線分OHの傾きの逆数×(-1)である、ことにより証明できます。

同様に、以下の公式も使えます。
ただし、以下の公式でのkは、βを以下の関係のβ’に置き換える実数係数です。


以上の式に対しては、任意の実数θとεに関して、
α⇒αexp(iθ)
β⇒βexp(iε)
という式の置き換えを行えます。
その置き換えでは、以下の式の左辺が変化しないので、以下の式が成り立ちます。
【公式の整理】
ここで得られた公式は:
です。
この2つの公式は、以下の1つの式にまとめられます。
この式は、
ベクトル(α+β)とベクトル(β-α)が直交してベクトルの内積が0になる場合は、αの絶対値とβの絶対値が等しい場合である事を表しています。
また、
ベクトル(α+β)とベクトル(β-α)が張る平行四辺形の面積は、ベクトルαとベクトルβが張る平行四辺形の面積Sの2倍である事を表しています。
(補足)
αの絶対値とβの絶対値が等しい場合は、ベクトル(α+β)とベクトル(β-α)が直交するので、以下の関係が成り立つ。
リンク:
高校数学の目次













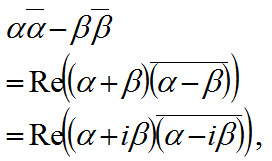



0 件のコメント:
コメントを投稿