【課題】
ベクトルの分解の公式と合成の公式に対応して、複素数平面の複素数の分解の公式と合成の公式が考えられます。
【ベクトルの分解の公式】
ベクトルaとbを反時計回りに90度回転した単位ベクトルavと単位ベクトルbvを加えて考えると、以下の図の関係がある。
ベクトルOZは、上図の式、又は、以下の式で、ベクトルaとbであらわせる。
この式がベクトルの分解の公式である。
【図形で説明】
ベクトルの分解の公式は、以下の図の様にあらわせる。
この、ベクトルの分解の公式に対応して、複素数平面の複素数の分解の公式が以下の式であらわせる。
【複素数の分解の公式】
この複素数の分解の公式は、以下の式の変形によって証明できる。
(証明おわり)
【複素数の合成の公式】
以下の形の式の複素数があれば、それは複素数Zに合成できる。
【証明開始】
この式の左辺が以下のように変形できる。
(証明おわり)
リンク:
複素数平面のベクトル方程式(1)の解答
2次元ベクトルの合成の公式と分解の公式と2つのベクトルの大きさの積の三平方の定理
高校数学の目次
ベクトルの分解の公式と合成の公式に対応して、複素数平面の複素数の分解の公式と合成の公式が考えられます。
【ベクトルの分解の公式】
ベクトルaとbを反時計回りに90度回転した単位ベクトルavと単位ベクトルbvを加えて考えると、以下の図の関係がある。
ベクトルOZは、上図の式、又は、以下の式で、ベクトルaとbであらわせる。
この式がベクトルの分解の公式である。
【図形で説明】
ベクトルの分解の公式は、以下の図の様にあらわせる。
この、ベクトルの分解の公式に対応して、複素数平面の複素数の分解の公式が以下の式であらわせる。
【複素数の分解の公式】
この複素数の分解の公式は、以下の式の変形によって証明できる。
(証明おわり)
【複素数の合成の公式】
以下の形の式の複素数があれば、それは複素数Zに合成できる。
【証明開始】
この式の左辺が以下のように変形できる。
(証明おわり)
リンク:
複素数平面のベクトル方程式(1)の解答
2次元ベクトルの合成の公式と分解の公式と2つのベクトルの大きさの積の三平方の定理
高校数学の目次






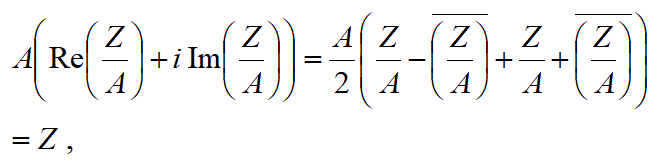
0 件のコメント:
コメントを投稿