佐藤の数学教科書「三角関数」編の勉強
【問１】難問
三角形ＡＢＣにおいて
∠Ａ≠０であり、
２ｃｏｓＡ＋ｃｏｓＢ＋ｃｏｓＣ＝２ （式１）
が成り立っていれば、
２ｓｉｎＡ＝ｓｉｎＢ＋ｓｉｎＣ （式２）
が成り立つことを証明せよ。
（注意）この問題は、「加法定理」の例題として出されていましたが、
必ずしも加法定理を使って解くものとは限らない。
以下に説明する証明の計算でも加法定理は使わないで証明する。
そして、三角形の正弦定理ｓｉｎＡ／ａ＝１／（２Ｒ）・・・を使うことが、解答のために本質的に重要。
【重要な注意】
式１のｃｏｓの式を、加法定理その他の三角関数の変換定理で変換しても、式２に至りません。そのように、三角関数の計算の自由度は低いです（加法定理などで変換できる式も少しはありますが）。
そのため、三角関数（特に三角形の角度の三角関数）の問題を自由に解くためには、三角関数の式を、なるべく、ベクトルの式やｘｙ座標の式に変えて計算する必要があります。
（予備知識）
受験問題のときは、三角形の角度のｓｉｎ、ｃｏｓ（三角関数）の式の証明問題は、三角関数の式をベクトルの式であらわして、図形で考えます。ベクトルを利用して図形の問題を考えることは、計算の見通しを良くするからです。
（問題をより易しい問題に変換してから解くこと）
証明すべき対象の
２ｓｉｎＡ＝ｓｉｎＢ＋ｓｉｎＣ （式２）
を直接証明しようとする前に、この式を、図形の問題として、わかる限り、問題をかみくだいて易しい問題に変換しておいてから問題を解きます。
三角形の正弦定理ｓｉｎＡ／ａ＝１／（２Ｒ）・・・を使うと、
２ｓｉｎＡ＝ｓｉｎＢ＋ｓｉｎＣ （式２）
は、以下の式に書き直せます。
２（ａ／（２Ｒ））＝（ｂ／（２Ｒ））＋（ｃ／（２Ｒ））
２ａ－ｂ－ｃ＝０ （式３）
問題がここまで易しくなります。
三角形の辺の長さの関係の式３を証明すれば良いです。
（式１の変形の方針）
正弦定理を使って、証明するべき式２のｓｉｎを消去して易しくしたように、ベクトルの内積の式を使って、元の条件の、式１のｃｏｓを消去します。
（ｃｏｓを消去する場合に、余弦定理を使うよりは、計算の見通しの良いベクトルの内積の式を使います）
この式を使って、式１を以下のように書き直します。
この式の解は：
２ａ－ｂ－ｃ＝０， （式４）
又は、
ベクトルMとNの内積＝ｂｃ， （式５）
です。
式５が成り立つ場合に、式４（式３）が成り立つとは限らない。
式５では、
ベクトルMとNの内積＝ｂｃ
になり、
その場合は
∠A＝０
である。
前提条件が
∠Ａ≠０
であるため、式５は不適であり、式４が成り立つ。
よって、
∠A＞０の場合に、式３と同じ式４が成り立つ。
（証明おわり）
【問２】
（問２が作られた背景）
問１を解く方法を発見した後で考えることは、
「発見したその解き方は、他の問題を解くのにも使える適用範囲の広い解き方なのだろうか？」
という疑問が湧くと思います。
しかし、そういう疑問に答えてくれる人はごくわずかしかいなく、高校の数学の先生や予備校の数学の先生が答えてくれ可能性は低く、ましてや、ネットでの質問サイトからまともな答えが得られるとは考えられない、と思います。
自分が分からない問題に素直に分からないと答えられる率直な先生、すなわち、大学の数学の先生からは、まともな答えが受け取れるだろうと思います。それ以外にあてに出来る人は、そのような疑問を抱く、数学が好きな友人か、また、そのような疑問を抱いた自分自身だと思います。
それで、この疑問を具体化した、以下の問２を考え、自分自身で、この問題を解くようにしましょう。
（問２の問題の記述）
三角形ＡＢＣにおいて
∠Ａ≠０,∠B≠０,∠C≠０,
であり、以下の式１が成り立つときに式２が成り立つように、
式１と式２の係数ｘ、ｙ、ｚ、ｓ、ｔ、ｕの値を定めよ。
（解答開始）
先ず、式２を、正弦定理を使って、上の式３に変換します。
次に、式１を以下のようにベクトルの内積であらわします。
この式４から、式３の形の解を得るための条件の１つは、
以下の式５と式６である。
この式５と式６が成り立つならば、以下のように、式４が式７に変形できる。
∠Ａ≠０であるので、
は０にはならない。
そのため、式７から、式８が得られる。
この式８が式２に等しくなる条件は、以下の式９～式１２で与えられる。
式５と式６と、これらの式９～式１２が、式１が成り立つときに式２が成り立つ、係数ｘ、ｙ、ｚ、ｓ、ｔ、ｕの値の１つである。
（式４から、式３の形の解を得るための条件の全てが式５と式６であるとまでは証明しなかったため、これ以外の解がある可能性が排除できていない。特に、式５と式６が成り立っていなくても、式３の係数を適切に選べば（ただし、その係数は角度Ａ，Ｂ，Ｃに応じて変わるだろうが）式３はいつでも成り立たせることができると言える。）
（解答おわり）
（補足）
この問題２を解いた結果、式１の形の条件から必ず式２の形の式が導けるわけでは無いことがわかった。式１から式２が得られる場合は、式５と式６と式９～式１２が成り立つ場合に限られることがわかった。
一般的な形の式１を式２の形に変換する公式は無い。
よって、問題１において、式１から式２が得られることの証明方法は、それぞれの式を単純化して比較する分析の結果、両式が偶然に一致していることを確認する、上記の解き方で良いことがわかった。
リンク：
別解
複素数平面を使った解答
高校数学の目次
【問１】難問
三角形ＡＢＣにおいて
∠Ａ≠０であり、
２ｃｏｓＡ＋ｃｏｓＢ＋ｃｏｓＣ＝２ （式１）
が成り立っていれば、
２ｓｉｎＡ＝ｓｉｎＢ＋ｓｉｎＣ （式２）
が成り立つことを証明せよ。
（注意）この問題は、「加法定理」の例題として出されていましたが、
必ずしも加法定理を使って解くものとは限らない。
以下に説明する証明の計算でも加法定理は使わないで証明する。
そして、三角形の正弦定理ｓｉｎＡ／ａ＝１／（２Ｒ）・・・を使うことが、解答のために本質的に重要。
【重要な注意】
式１のｃｏｓの式を、加法定理その他の三角関数の変換定理で変換しても、式２に至りません。そのように、三角関数の計算の自由度は低いです（加法定理などで変換できる式も少しはありますが）。
そのため、三角関数（特に三角形の角度の三角関数）の問題を自由に解くためには、三角関数の式を、なるべく、ベクトルの式やｘｙ座標の式に変えて計算する必要があります。
（予備知識）
受験問題のときは、三角形の角度のｓｉｎ、ｃｏｓ（三角関数）の式の証明問題は、三角関数の式をベクトルの式であらわして、図形で考えます。ベクトルを利用して図形の問題を考えることは、計算の見通しを良くするからです。
（問題をより易しい問題に変換してから解くこと）
証明すべき対象の
２ｓｉｎＡ＝ｓｉｎＢ＋ｓｉｎＣ （式２）
を直接証明しようとする前に、この式を、図形の問題として、わかる限り、問題をかみくだいて易しい問題に変換しておいてから問題を解きます。
三角形の正弦定理ｓｉｎＡ／ａ＝１／（２Ｒ）・・・を使うと、
２ｓｉｎＡ＝ｓｉｎＢ＋ｓｉｎＣ （式２）
は、以下の式に書き直せます。
２（ａ／（２Ｒ））＝（ｂ／（２Ｒ））＋（ｃ／（２Ｒ））
２ａ－ｂ－ｃ＝０ （式３）
問題がここまで易しくなります。
三角形の辺の長さの関係の式３を証明すれば良いです。
（式１の変形の方針）
正弦定理を使って、証明するべき式２のｓｉｎを消去して易しくしたように、ベクトルの内積の式を使って、元の条件の、式１のｃｏｓを消去します。
（ｃｏｓを消去する場合に、余弦定理を使うよりは、計算の見通しの良いベクトルの内積の式を使います）
この式を使って、式１を以下のように書き直します。
２ａ－ｂ－ｃ＝０， （式４）
又は、
ベクトルMとNの内積＝ｂｃ， （式５）
です。
式５が成り立つ場合に、式４（式３）が成り立つとは限らない。
式５では、
ベクトルMとNの内積＝ｂｃ
になり、
その場合は
∠A＝０
である。
前提条件が
∠Ａ≠０
であるため、式５は不適であり、式４が成り立つ。
よって、
∠A＞０の場合に、式３と同じ式４が成り立つ。
（証明おわり）
【問２】
（問２が作られた背景）
問１を解く方法を発見した後で考えることは、
「発見したその解き方は、他の問題を解くのにも使える適用範囲の広い解き方なのだろうか？」
という疑問が湧くと思います。
しかし、そういう疑問に答えてくれる人はごくわずかしかいなく、高校の数学の先生や予備校の数学の先生が答えてくれ可能性は低く、ましてや、ネットでの質問サイトからまともな答えが得られるとは考えられない、と思います。
自分が分からない問題に素直に分からないと答えられる率直な先生、すなわち、大学の数学の先生からは、まともな答えが受け取れるだろうと思います。それ以外にあてに出来る人は、そのような疑問を抱く、数学が好きな友人か、また、そのような疑問を抱いた自分自身だと思います。
それで、この疑問を具体化した、以下の問２を考え、自分自身で、この問題を解くようにしましょう。
（問２の問題の記述）
三角形ＡＢＣにおいて
∠Ａ≠０,∠B≠０,∠C≠０,
であり、以下の式１が成り立つときに式２が成り立つように、
式１と式２の係数ｘ、ｙ、ｚ、ｓ、ｔ、ｕの値を定めよ。
（解答開始）
先ず、式２を、正弦定理を使って、上の式３に変換します。
次に、式１を以下のようにベクトルの内積であらわします。
以下の式５と式６である。
は０にはならない。
そのため、式７から、式８が得られる。
（式４から、式３の形の解を得るための条件の全てが式５と式６であるとまでは証明しなかったため、これ以外の解がある可能性が排除できていない。特に、式５と式６が成り立っていなくても、式３の係数を適切に選べば（ただし、その係数は角度Ａ，Ｂ，Ｃに応じて変わるだろうが）式３はいつでも成り立たせることができると言える。）
（解答おわり）
（補足）
この問題２を解いた結果、式１の形の条件から必ず式２の形の式が導けるわけでは無いことがわかった。式１から式２が得られる場合は、式５と式６と式９～式１２が成り立つ場合に限られることがわかった。
一般的な形の式１を式２の形に変換する公式は無い。
よって、問題１において、式１から式２が得られることの証明方法は、それぞれの式を単純化して比較する分析の結果、両式が偶然に一致していることを確認する、上記の解き方で良いことがわかった。
リンク：
別解
複素数平面を使った解答
高校数学の目次
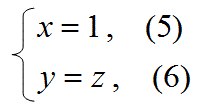
0 件のコメント:
コメントを投稿