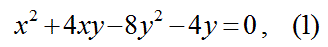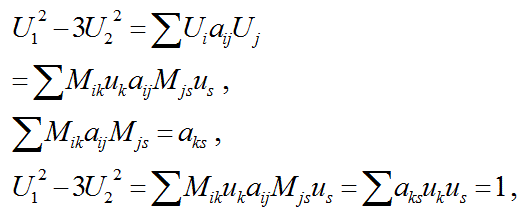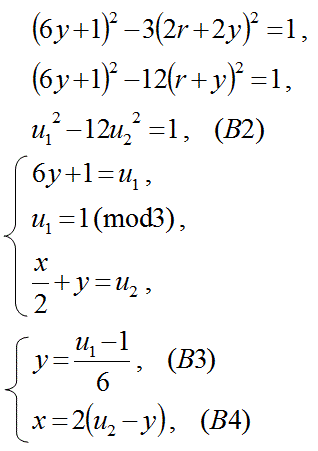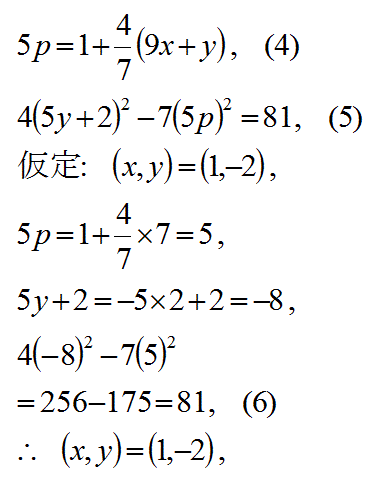【問】(高校生の難問)
(コメント)この問題は、ペル方程式で解けます。
大学入試問題に出題されることもあるようですが、
高校生には難問ですので、理系難関大学や医学部を受験しようとしている高校3年生以外は、この問題をやらなくても良いと思います。
該当する高校生であっても、参考に見ておくだけで十分と思います。
【解1】
解のいくつかを求める。
もう1つの解を計算する。
この場合はx,yは自然数解を持たない。
もう1つの解を計算する。
これは自然数解を持つ。
次に、1つの解を得た場合に他の解を求める漸化式を作る。
作成する漸化式は、以下の式を満たす漸化式にします。
1つの解uが得られた場合に他の解Uを与える漸化式8を、行列Mを使った式で定義します。
式3を扱い易くするために、式3の係数を以下の行列の要素aで定義します。
以下のようにして、行列Mの要素の満たす式を求める。
この式の左右の項の行列を計算する。
この式を満たす行列は以下の式で与えられる。cとdは選択の自由度を与える未知数である。
この式を満足するcとdの整数解を1つ、以下の様に求め、それを使って、行列Mを定める。
これで、1つの漸化式の行列Mが得られた。
ペル方程式の場合は、この漸化式だけで全ての解を計算できることが分かっている。
すなわち、ペル方程式では、c+d√3の値を最小にする自然数解(c,d)=(2,1)を使って上の漸化式を作れば、その漸化式で作った解が全ての自然数解をあらわす。
(漸化式の他の導出方法)
以下のようにこの漸化式を導出する方が簡単なようです。
この漸化式を使って、解を順次に計算できるが、以下では、その計算を先回りして解をあらわす式を求める。
この式を変形して、係数zとmとを使った以下の形の式に変形する。

この式を解いてzとmを定める。

zとmが2組あることで以下の式が成り立つことを利用して解を計算する。

以下のようにk番目の解を計算する。

(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
((U1,k ,U2,k)の式を導き出す簡単な計算方法)
以下の様にすると簡単に計算できます。
(漸化式の他の導出方法)の計算を続けて、以下の計算をします。
(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
(解答おわり)
【解2】
解2では、解1によって計算するx,yの解には整数解以外の解が混在していたのを改善する。
この式B1を式2に代入する。
ここで、u1とu2には正負の何れかであるかが決まっていない自由度がある。
6y+1=1(mod3)であるので、u1=1(mod3)であるu1=か、-u1=1(mod3)である-u1を6y+1に等しいと計算する。
(後の計算で、 常に正のu1=1(mod3)であることが分かる)

この式から、以下の漸化式が得られる。
この漸化式に従うと、
順次に計算する正のu1は常に、u1=1(mod3)となることが分かる。
そのためyの整数解は、B3’のみで計算しなければならない。
一方でxの整数解は、正負のu2を使って、いずれの計算でも整数解が得られる。
この漸化式を使って、(x,y)の整数解をいくつか求めてみる。
これらの計算において、計算した(x,y)は全て整数解になったので、整数解以外の解の混在を無くすことができたと考えられる。
次に、漸化式の計算を繰り返す手順を飛び越えて、一般解をあらわす式を求める。
この一般解の式のx,yには、整数解以外の解が混在していないと考える。
リンク:
高校数学の目次
(コメント)この問題は、ペル方程式で解けます。
大学入試問題に出題されることもあるようですが、
高校生には難問ですので、理系難関大学や医学部を受験しようとしている高校3年生以外は、この問題をやらなくても良いと思います。
該当する高校生であっても、参考に見ておくだけで十分と思います。
【解1】
もう1つの解を計算する。
これは自然数解を持つ。
次に、1つの解を得た場合に他の解を求める漸化式を作る。
作成する漸化式は、以下の式を満たす漸化式にします。
1つの解uが得られた場合に他の解Uを与える漸化式8を、行列Mを使った式で定義します。
式3を扱い易くするために、式3の係数を以下の行列の要素aで定義します。
以下のようにして、行列Mの要素の満たす式を求める。
この式を満たす行列は以下の式で与えられる。cとdは選択の自由度を与える未知数である。
この式を満足するcとdの整数解を1つ、以下の様に求め、それを使って、行列Mを定める。
ペル方程式の場合は、この漸化式だけで全ての解を計算できることが分かっている。
すなわち、ペル方程式では、c+d√3の値を最小にする自然数解(c,d)=(2,1)を使って上の漸化式を作れば、その漸化式で作った解が全ての自然数解をあらわす。
(漸化式の他の導出方法)
以下のようにこの漸化式を導出する方が簡単なようです。
この漸化式を使って、解を順次に計算できるが、以下では、その計算を先回りして解をあらわす式を求める。
この式を変形して、係数zとmとを使った以下の形の式に変形する。

この式を解いてzとmを定める。

zとmが2組あることで以下の式が成り立つことを利用して解を計算する。

以下のようにk番目の解を計算する。

(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
((U1,k ,U2,k)の式を導き出す簡単な計算方法)
以下の様にすると簡単に計算できます。
(漸化式の他の導出方法)の計算を続けて、以下の計算をします。
(注意)この解のx,yには、整数解以外の解が混在しているので、
解を選別して整数解だけを抽出する必要がある。
(解答おわり)
【解2】
解2では、解1によって計算するx,yの解には整数解以外の解が混在していたのを改善する。
この式B1を式2に代入する。
ここで、u1とu2には正負の何れかであるかが決まっていない自由度がある。
6y+1=1(mod3)であるので、u1=1(mod3)であるu1=か、-u1=1(mod3)である-u1を6y+1に等しいと計算する。
(後の計算で、 常に正のu1=1(mod3)であることが分かる)

この式から、以下の漸化式が得られる。
この漸化式に従うと、
順次に計算する正のu1は常に、u1=1(mod3)となることが分かる。
そのためyの整数解は、B3’のみで計算しなければならない。
一方でxの整数解は、正負のu2を使って、いずれの計算でも整数解が得られる。
この漸化式を使って、(x,y)の整数解をいくつか求めてみる。
これらの計算において、計算した(x,y)は全て整数解になったので、整数解以外の解の混在を無くすことができたと考えられる。
次に、漸化式の計算を繰り返す手順を飛び越えて、一般解をあらわす式を求める。
この一般解の式のx,yには、整数解以外の解が混在していないと考える。
リンク:
高校数学の目次