

「微分・積分」の勉強
(6)積分の知識:
「置換積分法」
(ページ内リンク)
▽置換積分の公式の定義
▽公式の第1の証明
▽公式の第2の証明
▽逆向きの置換積分の公式
▽(別ページ)被積分関数を0で割り算して良いのか?
▽(別ページ)広義積分
▽媒介する関数g(t)の条件
〇x=g(t)の関数は単調で無くても良い
〇関数t(x)=t が単調な関数では無い置換積分
〇単調で無い関数 g(x)=g で置換積分する例
□定積分を節約
▽望ましい置換積分方法(積分区間を分割する)
▽定積分する積分区間を間違えないコツ
▽(別ページ)広義積分を前提にしたtan(x/2)等の置換積分の計算事例
▽自由に変数変換できる置換積分の事例
〇見通しの良い解き方
▽(別ページ)変換する変数を関数で導入しても良い
▽1つのtの値に対して複数の値を持つ不定積分
▽変数変換の不思議
▽(別ページ)形が違う同じ式
▽置換積分の条件はどこまで緩められるか
高校生用の微分積分の教科書や参考書は不正確で、勉強用に不適切だと思います。高校2年生が微分積分を勉強するのに適切な参考書は、大学1年生向けの参考書:「やさしく学べる微分積分」(石村園子) ¥2000円 が良いと思います。
【置換積分法】
不定積分∫f(x)dx を求めるときに,積分変数を変換して積分する事を置換積分法といいます。
置換積分では、変数の変換に伴い、被積分関数が変更されます。その被積分関数の式の変形計算では、広義積分を用いる必要を生じるなどの、被積分関数の変形のルールを正しく把握する必要があります。また、変数の変換にともない、積分範囲が変更されます。そのため、積分の範囲のルールを正しく把握する必要があります。
そのように、置換積分にともなって、積分のルールが正しく把握されているかが問われます。以下では、そのルールの正確な情報を説明します。
しかしながら、ルールをあまり知らないでも、とにかく置換積分法に慣れて使い始めたい方もいると思います。その方には、ここをクリックした先で分かり易く説明しているサイト等を参考にしてください。そして置換積分法に慣れて心に余裕が出てきたら、このサイトに戻ってきて欲しいと思います。
例えば、以下のパターンの置換積分の第2の定理の適用に慣れてください。

《1つの例》

《もう1つの例》

《更にもう1つの例》

置換積分法は、以下の図の様に、
「積分する微小面積を、変数xでのグラフと変数tのグラフとで同じにして、積分した総面積を同じにする」
ように被積分関数f(x)を被積分関数h(t)に変換するものです。

(置換積分法の第1の定理)
関数f(x)が、変数xのある連結した区間内の全ての実数で定義された、1つながりに連続な関数である場合、
変数xを、微分可能な関数g(t)で、x=g(t)という式で変数tに変換すると、

が成り立つ。
(置換積分の第1の定理おわり)
(置換積分法の第2の定理=逆向きの定理)
置換積分法には、以下の、逆向きの置換積分の定理があります。
「生き抜くための高校数学」(芳沢光雄) の417ページに逆向きの置換積分の使い方の説明があります。
xで微分可能な関数s(x)でs=s(x)とした変数sを使った置換積分によって、以下のように変数xを変数sに変換して積分できます。

この、置換積分の第2の定理では、dx部分をdsに置き換えるのと同時に、f(x)部分をp(x)に置き換える際にf(x)をs'(x)で割り算してp(x)にしている。
あるx=aの点でs'(a)=0となる場合、そのx=aの点で、式を0で割り算する計算をしているので、これは、式の同値変形では無い。
しかし、被積分関数の分母にs'(a)=0という関数があっても、広義積分によって、積分した結果の関数が、x=aで極限値を持てば、その極限値をx=aでの積分の値であると定義できる。
そのため、s'(a)=0となる関数が分母に来て、積分の定義域からx=aとなる点が除外されても、広義積分によって、x=aでの関数の極限値が存在すれば、x=aの点を定義域に復活できる。また、その極限値が存在しないならば、x=aとなる点で関数が定義され無いことがそのままで正しいのです。そのため、s'(a)=0となる関数s'(x)が分母に来ても良いのです。
(置換積分の第2の定理おわり)
この置換積分の定理(置換積分の公式)は、以下の図の様に、
「積分する微小面積を、変数xでのグラフと変数tのグラフとで同じにすれば、積分した総面積も同じになる」
事を表した定理です。

(必要条件)ΔxもΔtも f(x)Δx=h(t)Δt も微小量であること。
また、微小面積が0になる場合までは考えていない。
それは当たり前で、無条件に成り立つ事のように思えるので、それが成り立つための条件を付ける事自体が余分でおかしな事の様に思えます。
しかし、無条件に成り立つわけではなく、
ΔxもΔtもf(x)Δx=h(t)Δt も微小量であることという必要条件が必ず成り立たなければなりません。
また、微小面積が0になる場合は、対象外です。
公式に付けた条件の、x=g(t)が微分可能であるという条件は、ΔxもΔtも微小量であるために必要な条件を数学的に記述したものです。
また、g(t)が微分可能であるという条件が満足できない場合には、変数xの区間を、公式の条件が完全に満たされる狭められた区間に分割し、その分割した区間毎に置換積分を行なう。それで得た複数の区間毎の不定積分を、分割した区間の端でつないで1つながりに連結した不定積分に拡張する。そうすれば、g(t)が微分可能で無い点で区間を分割して不定積分し、後で各区間の不定積分をつなげば良いので、公式の条件が満足できない場合にも対応できます。
【第1の定理の第1の証明】
(1)先ず、xを媒介変数 t であらわす関数g(t)は、tが変化したときにどのくらい変化するか調べる。
そのため、x=g(t)をtで微分する。

x=g(t)がtで微分可能、すなわち、(Δx/Δt)が有限の値ならば、
Δxが以下の式であらわされる。
(2)その場合に、以下の式が成り立つ。
以上の計算で、g'(t)の値が確定した有限の値でありさえすれば、たとえ、g'(t)が不連続な関数になってもかまわない。
(証明おわり)
【第1の定理の第2の証明】
置換積分法は、合成関数の微分の公式の同類です。
(証明開始)
先ず、
とすると,
である。
そこで
とおき,
を考えると,g(t)が微分可能であれば、
合成関数の微分の公式によって、
となる。
(合成関数の微分の公式はここをクリックした先を参照)
そして、その様にその関数 f(g(t))g'(t) の値が有限の範囲内にあれば、以下の式の左辺の積分が可能である。
(もしg'(t)が連続関数であれば、関数 f(g(t))g'(t) は連続関数になるので微分積分学の基本定理の条件が満足され、以下の式の左辺の積分が確実に可能である)

となります。
(証明おわり)
【第2の定理=逆向きの置換積分の定理】
置換積分の公式の概念は:

(必要条件)ΔxもΔtも f(x)Δx=h(t)Δt も微小量であること。
また、微小面積が0になる場合までは考えていない。
という概念に基づく公式でした。
微小面積が0になる場合を全く考慮せずに、
という条件に限定すると、
dx/dt≠0,
dt/dx≠0,
となってしまうので、
公式の制約が大きいです。
(場合1)dx/dt=0の場合
しかし、先に証明できた置換積分の第1の定理は、
dx/dt=0
の場合に適用できます。

とすると:
dx/dt=0
の場合にも使える第1の定理:
すなわち、
の場合に:
となる場合に、

を積分範囲に含んで、

が成り立つという置換積分の第1の定理が使えます。
(場合2)dt/dx=0の場合
dt/dx=0
の場合には、
x=g(t)の逆関数の

を使う第2の定理を使います。

すなわち、
の場合に、
となる場合に、
を積分範囲に含んで、

が成り立つので、この式を逆さにした、

という形の式の第2の定理=逆向きの置換積分の定理を使います。
しかし、このように式を逆向きにして使って良いとする論理には欠陥があります。
置換積分の第1の定理ならば、式h(t)が定義されていて、かつ、s'(x)が定義されているならば、変数tで積分する被積分関数h(t)を、変数xで積分する被積分関数f(x)に変換できます。この場合は、h(t)が定義されていれば、必ずf(x)が定義されます。しかし、第2の定理では、式f(x)が定義されているならば、必ず式h(t)が定義されるという保証は有りません。そのため、そのまま、第1の定理の式を逆にして、h(t)=f(x)/s'(x)=p(x)=h(t)を被積分関数にした積分を正当化する事には論理の欠陥があります。しかしながら、広義積分を適用することで、s'(x)=0の場合を無視して良くし、また、h(t)が定義されなくても積分を可能にしているのです。
(補足)---------
第2の定理の式は、置換積分する中間の式に、
dtとなる、dt=s'(x)dx
が出て来る式です。
置換積分の第1の定理では、
置換積分する中間の式に、
dxとなる、dx=g'(t)dt
が出て来ていました。
置換積分の第1の定理と第2の定理(=逆向きの置換積分)は、
xの関数s'(x)とdxをまとめたs'(x)dxを、ds(x)=dtに置き換えて考える(第2の定理)か、
dx=dg(t)を、tの関数g'(t)を使ったg'(t)dtに置き換える(第1の定理)か、だけの違いです。
s'(x)=1/g'(t)
であり、((dt/dx)=1/(dx/dt)とも表現できます)
g'(t)=1/s'(x)
です。((dx/dt)=1/(dt/dx)とも表現できます)
dx/dt=g'(t)が無限大になった場合に第1の定理は使えないのですが、s'(x)=0は存在するので、s'(x)を使った第2の定理を使って計算をする事が多いですが、それはごまかしです。第2の定理でも、「被積分関数を割り算する関数s'(x)が0でない」という、第1の定理での、g'(x)が存在するべき制約条件に対応する制約条件が必要だからです。しかし、広義積分を適用することで、被積分関数を割り算する関数s'(x)が0になっても問題無く積分できるようにしています。
(補足おわり)------------
例えば、
以下の積分を考えます。
ここで、以下の様に変数xを関数g(t)を使って変数tに変換する事を考えます。
この場合に、関数x=g(t)のグラフは下図のようになります。
t=1のとき、
g'(t)が無限大になり、有限の微分係数g'(x)=dx/dtが存在しないので、第1の定理が使えません。
その場合には、関数x=g(t)の逆関数t=s(x)を考えて、その関数s(x)の微分s'(x)=dt/dxを考えて、
関数s(x)を使うのであれば、微分係数dt/dx=s'(x)の値が有限の値になるので第2の定理を使う事が多いです。cos(x)=dt/dx=s'(x)としてcos(x)を置き換える以下の計算が行われています。
このようにして、逆向きの置換積分により、g(t)の逆関数t=s(x)を使って変数xを変数tに置換積分する積分ができたように見えます。しかし、この逆向きの置換積分の計算には、厳密には、s'(x)≠0という制限条件が必要です。しかし、広義積分を適用することで、s'(x)≠0という制限条件を無視しても良いのです。
リンク(別ページ)被積分関数を0で割り算して良いのか?
リンク(別ページ)広義積分
【媒介する関数g(t)の条件】
《g(t)が微分可能という公式の条件の意味》
置換積分の公式の前提条件にある、g(t)が微分可能であるという条件の意味は、第1の証明で使ったΔxを以下の式であらわすため。
そのために導関数g'(t)が存在する事が必要でした。
導関数g'(t)が存在しない点がある場合は、媒介関数g(t)の逆関数s(x)を考えて、
という変換を考える逆向きの置換積分の公式(第2の公式)を使って、
s'(x)dx=dt
という置き換えをしてxによる積分の式をtによる積分の式に変換してg'(t)が存在しない問題を回避します。それにより問題が回避できる根拠は広義積分によります。
積分区間の点で、導関数g'(t)が存在しない場合に、その点を除いて分割した積分区間で積分が可能です。そして、広義積分を用いて、g'(t)が存在しない点での積分の値を定め、その点で、分割した積分区間をつなぐことで、g'(t)が存在しなかった点を含む領域にわたる置換積分が可能です。
分割した積分区間の端点でg(t)は微分可能で無くてg'(ta)やg'(tb)が存在し無くても分割した積分区間の中でg(t)が微分可能であれば積分が可能です。
(広義積分の解答を書く場合には、良く説明する必要があります。ただし、高校数学では広義積分は扱わない。)
《変数gの定義式x=h(g)の関数の一部を切り出して使う事例》
以下の様に、変数xでの関数f(x)の積分を、変数xの定義域のうち、x≧0の部分を変数gのg≧0の定義域に対応させて、変数xを変数gに置き換えて置換積分する場合を考えます。
定義域がg≧0である変数gを媒介変数にして置換積分する場合は、先ずは、x≧0の区間内でのみ関数f(x)が置換積分できる。
(事例おわり)
この置換積分では、x≧0の区間内でのみ定義された不定積分の解が得られた。
(置換積分の条件が合っているか)
置換積分の条件は、
(1)ある連結区間[a,b]でf(x)が連続な関数である。
(2)その区間[a,b]内の全てのxの値をx=g(t)と表し、
g(ta)=a,g(tb)=bとなる関数g(t)が、
連結区間[ta,tb]又は連結区間[tb,ta]で微分可能である。
(3)その連結区間[ta,tb]又は連結区間[tb,ta]で、関数g(t)の値が、連結区間[a,b]から、はみ出さないものとする。
この事例では、x≧0の区間という狭められた区間[a,b]で、上記の置換積分の条件が成り立っている。上記の置換積分の条件の意味する事は、そういう条件を満足する区間に、関数f(x)及びh(g)の定義域を狭めて置換積分を行うという事を意味する。
(事例の続き)
この事例の置換積分では、関数f(x)のx<0の区間での不定積分はできていない。x<0の区間の不定積分は、以下の様に行なうことができる。すなわち、定義域がu<0である変数uをx<0の変数xに対応させる置換積分をすることができる。
そして、定義域がu<0である変数uを媒介変数にして、x<0の区間内で関数f(x)が置換積分できる。
(事例の続きのおわり)
この置換積分では、x<0の区間内で不定積分の解が得られた。
以上の媒介変数uによる式と媒介変数gによる式を合わせると、変数xの全領域での不定積分の式が得られた。
置換積分の関数の条件は、関数を積分する変数の連結区間[a,b]内での条件であり、その条件は連結区間を狭くすれば満足できるようになると認識するべき。
また、置換積分を考え易くするために、更に以下の関数の条件を加えても良い。
すなわち、連結区間[a,b]での関数f(x)の積分を媒介する関数x=h(g)は、単調増加関数か単調減少関数であるものとする。この条件の関数h(g)を用いて置換積分することが望ましいと考える。
そういう関数h(g)=xを用いる条件は、置換積分の区間[a,b]を細分化するだけで実現できる。その各区間[a,b]毎に、関数f(x)の積分を媒介する関数h(g)=xを定義して使えば良い。そうすれば、その関数h(g)の逆関数が存在する。それにより置換積分が行ない易くなるので、それが望ましい。
単調な関数を使って変数 x を変数 g に変換するという事は、変数 x と変数 g を1対1対応させることを意味する。そのように、変数同士を1対1対応させている条件の下では、等式の左右の項を各々2乗した等式を作る式変形は同値変形である。出来上がった等式は元の等式と等価な式である。そのように、多くの式変形が同値変形になるという便利さがある。
《x=g(t)の関数は単調で無くても良い》
第1(及び第2)の証明において、例えば、下の図の様に、g(t)が、a=g(ta)となるt=taから始めて、tとともに増加するが、g(tb)=bに達する前に、一旦減少して、再び増加して、g(tb)=bに達する関数であっても、この証明が成り立っている事に注意する事。
そういう関数g(t)を使って置換積分しても良いのです。

また、置換積分するf(x)の積分変数xの定義域を、ある連結区間[a,b]に狭くできれば、用いる関数g(t)は、その区間内のxを表す事ができるだけでも良い。その関数g(t)が、その連結区間の外のxの値を表す事ができなくても良いのです。
《関数t=t(x)が単調な関数では無い置換積分の例》
変数xでの関数f(x)の積分を、以下の様な、単調では無い関数t(x)であらわされる変数t=t(x)で置換積分することもできる。

この場合には、この関数t(x)を、図の点Mで2つの関数に分割して、それぞれの関数毎に置換積分する。
以下の積分を、以下のパターンの第2の置換積分の公式を使って置換積分する。

以下の積分を計算する:
先ずは、x≧0を定義域とする関数t(x)で置換積分する。

次に、x≦0を定義域とする関数t(x)で置換積分する。

この2つの置換積分を合成した置換積分にする。その際に式(3)と式(5)を省略して計算ができる。そして、その、省略できる式(3)と式(5)以外の式は同じ式なので、式(3)と式(5)以外の式だけを使って、2つの置換積分を1つにまとめた計算式で置換積分しても良い。
(事例おわり)
《関数g=g(x)が単調な関数では無い置換積分の例》
以下の様に、変数xでの関数f(x)の積分を、媒介変数g=g(x)を使って、第2の置換積分の公式で置換積分する事例を考える。
見通しの良い解答のためには、変数xの定義域を分割した区間毎に単調な変数変換の関数を用いて積分することが望ましい。そのため、以下の様に、変数xの区間毎に、変数変換の単調な関数h(g)=xとp(g)=xを定義して解く。

先ず、一旦は、以上の式2と式3で、変数xの定義域を分割した区間毎に、積分を媒介する単調な関数h(g)とp(g)を定義する。それらの関数は、逆関数が存在するので、積分の見通しが良くなるので嬉しい。
次に、式1を微分して式4を導き、以下の様に計算する。
(解答おわり)
この解は、式2と式3が計算に代入されず無駄にあるように見えますが、式2と式3は、変数xと変数gの対応関係を明確にしたという意味を持つので、必要な式です。
(単調で無い関数 g で置換積分し定積分の計算を節約)
ちなみに、この不定積分を使って、
x=−1からx=1まで、xの関数の定積分を求めると、
1の2乗−(−1)の2乗=0
になります。
それに対応する、
(x=−1から0)g=1から0まで
(x=0から1)g=0から1まで
のgの関数の定積分は、
それぞれの区間でgの関数の定積分の和を求め、
総体の定積分の結果は0
になります。
この場合は、以下の様に、媒介変数gを用いた積分の被積分関数は、g=1から0までの積分区間でも、g=0から1までの積分区間でも、同じgの関数になる。そのため、その被積分関数を積分の起点のg=1から積分の終点のg=1までの積分としても良い。
(解答開始)
(解答おわり)
しかし、媒介変数gによる積分区間が1~1のように見えるのはみせかけにすぎず、この積分の正しい区間は、
1→0→1
です。
この区間内に積分が不可能な点(例えば無限大に発散する点)が含まれている場合は、この積分はできません。
その正しい積分区間
1→0→1
で、関数が異常になる点が無いかどうかを点検した上で、積分区間を
1→1
に節約して積分ができるのです。
(定積分の計算の節約の説明おわり)
(補足)
この問題の置換積分を逆にして、変数gによる積分を、第1の置換積分の公式を使ってg=g(x)として、変数xによる積分に変換する置換積分を考える。すなわち、以下の計算を考えます。
第1の置換積分の公式の証明では、関数g=g(x)が単調増加な関数で無くても公式が成り立っています。そのため、以上の計算には全く問題がありません。このように、単調では無い関数g=g(x)を使って置換積分しても良いのです。
(補足おわり)
このように、置換積分の公式は、第1の置換積分の公式と合わせて、第2の置換積分の公式も使え、双方向の変数変換の置換積分の公式が使えます。単調な関数h(g)の逆関数s(x)を使って、式を逆向きに置換積分する第2の置換積分を考えると、積分の過程が明確になって理解し易くなります。媒介関数h(g)の微分可能性が妨げになっても、その逆関数の媒介関数s(x)の微分可能性は妨げにならなければ、妨げが少ない関数を使って第2の置換積分をします。(しかし、その妨げが避けられている本当の理由は、広義積分をしているからです)
《導関数g'(t)は連続で無くても良い》

参考書によっては、導関数g'(t)も連続な関数である(「連続微分可能」とも言う)場合を、置換積分の公式が成り立つ条件としている参考書もあります。しかし、その条件が無くても公式は成り立ちます。以下で、その理由を説明します。
「関数g(t) を微分した導関数g'(t)も連続な関数である」
という条件が加えられる理由は、
導関数g'(t)が連続な関数であれば、それと何か連続な関数との積も連続関数になり、連続な関数は積分可能だから、置換積分の公式を証明し易くするために設定された条件でした。
しかし、連続な関数で無くても積分可能な関数はあります。g(x)のある点で微分が出来なくても、その点でg'(x)が発散しない限り、g'(x)は、その点も含んだ積分区間で積分が可能です。
また、第1の証明の中での前提条件は、g'(x)が有限の値である事であって、g'(x)が連続である事は証明には必要ありませんでした。
そのため、この条件は、本来は必要ない。(この条件は、置換積分を把握し易く考え易いようにするために加えられた条件です。この条件を守って置換積分するならば、計算の見通しが良くなり計算ミスを防ぐ事ができます。)
「本来は、g(x)が微分可能で、g'(x)が存在する」という条件だけで充分と考えます。
「微分可能関数の導関数は、中間値の定理も満たすので連続関数に極めて近い関数ではないか」
(微分可能な関数g(x)の導関数g'(x)が不連続な例)
g(x)を以下で定義する原始関数F(x)とし、
g'(x)=f(x)とすると、
f(x)=g'(x)は、
F(x)=g(x)の微分で作られたので、積分可能です。
(F(x)=g(x)の定義)
x≠0の場合:
x=0の場合: F(0)=0,
(導関数f(x)=g'(x))
原始関数F(x)=g(x)はx≠0の場合も、x=0の場合も、微分可能で、
その導関数f(x)=g'(x)は、以下の式であらわせます。
x≠0の場合の微分:
になり、xが0に近づくと-1と1の間を振動します。
この導関数が含むcos(1/x)の関数が以下のグラフであらわす形の関数になるからです。
X=0の場合にも、F(x)は微分可能で:
というように、0になります。
このように、x=0の場合の導関数f(x)=g'(x)は、x=0で不連続ではありますが、f(0)=0という値を持ちます。
この導関数f(x)=g'(x)は、x=0で不連続ですが、x=0で関数値を持ち、積分すると原始関数F(x)=g(x)になる、積分可能な関数です。
しかも、その積分結果の原始関数F(x)=g(x)を微分すると、元の、x=0で不連続な関数f(x)=g'(x)が得られます。
この様な関数g(x)を使って置換積分をした場合、関数g'(x)は細かく振動しますが、関数値が無限大に発散する事が無く有限な値を持つ積分可能な関数です。
g'(x)は積分可能なので、それを含む置換積分の公式も成り立ちます。
そのため、
そういう事からも、置換積分の公式の条件は、「g(x)が微分可能で、g'(x)が存在する」という条件だけで充分のように考えます。
《関数g(t)は完全に微分可能で無くても良い》
「関数g(t)が微分可能な関数である」条件は、広義積分においては、変数tの定義域内の疎らな点で関数g(t)が微分可能で無くても、それ以外の区間でg(t)が微分可能であれば置換積分が成り立ちます。
その事を以下で説明します。
合成関数の微分の公式が成り立つので、置換積分の公式が成り立ちました。
しかし、合成関数の微分の公式が成り立たない場合にも置換積分の公式が成り立つ事がある事に注意する必要があると考えます。
ある1点tにおいて、
例えば、g(t)が微分可能では無くて、合成関数の微分の公式:
が成り立たない点があった場合。
その点を除外した、その点の両側の連結区間で、各々積分ができます。
そして、その積分の後で、その1点tの両側の積分区間での積分結果の関数を1つながりに連結する事もできる。そういう操作(広義積分)で得た関数では、
が成り立ちます。
すなわち、被積分関数の積分変数xの連結区間[a,b]の中に、合成関数の微分の公式が成り立たない1点が含まれていても、広義積分の不定積分では、置換積分の公式が成り立つ事があります。
この点で、広義積分における、置換積分の公式は、合成関数の微分の公式とは異なります。
g(x)が微分可能ということは、広義積分においては、積分区間の全域で完全に成り立っていなくても良いのです。
【不定積分の区間は開区間(a,b)にもできる】
不定積分の置換積分の公式は、積分範囲を、区間の端を含めない開区間(a,b)にしても成り立つ。
定理3.4 (置換積分法)
ある連結開区間(a,b)でf(x)が連続な関数である場合
(その場合は、その開区間の端ではf(x)及びその不定積分が無限大に発散する事があり得るが、(a,b)に含まれる閉区間での定積分は無限大にはならない)、
変数x=g(t)とおくと、g(t)が微分可能であれば、

が成り立つ.
(公式の定義おわり)
この様に、不定積分の区間を連結する開区間(a,b)にする場合は、g(t)の微分可能性の条件も、区間の端を考えないで良いので単純に開区間(ta,tb)又は(tb,ta)で微分可能であるだけで良くなり、分かり易くなる。
ここで、開区間(a,b)で関数f(x)の不定積分を求めた場合、その不定積分が定義される開区間(a,b)をはみ出した区間で定積分してはいけません。例えば、区間の端点を含めた閉区間[a,b]で定積分してはいけません。
また、媒介関数g(t)が微分可能で無く置換積分の条件が成り立たない場合に先ず行う事は、
逆向きの置換積分を行うと良いと考えます。
すなわち、媒介関数g(t)の逆関数s(x)を考えて、
という変換を使う逆向きの置換積分の公式を使って、以下の式の形の公式を使って積分変数を変換すれば良いのです。
この式で、
s'(x)dx=dt
という置き換えによって、
dxをdtに変換すれば良いのです。
このようにして、媒介関数g(t)=x がtで微分可能でなかった問題を回避します。(ただし、先に説明したように、s(x)を使う逆向きの置換積分の計算によっても、g(t)が微分可能で無かった問題は解消していません。広義積分の概念によってこの問題が解消するのです。)
(定積分の置換積分の公式について)
また、定積分の積分区間は、必ず端がある閉区間[c,d]です。そのため、定積分の置換積分の公式は、積分区間が閉区間に限定された場合の公式になります。その点で、定積分の置換積分の公式は、不定積分の置換積分の公式と違ってきます。
【望ましい置換積分方法】《積分区間を分割する》
置換積分の変数xを変数tに変換する関数g(t)=x に単調な関数を用いるという条件が大切です。その条件を緩めても置換積分が可能な場合がありますが、関数g(x)に単調で無い関数を用いる事は望ましく無い。
なぜならば、単調な関数には逆関数が存在するので、積分の計算の見通しが良くなる利点があるからです。
(積分区間を分割して、それぞれで積分する)
媒介関数g(t)=xを単調な関数にするには、変数xの定義域を、関数g(t)が単調になる区間毎に分割する。その区間毎にg(t)が単調な関数になるので、各区間で、g(t)の逆関数が存在する。その区間毎に不定積分を求め、それらの不定積分を連結して1つながりに連続な不定積分を求める広義積分を行なえば良い。それにより、関数g(t)を単調で無い関数(逆関数が存在しない)にした場合と同じ積分ができる。そのため、変数xの定義域を、関数g(t)が単調な関数になる区間に分割して、見通しの良い計算をする事が望ましいのです。

(1)
考え易い関数を使って置換積分の条件を単純化するために、以下の関数を使うことが望ましい。
すなわち、積分を媒介する関数x=g(t)は、1つながりに連続であって、単調増加関数か単調減少関数であるものとする。
単調増加関数か単調減少関数には必ず逆関数が存在するので、逆関数の概念も使って積分の計算が進められ計算の自由度がとても大きくなる効果があります。
(2)
もし、媒介関数g(t)=xがある積分区間で単調な関数で無ければ、g(t)=xが単調である区間に積分区間を分割する。そうすれば、その分割された積分区間でg(t)=xが単調な関数になる。その各区間毎に置換積分すれば良いのです。
x=g(t)は、すなわち、媒介変数tによる関数g(t)の値は、変数xの全部の範囲をカバーしないで良いのです。被積分関数が変数xによって定められる変数xの全区間の一部の区間をカバーするだけで良いのです。
(3)
区間[a,b]に限って置換積分して不定積分を求める。その区間[a,b]に隣接する区間[c,d]で置換積分して不定積分を求める。それらの不定積分の関数同士が、閉区間が隣接する境界の極限で1つながりに連続に連結できるかを考える。
すなわち、不定積分の部分として、確実に置換積分可能に範囲を狭めた連結区間[a,b]や連結区間[c,d]での不定積分の部分を複数求め、その関数を連続につないで1つながりに連続した不定積分を作るという広義積分を行なえば良いのです。
(「積分可能の定義」のページで説明した、部分部分の関数の接続方法と同じです。)

その1つながりに連続した解の関数は、置換積分可能な媒介関数g(t)の制限を可能な限り緩めて置換積分して得た不定積分の解と同じです。
(4)
その様に、後で不定積分の部分を連結する事を前提にして、以下の様に、置換積分する関数の条件が満足される(分割された)連結区間[a,b]を求める。
(A)関数f(x)の、ある連結区間[a,b]で連続な部分を考え、
(B)また、その連結区間[a,b]内の全てのxの値をx=g(t)と表す、g(ta)=a,g(tb)=bとなる1つながりに連続な関数で、
tの区間の端を除いた連結区間(ta,tb)又は連結区間(tb,ta)の点でtで微分可能な関数g(t)を考える。
(C)また、関数g(t)の値が、変数tの連結区間[ta,tb]又は連結区間[tb,ta]で、単調増加か単調減少であるように、tの連結区間[ta,tb]又は連結区間[tb,ta]とxの連結区間[a,b]を定める。
(D)g(t) をtで微分した導関数g'(t)も連続な関数となる(連続微分可能)関数g(t)を使う。
(E)それらの条件が成り立つxの連結区間[a,b]とtの連結区間内で定義される不定積分:

を求める。
(5)
そうして、xの連結区間[a,b]毎に別々にf(x)の不定積分を計算する。そして、それらのf(x)の不定積分の各連結区間[a,b]の境界で不定積分が極限で連結されると、1つながりに連続な関数に連結できるかを考える。その1つながりに連続する関数を、広義積分における、置換積分された不定積分の関数とする。
このようにして、見通しの良い関数を使って置換積分する事が望ましいと考えます。
【定積分する積分区間を間違えないコツ】
後で説明する、置換積分を媒介する関数g(t)の条件を緩められる事の説明の中の事例のように、被積分関数が不連続であっても積分できることがある。
そのため、被積分関数が連続であるか否かという、積分可能の判定条件は、広義積分においては、便宜的な十分条件であって、積分可能のための必要条件ではありません。
広義積分における置換積分の公式の必要十分条件(積分可能の条件)は、積分可能の定義のページで説明した様に、
不連続な関数f(x)に対しても、
その定義域を、関数f(x)の連続で無い点を除外した連結区間に分割し、
それら各連結区間毎に不定積分を計算し、
得られた各不定積分を連続につないで1つながりに連続な不定積分を構成します。
その不定積分を使って
F(b)-F(a)
の式で定積分を計算して良いのです。
この、
「積分結果の不定積分の関数F(x)が積分区間[a,b]で1つながりに連続する」
という条件が、
拡張した置換積分の公式においても、公式が成立する区間[a,b]を定めるための必要十分条件であると考えます。
(もう1つの注意点)
不定積分する積分区間は、
f(x)を積分する積分変数xが積分区間内を動くとき、
被積分関数f(g(t))g'(t)を積分する積分変数tが、どの点からどの点まで動くかを調べる事が必要です。
その積分範囲は、
被積分関数f(g(t))g'(t)を変数tで不定積分して得た関数H(t)が連続で無い点をまたぐ範囲ではないハズです。
関数H(t)が連続で無い点をまたいだ範囲を積分範囲と考えてはいけません。
その積分の範囲が、例えば、
t=taからt=∞、
t=-∞から、t=tb
までというように、積分変数tの積分範囲が分断された区間になる場合もあります。
そのように区間が分断されている場合は、
H(∞)-H(ta)==Aと、
H(tb) -H(-∞)=B
とを分けて求めて、
A+Bを求めれば良いのです。
【関数の微分可能性が公式を制約する】
置換積分の公式は、合成関数の微分の公式を使って証明できます。そのため、合成関数の微分の公式の同類です。
また、それ以外の同様な式で表された式を含む以下の公式群の同類です。
この各公式には、先ず、以下の縛り(成立条件)があります。
その縛りというのは、
「上の式の様に微小量の割り算であらわした式の、ΔhもΔxもΔtも、何れも微小量でなけばならない」
とういう条件です。
(例題)
例えば、
被積分関数(dh/dx)=f(x)の変数xによる積分を、
媒介変数 t と、
媒介関数g(t) =(1/t)= x
を使って置換積分する場合、
Δx=Δg=Δ(1/t)が、
t→0で、微小量にならないから、
t→0の場合には、関数g(t) =(1/t)= x を媒介関数に使うことができません。
(媒介関数g(t)は、t=0で微分可能で無い)
そして、各関数の微分可能条件を(あたりまえの条件のように見えますが)意識する必要がある事に気をつけてください。
「関数が微分可能(有限の値の確定した値の微分係数が存在する)」
という意味は、
「関数が、その変数のその値に限って、その変数で微分可能であれば良く、その変数のその他の値での関数の微分可能性は関係しない」
という意味です。
広義積分では、後で説明するように、変数 x での積分を、媒介変数 t での積分に変換する置換積分の媒介関数g(t)=x の条件を緩められます。
それを考えると、
置換積分を媒介する関数g(t)=x が、t=0近くで、
「媒介関数g(t)=x が、微分不可能な点の t=0 以外の点では微分可能で、t=0 の点も含めて1つながりに連続である」ことが、
広義積分において、被積分関数h(g(t))g'(t)が媒介変数tで積分可能であるために本質的に必要な条件であると考えます。
例題で、媒介関数g(t) =(1/t)を置換積分に使った場合、t=0では、
「媒介関数g(t)が1つながりに連続である」条件が成り立ちません。
そのため、広義積分においても、
t→0の場合には、関数g(t) =(1/t)を使うことができません。
(積分できない変数xの範囲に気をつける)
下図の関数f(x)は、x=0の点では関数f(x)の値が-∞になり、関数が定義されていないで、関数が不連続です。そして、この関数では、x=0を含んだ範囲で積分することはできません。
上図の関数を、上図の様にx=0を含む区間で定積分したら、マイナスの無限大になるので、積分が不可能です。
そのため、上図の関数を、例えば-1から1までの区間で積分する事も不可能です。
そのため、この関数f(x)の不定積分の変数xの定義域の閉区間は、x=0を含む事ができません。
これを無視して、関数f(x)の不定積分F(x)の変数の定義域にx=0を入れてしまうと以下の間違いをおかします。
F(x)=1/xをxで微分したら
になります。
そして、変数xで積分する区間内に、f(x)が発散する点のx=0を含めた、xが-1から1までの区間で、
関数f(x)の定積分を、F(x)を使って、 F(1)-F(-1)=1-(-1)=2
という 計算で求めると、明らかに間違えます。
上の図で明らかな様に、-1から1までの範囲でのf(x)の積分はf(x)のグラフの面積にならなければなりません。そのため、定積分の答えは、マイナス無限大にならなければなりません。そのため、 F(1)-F(-1)=2は、明らかに間違っています。
こういう間違いを、置換積分の計算でもおかさないために、置換積分の計算において、常に、積分範囲が適切であるかに注意しなければなりません。
以下では、被積分関数f(x)の変数xでの不定積分を媒介変数 t での不定積分に置換積分する場合を考えます。
という計算をして不定積分を求める場合に、
積分可能な範囲が、
x<0,
または、
x>0
である事を認識します。
すなわち、式の変形の過程で出てくる
「微分(dx/dt)や(dt/dx)が微分可能となる積分変数xや積分変数tの連結区間の範囲のみで、積分が可能である」
と考えて、
この不定積分を用いて定積分できる積分可能な範囲がどこからどこまでになるかを、注意深く考えながら、
積分の式の変形をしてください。
例えば、1つながりに連続なf(x)の不定積分を、
1つながりに連続なh(t)を使って、以下の計算で求める。
(第1の積分)
その後に、未だ不定積分をしていない、以下の1つながりに連続なf(x)を、以下の1つながりに連続なh(t)を使って、以下の様に不定積分する。
(第2の積分)
以上の2つの不定積分を同時に行なってはいけません。
第1の積分により、第2の積分も終わっていると考えないようにして下さい。
1度に不定積分できる範囲は、関数f(x)が1つながりに連続な区間内のみだからです。
(悩ましい問題)
置換積分に限らず、1度に不定積分できる範囲は、関数f(x)が1つながりに連続な区間内のみです。
以下の、1つながりに連続な関数f(x)の不定積分を、
以下の様にして不定積分する。
(第1の積分)
その後に、未だ不定積分をしていない、以下の1つながりに連続なf(x)を、以下の様に不定積分する。
(第2の積分)
以上の2つの不定積分を、第1の積分により、第2の積分も終わっていると考えないようにしてきたでしょうか。
1度に不定積分できる関数f(x)は、1つの、1つながりに連続な関数だけです。
しかし、今までの不定積分では、x>0の区間で1つながりに連続な関数と、x<0の区間で1つながりに連続な関数を、区別して別々の不定積分としてこなかったと思います。
(その積分では不定積分のルールが守られていないので、悩ましい問題だと思います。)
しかし、置換積分で自由自在に変数変換をするようになると、少しのルール違反も計算を誤らせる事になります。
そのため、置換積分では、そのルール違反はもはや見逃せなくなっています。
なお、関数が不定積分できた積分変数xの積分区間の判定方法は:
不定積分ができた積分変数xの範囲は、
不定積分の関数が、1つながりに連続な連結区間です。
不定積分が1つながりに連結する積分変数xの区間を1単位にし、
その1単位毎の関数は、異なる不定積分の関数とします。
上の例:
(第1の積分)
(第2の積分)
では、
x<0, での t+C という不定積分と、
x>0, での t+C という不定積分とは、
異なる関数だと言えます。
(不定積分を表す関数の変数tの定義域が異なれば異なる関数だからです)
なお、関数 f(x)が定義される変数xの連結区間からはみ出させた値cの点を経由する変数xの積分区間
(始点aから経由点cを経由して終点bまで至る積分区間)
でf(x)を積分した値は、
終点bでの不定積分F(x)の値と始点aでの不定積分F(x)の値の差 F(b)-F(a) とは異なった値になります。
【自由に変数変換できる置換積分の事例】
(事例1)
以下の不定積分を置換積分で求めてみます。
x≧-1の場合に:
【解答】
積分変数xを以下の積分変数tに変換する。
(解答おわり)
この不定積分は、積分変数を、ここをクリックした先のサイトのように変換して解く事もできます。解を得るための積分変数の変換方法は、その様に、かなりの自由度があります。
(事例1おわり)
【いつ置換積分を考えるべきか】
置換積分とは、積分変数の変換です。積分変数の軽い変換、例えば、x→t+Aや、x→2t等の変換をしたらどうなるかは、常に思考実験する(解答には書かないが)心がけが必要です。
次に、それより重い積分変数の変換、例えば、sinx=t 等を試す。
積分変数の軽い変換は、いつだって(解答に書かないでも)思考実験で試して、良い変換を思いついたら、いつでも使えるようにするべきです。
積分変数の軽い変換(x→t+Aや、x→2t 等)を常に思考実験するのは、積分の式の変形の可能な未来を見通すという事であって、解を考える時にはいつでも必要な事です。
積分変数の重い変換も、その次に頻繁に発想し、その重い変換の結果で式がどう変わるかの、変数の変換の経験を憶えていくと良いと思います。
こういう式になったら、x→2t に変換する、というのでは無く、
思考実験でx→2t に変換したら式がきれいになった時に、x→2t に変換する置換積分の式を解答の式に書くのです。
(小手わざ)
以下の様に変換できるという小手わざを覚えておいて使うと計算が楽になると思います。
この小手わざは体で自然に覚えておいて、分母にsin(β)がある関数をβで積分するときに、体が思い出して、β=2θとして変数を t に変換して使うようにできると便利だと思います。
(事例2)
以下の各事例では、置換積分による積分変数の変換がどこまで自由に変換できるかを考えていきます。
考え易い関数を使って置換積分の条件を単純化し、積分を媒介する関数x=g(t)は、単調増加関数か単調減少関数であると限定して考えて良い。
そういう限定をして、単調増加(又は、単調減少な)関数 f(x)と、その逆関数g(y)を考えます。
この場合、以下の積分を以下の様に置換積分する事ができます。
この様に、yをxの関数とした積分を、xをyの関数とした積分に置き換える置換積分が可能です。
同様にして、以下の積分を以下の様に置換積分する事が可能です。
以上の様に、置換積分法では、変数xと変数yを対等であると考えて、変数を置き換えて置換積分します。
変数yが変数xの関数であるとして変数xで積分していた積分を、変数xが変数yの関数であるとして変数yで積分する積分に置き換えるというダイナミックな変数の切り替えを行うのが置換積分法の特徴です。
このような変数変換を利用すると、ここをクリックしたサイトの逆関数の積分も解けるようになります。
(事例2おわり)
(事例3)
以下の様に、変数xでの関数f(x)の積分を、媒介変数gで置換積分する場合を考えてみます。
(注意)
変数xの正と負の定義域を持つ関数g=g(x)は単調な関数では無いので、逆関数を持たない。しかし、変数xが正の定義域でg(x)であると定義された関数は単調な関数なので逆関数を持ちます。xが負の定義域でg(x)であると定義された関数も、同様です。
この被積分関数を積分変数gのみで表そうとすると、以下の2つの場合に分かれます。
第1の場合:
もう1つの場合:
この様に、置換積分の結果が、積分変数xの2つの区間で別れた、異なる積分変数gの式であらわされる、xの定義域が異なる2つの関数になった。
そのため、この解の不定積分を使って定積分する場合は、以下の様に計算します。
(事例3おわり)
この事例3は、解の見通しが良くなかったと思います。見通しの良い解にするには、以下の様に、直接的に媒介関数h(g)=xを導入して解く方が良いと考えます。
(別解)見通しの良い解き方
この解答で使った媒介関数h(g)には、h'(0)が存在しないので、h(g)を媒介関数にした置換積分の公式では、g=0も含めた積分区間で置換積分することができません。
しかし、上の計算では、
を導いて、それで式を置き換えて計算しています。
これは、h(g)の逆関数を媒介関数にして、その媒介関数のxによる微分を行う、逆向きの置換積分の公式を使っているという事を意味します。
逆向きの置換積分の公式では、h(g)がg=0という積分区間の端でも、逆関数の微分が可能であり、h(g)がg=0で微分不可能な問題が回避できています。
(次に考える事)
この解では、x≧0の場合の置換積分をしました。
x<0の場合の置換積分を媒介するもう1つの媒介関数p(g)も導入して、x<0の場合も解きます。
(別解おわり)
こうする事で計算の見通しが良くなりました。
こうして、直接的に媒介関数h(g)=xを導入すると、考え易くなったのは、連結区間[a,b]での関数f(x)の積分を媒介する関数x=h(g)およびx=p(g)は、積分変数gに関する単調増加関数か単調減少関数であることが明示されているからです。
この解き方では、置換積分の区間[a,b]が、x≧0と、x<0の区間に明確に細分化されました。そして、関数f(x)の各区間[a,b]毎に、関数f(x)の積分を媒介する関数x=h(g)とx=p(g)を使い分けることで考え易くなりました。この別解のように解くことは、置換積分の計算の見通しが良い良い解き方だと考えます。
(事例4)
以下の様な置換積分を考えてみます。
ここで、置換積分の公式を使うにあたって、積分変数xを積分変数gに置き換える関数h(g)で使えるのは、この関数h(g)が微分可能である変数gの閉区間[ga,gb]です。
その閉区間に関して、h(g)の、1つながりに連続な関数のみが、使える関数です。
よって、g>0で定義された1つながりに連続な関数h(g)が使える。
また、それとは異なる関数の、u<0で定義された1つながりに連続な関数p(u)が使える。
それらは異なる関数であるので、一緒にまとめて計算してはいけない。
先ず、関数h(g)を使って置換積分する。
次に、関数p(u)を使って置換積分する。
(事例4おわり)
上の解答において、関数h(g)と関数p(u)を一緒にして、t≠0で定義された1つの関数w(t)にしてしまうと、それは、t=0で分断された関数であって、連結区間[ta,tb]で1つながりに連続していないので使えない。
(不定積分できる関数は1つながりに連続な関数)
すなわち、その場合は、置換積分の条件である:
「被積分関数f(x)の積分変数xでの積分を媒介するx=w(t)となる関数w(t)が、xの連結区間[a,b]に対応するtの連結区間[ta,tb]内の全ての実数値のtにおいてtで微分可能」
という条件を満足していないからです。
(重要な注意)
上の解答の計算において、媒介変数gによる置換積分と、媒介変数uによる置換積分が、積分区間の符号が違うだけで、同じ式で表わせます。そのため、その2つの式を一緒にして媒介変数tと、t≠0で定義された1つの媒介関数w(t)を使って置換積分したい誘惑があります。
しかし、その誘惑に引っかかって、通常の不定積分に必要な条件の、不定積分できる関数は1つながりに連続な関数に限る(拡張した不定積分の場合を除く)という条件を無視した解答をするのは誤りです。そういう解答をしない様に注意しましょう。
(広義積分の工夫:妥協策)
媒介変数gによる置換積分と、媒介変数uによる置換積分は一緒にしてはいけないが、各置換積分の結果の変数xで表した不定積分は、広義積分の操作によって、1つながりに連続する関数にまとめる事ができます。
そのため、t>0とt<0の2つの閉区間の2つの関数をまとめて表す関数w(t)を2つの媒介関数の並行した計算として処理し、その2つの媒介関数を使って得た、変数xである2つの不定積分の部分を、1つながりに連続させてつないだ不定積分を計算しても良い。
そのように考えて計算するならば、x=w(t)を使った置換積分の計算も許されると考えます。これは、妥協した意見ではありますが、、、
(妥協案による解答)
ここで、x→0の極限で、
x>0の区間での不定積分と、
x<0の区間での不定積分を
1つながりの関数に連結する広義積分を行い、
x=0の場合も含めた以下の式を得る。

(広義積分の解答を書く場合には、良く説明する必要があります。ただし、高校数学では広義積分を扱わない。)
(解答おわり)
(置換積分を媒介する関数の条件)
なお、ここで、問題になる疑問として、変数xでの積分を媒介するx=w(t)となる関数w(t)が微分可能で無い場合は、
必ず積分不可能になるか、
という疑念があります。
その疑問への答えは、
「広義積分においては、関数w(t)が微分可能で無い点が疎らにあっても積分可能で置換積分の公式が成り立つ」
という答えになります。
疑問に対する答えが、これなので、w(t)が微分可能で無い場合を必ず避けなければならないと言うのは、広義積分においては、積分できない根拠にはならないと言わざるを得ません。
w(t)が微分可能という条件は、広義積分では、それで無ければならない、という必要条件では無く、それならば積分可能性が保障されるという安全弁である十分条件なのです。
そのように積分可能性が保障されている十分条件を満足する積分の解を組み合わせて広義積分に利用すれば良いという、積分の条件だと考えます。
この積分の事例では、変数tで表した不定積分は、t=0で連続な1 つながりに連続な関数では無いので、t>0における不定積分と、t<0における不定積分は異なる連続関数です。
しかし、それを変数xで表した不定積分では、
x→0の極限で、
x>0の区間での不定積分と、
x<0の区間での不定積分を
1つながりの関数に連結する広義積分を行うことで、
x=0の場合も含めた1つながりに連結した1つの連続関数の不定積分が得られる。
(置換積分の条件をどう扱えば良いか)
広義積分まで考慮すると、積分できない事は確実には分からなく、あいまいです。そのため、置換積分は、どの様に行ったら良いか。
それは、確実に置換積分が可能であると保証されている条件が成り立つ積分区間[a,b]毎に置換積分して、その個々の置換積分の結果の不定積分の部分を1つなぎに連続させた不定積分を計算すれば良いのです。
もしかしたら置換積分できるかもしれないが、確実に保証されていない区間は、別途、確実に置換積分が可能な条件が満足される手段を用いて置換積分すれば良いのです。
特に、高校生が置換積分の解答を書く場合は、f(x)が連続で、x=g(t)とする関数g(t)が微分可能でg'(t)も1つながりに連続である連結区間毎に置換積分して解答すべきと考えます。
ただし、g'(t)が存在しない点では、t=s(x)というg(t)の逆関数を使う逆向きの置換積分の公式を使って、g'(t)が存在しない問題を回避して解答します。
(更には、g(t)が単調増加関数か単調減少関数である連結区間に限った方が良いとも考えます。)
【(別ページ)変換する変数を関数で導入しても良い】
【1つのtの値に対して複数の値を持つ不定積分】
sin(x)をcos(x)で積分したらどうなるでしょうか。
重要な注意:
この様に、
sin(x)は、cos(x)=tに対して値が2つある関数です。
そういう関数は、同じ値のtに対して、異なる値の関数を使い分けて積分することになります。
それでは、置換積分を利用してこの問題を解いてみます。
(解答おわり)
(注意)
t=cos(x)の値が、-1から1までの範囲しか無いので、
不定積分∫f(x)dt は、tの定義域が-1から1までに限定された関数です。
その不定積分∫f(x)dtを変数xで表した上の解の式のxの定義域は、tの値が-1から1までになる変数xの範囲です。
その変数x範囲は、マイナス無限大からプラス無限大まで使えます。
t=cos(x)の値が、-1から1までの範囲しか無いのに、
その範囲で積分される被積分関数をxで表した式が、
同じt=cos(x)を与えても、そのtに対応する変数xによる被積分関数sin(x)の値が2つありました。
その結果、-1から1の範囲で積分した不定積分をxで表した式が、同じtに対応しても、xの値が異なる毎に異なる不定積分の値を持つ、不定積分の関数が得られます。
すなわち、不定積分∫f(x)dx=∫f(g(t))g'(t)dtは、与えられた1つのtの値に対して、複数の値を持つ多価関数になっています。
これは、単純な、f(g(t))g'(t)のtによる不定積分の形とは異なった形の解です。
なぜなら、被積分関数f(x)=sinxをtによって積分する被積分関数に変換した関数f(g(t))g'(t)の値が1つのtの値に対して2つあるからです。そして、同じ値のtに対して、異なる値の被積分関数を使い分けて積分するからです。
【変数変換の不思議】
《微分不可能が微分可能に変わる例》
(注意1)関数の変数を変換すると微分不可能な点が微分可能な点に変わることがある。
下図のグラフの関数は、O点では傾きが無限大なのでxで微分不可能です。
(x=0を積分区間に含む関数f(x)の積分を置換積分する関数g(t)には、下図の関数は使えない事に注意)
しかし、変数xを以下のグラフの関係を持つ変数tに変換してみます。
この変数tで元の関数をあらわすと以下のグラフになります。
このグラフはO点で、tで微分可能です。
このように関数の変数を変換する、変数xでは微分不可能だった関数の点が、変数tでは微分可能になる、ということが起こり得ます。
という関係があります。
有限の微分係数が存在する(微分可能)という状態は、変数を変換すると変わることがあります。
それは、微分する変数に応じる「微分可能」という条件が、
いわば、
「式を0で割り算する計算をしてはいけない」
という計算の縛りと似た意味を持つことを意味しています。
(注意2)関数の変数を変換すると微分不可能な点が微分可能な点に変わることがあるもう1つの例を考える。
下図のグラフの関数は、O点では、左側微分係数と右側微分係数が異なるのでxで微分不可能です。
しかし、変数xを以下のグラフの関係を持つ変数tに変換してみます。
この変数tで元の関数をあらわすと以下のグラフになります。
このグラフはO点で、tで微分可能です。
このように関数の変数を変換すると、変数xでは微分不可能だった関数の点が、変数tでは微分可能になる、ということが起こり得ます。
(注意3)関数の変数を変換すると、接する2つグラフが接さない2つのグラフに変換される例を考える。
下の2つの関数のグラフは、O点で同じ微分係数=0を持ち、O点で接しています。
しかし、変数xを以下のグラフの関係を持つ変数tに変換してみます。
(この関数のグラフは、t=0の点での微分係数が無限大になってしまい、t=0では微分可能ではありません)
この変数tで元の2つの関数をあらわすと以下の2つのグラフになります。
元の2つのグラフの変数xを変数tに変換した2つのグラフは、O点で変数tで微分すると異なる微分係数を持ち、O点で接さず交差しています。
変数を変換すると、このように、互いに接する2つのグラフが、接触する点での微分係数が異なる2つのグラフに変わってしまうことがあることに気をつけましょう。
すなわち、「2つの接するグラフが接点において等しい微分係数を持つ」ことが、グラフの座標変換によって変わってしまい2つのグラフの接触点での微分係数が等しく無くなることが有り得ます。
その様なおかしな事が起こる場合は、変数のその値で微分可能では無い関数を使って変数を変換すると生じ得ます。おかしな事が起こらないようにする1つの十分条件として、変数変換に使う関数を、変数のその値で「微分可能」な関数を使えば、変数がその値の部分でのグラフにはおかしな事が起こりません。
「微分可能」は、このようにおかしな事が起こらないようにする十分条件なのです。これが、「微分可能」と「微分不可能」を区別する意味だと考えます。
(交差している2つのグラフが、変数変換すると互いに接する2つのグラフに変わる例)
上図のように、変数tの関数f(t)とg(t)との2つの関数値をY=f(t)、及びY=g(t)とする。
f(t)=t
g(t)=t/2
とする。 この場合に、上図のように、2つのグラフが、tY座標平面上では互いに交差しているだけで、接していない。
このグラフの変数tを以下のグラフの関数であらわす媒介変数xを考える。
変数tをこのグラフの関数であらわす媒介変数Xを使うと、
XY平面上で先の2つのグラフをあらわすと以下の図の様になる。
x≧0の場合に:
関数f(t)=x2
関数g(t)=x2/2
になる。
この様にXY座標平面上では、互いに接する2つのグラフに変換されてしまった。
すなわち、接さずに単に交差しているだけの2つのグラフが、互い接するグラフに変わってしまった。
(無難な変数変換の条件)
tY座標平面上の2つのグラフがある変数値において接するか否かを調べている時に、そのように関数の性質が変わってしまわない、変数tと媒介変数xの変数変換の条件は、その2つのグラフが交差する点の位置の変数値において:
dt/dx ≠ 0
となることが必要です。
また、その関数が”微分可能”であることも必要で、すなわち、その2つのグラフが交差する点の位置の変数値において:
dt/dx ≠ ±∞
も必要です。
この2つの条件を満足する関数で変数変換をするならば、グラフの所定の点での「微分可能」または「微分不可能」というグラフの性質が変数変換の後でも同じに維持されます。
例えば、log(X)という関数は、X=0以外の点では、この2つの条件を満足します。
そのため、この関数を使って変数変換するならば、X=0以外の点では、「微分可能」と「微分不可能」という性質が変わりません。
(関数の性質を変えない変数変換の使用例)
以下の式1であらわされるグラフを考えます。
Y=xa (式1) (定数 a は所定の実数)
この式1であらわされるグラフは、
グラフが滑らかである大部分の変数値xにおいて、
傾きが∞にならない点で、微分可能です。
この式1のグラフの微分可能性は、以下の様に変数変換して調べることもできます。
この式1を関数log(x)で変換すると、
log(Y)=a*log(X) (式2)
に変換されます。
この式2を
Z=log(Y) (Z>0)
t=log(X) (t>0)
で変数変換すると、
Z=a*t (式3) (ただし、Z>0,t>0)
が得られます。
この式3であらわされるグラフは、元の変数であらわされたグラフと、「微分可能」と「微分不可能」という性質が変わりません。
式3のグラフは「微分可能」ですので、元の式1であらわされたグラフも「微分可能」であることがわかります。
なお、置換積分法での解き方が違うと積分の解の式の形が違うことがあります。それは、同じ解の式が異なる形で表れているだけですので、異なる形であっても、その解を受け入れるべきです。
「(別ページ)形が違う同じ式」
【置換積分の条件はどこまで緩められるか】
置換積分の条件になっている、
「関数g(t)が微分可能であること」
という条件は、
「導関数g'(t)が積分可能であること」
という意味で設定された条件でした。
しかし、
g(t)がある1点で微分可能でなくても、
g(t)が1つながりに連続な関数であれば 、
その微分が出来ない1点は無視して、それ以外の関数値
f(g(t))g'(t)
を使って、
tで積分するならば、
不定積分の置換積分の公式:

が成り立つ。
なぜなら、リーマン積分によって関数を微小区間に分割して微小な面積の総和を取る積分の定義を、以下の図の様に変えた積分を定義できるからである。
上の図では、リーマン積分での微小区間の領域を、極限では同じ領域になる少し狭めた領域に変え、その領域の面積の極限を狭める前の微小区間の面積と同じにする。
その微小面積の総和を積分とする広義積分を使う。
こういうふうに微小領域を設定すれば、積分区間の端での関数値が何であるかを無視して積分することができる。
積分区間の端で関数が無限大に発散するような現象も、狭められた領域における、区間の端の近傍の関数値が無限大に発散する事で反映されるので、見逃される事が無い。
広義積分によれば、積分区間の端で媒介関数の微分g'(t)が存在しない場合でも積分ができる。
(広義積分の解答を書く場合には、良く説明する必要があります。ただし、高校数学では広義積分は扱わない。)
また、例えば、
x=g(t)=t, (t≦0)
x=g(t)=2t, (t≧0)
という、t=0では微分できない関数g(t)を使った場合。
g'(t)=1, (t<0)
g'(t)=2, (t>0)
であって、g'(t)は、t=0で連続ではありません。
しかし、g(t)は、t=0 で連続です。
また、t=0の点で(導関数g'(t)が定義されていない)そのtの値の近傍までg'(t)を積分して、その積分の極限値をt=0の点等での値g(0)と定義する広義積分をするならば、
そういう積分を定義して使うならば、
t=0では連続で無い導関数g'(t)を持つ媒介関数g(t)を使っても、
上の式であらわした不定積分の置換積分の公式の右辺の積分が、
t=0の点をまたいだ積分が可能になります。
広義積分によって積分可能になる条件として、以下の条件が考えられる。
「閉区間で積分可能で、かつ、最大値と最大値を持つ(有界であると言う)」関数同士の積の関数も積分可能な関数になります。 そのため、
「関数g(t)が、まばらにある微分不可能な点以外では、微分可能な関数であって、微分不可能な点でも連続で1つながりに連続な関数である」ならば、置換積分の公式が成り立ちます。
また、f(x)も「閉区間で積分可能で、かつ、最大値と最大値を持つ(有界であると言う)」条件が成り立つならば、f(x)が連続でなくても、置換積分の公式が成り立ちます。
結局、置換積分可能の条件を緩める限り緩めれば、以下の条件になる。
「閉区間[a,b]において、積分可能な関数f(x)に関して、
変数x=g(t)とおくとき、
g(t)は、まばらには存在し得る微分不可能な点を除外した点で微分可能であり、微分不可能な点でも連続な1つながりに連続な関数である事。
そして、
関数f(g(t))は、
「閉区間[a,b]で積分可能で、かつ、最大値と最大値を持つ(有界であると言う)」関数である事」
が、広義積分において置換積分の公式が成り立つための、(必要十分条件にかなり近い)十分条件です。
(これが必要条件では無い例の1つは、「変換された被積分関数の性質が変わる」にある積分です。その例でも、広義積分において、置換積分の公式が成り立つからです。)
この条件は、関数のイメージが湧き易い以下の条件に変えると覚え易いかもしれない。
「関数g(t)は、疎らには存在し得る微分不可能な点を除外した点で微分可能である、微分不可能な点でも連続な1つながりに連続な関数であり、
関数f(g(t))は、区間内で数点を除いて連続であり、
その数点でも無限大には発散しない(最大値と最小値を持つ有界な)関数であること」
リンク:
高校数学の目次
(6)積分の知識:
「置換積分法」
(ページ内リンク)
▽置換積分の公式の定義
▽公式の第1の証明
▽公式の第2の証明
▽逆向きの置換積分の公式
▽(別ページ)被積分関数を0で割り算して良いのか?
▽(別ページ)広義積分
▽媒介する関数g(t)の条件
〇x=g(t)の関数は単調で無くても良い
〇関数t(x)=t が単調な関数では無い置換積分
〇単調で無い関数 g(x)=g で置換積分する例
□定積分を節約
▽望ましい置換積分方法(積分区間を分割する)
▽定積分する積分区間を間違えないコツ
▽(別ページ)広義積分を前提にしたtan(x/2)等の置換積分の計算事例
▽自由に変数変換できる置換積分の事例
〇見通しの良い解き方
▽(別ページ)変換する変数を関数で導入しても良い
▽1つのtの値に対して複数の値を持つ不定積分
▽変数変換の不思議
▽(別ページ)形が違う同じ式
▽置換積分の条件はどこまで緩められるか
高校生用の微分積分の教科書や参考書は不正確で、勉強用に不適切だと思います。高校2年生が微分積分を勉強するのに適切な参考書は、大学1年生向けの参考書:「やさしく学べる微分積分」(石村園子) ¥2000円 が良いと思います。
【置換積分法】
不定積分∫f(x)dx を求めるときに,積分変数を変換して積分する事を置換積分法といいます。
置換積分では、変数の変換に伴い、被積分関数が変更されます。その被積分関数の式の変形計算では、広義積分を用いる必要を生じるなどの、被積分関数の変形のルールを正しく把握する必要があります。また、変数の変換にともない、積分範囲が変更されます。そのため、積分の範囲のルールを正しく把握する必要があります。
そのように、置換積分にともなって、積分のルールが正しく把握されているかが問われます。以下では、そのルールの正確な情報を説明します。
しかしながら、ルールをあまり知らないでも、とにかく置換積分法に慣れて使い始めたい方もいると思います。その方には、ここをクリックした先で分かり易く説明しているサイト等を参考にしてください。そして置換積分法に慣れて心に余裕が出てきたら、このサイトに戻ってきて欲しいと思います。
例えば、以下のパターンの置換積分の第2の定理の適用に慣れてください。

《1つの例》

《もう1つの例》

《更にもう1つの例》

置換積分法は、以下の図の様に、
「積分する微小面積を、変数xでのグラフと変数tのグラフとで同じにして、積分した総面積を同じにする」
ように被積分関数f(x)を被積分関数h(t)に変換するものです。

(置換積分法の第1の定理)
関数f(x)が、変数xのある連結した区間内の全ての実数で定義された、1つながりに連続な関数である場合、
変数xを、微分可能な関数g(t)で、x=g(t)という式で変数tに変換すると、

が成り立つ。
(置換積分の第1の定理おわり)
(置換積分法の第2の定理=逆向きの定理)
置換積分法には、以下の、逆向きの置換積分の定理があります。
「生き抜くための高校数学」(芳沢光雄) の417ページに逆向きの置換積分の使い方の説明があります。
xで微分可能な関数s(x)でs=s(x)とした変数sを使った置換積分によって、以下のように変数xを変数sに変換して積分できます。

この、置換積分の第2の定理では、dx部分をdsに置き換えるのと同時に、f(x)部分をp(x)に置き換える際にf(x)をs'(x)で割り算してp(x)にしている。
あるx=aの点でs'(a)=0となる場合、そのx=aの点で、式を0で割り算する計算をしているので、これは、式の同値変形では無い。
しかし、被積分関数の分母にs'(a)=0という関数があっても、広義積分によって、積分した結果の関数が、x=aで極限値を持てば、その極限値をx=aでの積分の値であると定義できる。
そのため、s'(a)=0となる関数が分母に来て、積分の定義域からx=aとなる点が除外されても、広義積分によって、x=aでの関数の極限値が存在すれば、x=aの点を定義域に復活できる。また、その極限値が存在しないならば、x=aとなる点で関数が定義され無いことがそのままで正しいのです。そのため、s'(a)=0となる関数s'(x)が分母に来ても良いのです。
(置換積分の第2の定理おわり)
この置換積分の定理(置換積分の公式)は、以下の図の様に、
「積分する微小面積を、変数xでのグラフと変数tのグラフとで同じにすれば、積分した総面積も同じになる」
事を表した定理です。

(必要条件)ΔxもΔtも f(x)Δx=h(t)Δt も微小量であること。
また、微小面積が0になる場合までは考えていない。
それは当たり前で、無条件に成り立つ事のように思えるので、それが成り立つための条件を付ける事自体が余分でおかしな事の様に思えます。
しかし、無条件に成り立つわけではなく、
ΔxもΔtもf(x)Δx=h(t)Δt も微小量であることという必要条件が必ず成り立たなければなりません。
また、微小面積が0になる場合は、対象外です。
公式に付けた条件の、x=g(t)が微分可能であるという条件は、ΔxもΔtも微小量であるために必要な条件を数学的に記述したものです。
また、g(t)が微分可能であるという条件が満足できない場合には、変数xの区間を、公式の条件が完全に満たされる狭められた区間に分割し、その分割した区間毎に置換積分を行なう。それで得た複数の区間毎の不定積分を、分割した区間の端でつないで1つながりに連結した不定積分に拡張する。そうすれば、g(t)が微分可能で無い点で区間を分割して不定積分し、後で各区間の不定積分をつなげば良いので、公式の条件が満足できない場合にも対応できます。
【第1の定理の第1の証明】
(1)先ず、xを媒介変数 t であらわす関数g(t)は、tが変化したときにどのくらい変化するか調べる。
そのため、x=g(t)をtで微分する。

x=g(t)がtで微分可能、すなわち、(Δx/Δt)が有限の値ならば、
Δxが以下の式であらわされる。
(2)その場合に、以下の式が成り立つ。
以上の計算で、g'(t)の値が確定した有限の値でありさえすれば、たとえ、g'(t)が不連続な関数になってもかまわない。
(証明おわり)
【第1の定理の第2の証明】
置換積分法は、合成関数の微分の公式の同類です。
(証明開始)
先ず、
とすると,
である。
そこで
とおき,
を考えると,g(t)が微分可能であれば、
合成関数の微分の公式によって、
となる。
(合成関数の微分の公式はここをクリックした先を参照)
そして、その様にその関数 f(g(t))g'(t) の値が有限の範囲内にあれば、以下の式の左辺の積分が可能である。
(もしg'(t)が連続関数であれば、関数 f(g(t))g'(t) は連続関数になるので微分積分学の基本定理の条件が満足され、以下の式の左辺の積分が確実に可能である)

となります。
(証明おわり)
【第2の定理=逆向きの置換積分の定理】
置換積分の公式の概念は:

(必要条件)ΔxもΔtも f(x)Δx=h(t)Δt も微小量であること。
また、微小面積が0になる場合までは考えていない。
という概念に基づく公式でした。
微小面積が0になる場合を全く考慮せずに、
という条件に限定すると、
dx/dt≠0,
dt/dx≠0,
となってしまうので、
公式の制約が大きいです。
(場合1)dx/dt=0の場合
しかし、先に証明できた置換積分の第1の定理は、
dx/dt=0
の場合に適用できます。

とすると:
dx/dt=0
の場合にも使える第1の定理:
すなわち、
の場合に:
となる場合に、

を積分範囲に含んで、

が成り立つという置換積分の第1の定理が使えます。
(場合2)dt/dx=0の場合
dt/dx=0
の場合には、
x=g(t)の逆関数の

を使う第2の定理を使います。

すなわち、
の場合に、
となる場合に、
を積分範囲に含んで、

が成り立つので、この式を逆さにした、

という形の式の第2の定理=逆向きの置換積分の定理を使います。
しかし、このように式を逆向きにして使って良いとする論理には欠陥があります。
置換積分の第1の定理ならば、式h(t)が定義されていて、かつ、s'(x)が定義されているならば、変数tで積分する被積分関数h(t)を、変数xで積分する被積分関数f(x)に変換できます。この場合は、h(t)が定義されていれば、必ずf(x)が定義されます。しかし、第2の定理では、式f(x)が定義されているならば、必ず式h(t)が定義されるという保証は有りません。そのため、そのまま、第1の定理の式を逆にして、h(t)=f(x)/s'(x)=p(x)=h(t)を被積分関数にした積分を正当化する事には論理の欠陥があります。しかしながら、広義積分を適用することで、s'(x)=0の場合を無視して良くし、また、h(t)が定義されなくても積分を可能にしているのです。
(補足)---------
第2の定理の式は、置換積分する中間の式に、
dtとなる、dt=s'(x)dx
が出て来る式です。
置換積分の第1の定理では、
置換積分する中間の式に、
dxとなる、dx=g'(t)dt
が出て来ていました。
置換積分の第1の定理と第2の定理(=逆向きの置換積分)は、
xの関数s'(x)とdxをまとめたs'(x)dxを、ds(x)=dtに置き換えて考える(第2の定理)か、
dx=dg(t)を、tの関数g'(t)を使ったg'(t)dtに置き換える(第1の定理)か、だけの違いです。
s'(x)=1/g'(t)
であり、((dt/dx)=1/(dx/dt)とも表現できます)
g'(t)=1/s'(x)
です。((dx/dt)=1/(dt/dx)とも表現できます)
dx/dt=g'(t)が無限大になった場合に第1の定理は使えないのですが、s'(x)=0は存在するので、s'(x)を使った第2の定理を使って計算をする事が多いですが、それはごまかしです。第2の定理でも、「被積分関数を割り算する関数s'(x)が0でない」という、第1の定理での、g'(x)が存在するべき制約条件に対応する制約条件が必要だからです。しかし、広義積分を適用することで、被積分関数を割り算する関数s'(x)が0になっても問題無く積分できるようにしています。
(補足おわり)------------
例えば、
以下の積分を考えます。
ここで、以下の様に変数xを関数g(t)を使って変数tに変換する事を考えます。
この場合に、関数x=g(t)のグラフは下図のようになります。
t=1のとき、
g'(t)が無限大になり、有限の微分係数g'(x)=dx/dtが存在しないので、第1の定理が使えません。
その場合には、関数x=g(t)の逆関数t=s(x)を考えて、その関数s(x)の微分s'(x)=dt/dxを考えて、
関数s(x)を使うのであれば、微分係数dt/dx=s'(x)の値が有限の値になるので第2の定理を使う事が多いです。cos(x)=dt/dx=s'(x)としてcos(x)を置き換える以下の計算が行われています。
このようにして、逆向きの置換積分により、g(t)の逆関数t=s(x)を使って変数xを変数tに置換積分する積分ができたように見えます。しかし、この逆向きの置換積分の計算には、厳密には、s'(x)≠0という制限条件が必要です。しかし、広義積分を適用することで、s'(x)≠0という制限条件を無視しても良いのです。
リンク(別ページ)被積分関数を0で割り算して良いのか?
リンク(別ページ)広義積分
【媒介する関数g(t)の条件】
《g(t)が微分可能という公式の条件の意味》
置換積分の公式の前提条件にある、g(t)が微分可能であるという条件の意味は、第1の証明で使ったΔxを以下の式であらわすため。
そのために導関数g'(t)が存在する事が必要でした。
導関数g'(t)が存在しない点がある場合は、媒介関数g(t)の逆関数s(x)を考えて、
という変換を考える逆向きの置換積分の公式(第2の公式)を使って、
s'(x)dx=dt
という置き換えをしてxによる積分の式をtによる積分の式に変換してg'(t)が存在しない問題を回避します。それにより問題が回避できる根拠は広義積分によります。
積分区間の点で、導関数g'(t)が存在しない場合に、その点を除いて分割した積分区間で積分が可能です。そして、広義積分を用いて、g'(t)が存在しない点での積分の値を定め、その点で、分割した積分区間をつなぐことで、g'(t)が存在しなかった点を含む領域にわたる置換積分が可能です。
分割した積分区間の端点でg(t)は微分可能で無くてg'(ta)やg'(tb)が存在し無くても分割した積分区間の中でg(t)が微分可能であれば積分が可能です。
(広義積分の解答を書く場合には、良く説明する必要があります。ただし、高校数学では広義積分は扱わない。)
《変数gの定義式x=h(g)の関数の一部を切り出して使う事例》
以下の様に、変数xでの関数f(x)の積分を、変数xの定義域のうち、x≧0の部分を変数gのg≧0の定義域に対応させて、変数xを変数gに置き換えて置換積分する場合を考えます。
定義域がg≧0である変数gを媒介変数にして置換積分する場合は、先ずは、x≧0の区間内でのみ関数f(x)が置換積分できる。
(事例おわり)
この置換積分では、x≧0の区間内でのみ定義された不定積分の解が得られた。
(置換積分の条件が合っているか)
置換積分の条件は、
(1)ある連結区間[a,b]でf(x)が連続な関数である。
(2)その区間[a,b]内の全てのxの値をx=g(t)と表し、
g(ta)=a,g(tb)=bとなる関数g(t)が、
連結区間[ta,tb]又は連結区間[tb,ta]で微分可能である。
(3)その連結区間[ta,tb]又は連結区間[tb,ta]で、関数g(t)の値が、連結区間[a,b]から、はみ出さないものとする。
この事例では、x≧0の区間という狭められた区間[a,b]で、上記の置換積分の条件が成り立っている。上記の置換積分の条件の意味する事は、そういう条件を満足する区間に、関数f(x)及びh(g)の定義域を狭めて置換積分を行うという事を意味する。
(事例の続き)
この事例の置換積分では、関数f(x)のx<0の区間での不定積分はできていない。x<0の区間の不定積分は、以下の様に行なうことができる。すなわち、定義域がu<0である変数uをx<0の変数xに対応させる置換積分をすることができる。
そして、定義域がu<0である変数uを媒介変数にして、x<0の区間内で関数f(x)が置換積分できる。
(事例の続きのおわり)
この置換積分では、x<0の区間内で不定積分の解が得られた。
以上の媒介変数uによる式と媒介変数gによる式を合わせると、変数xの全領域での不定積分の式が得られた。
置換積分の関数の条件は、関数を積分する変数の連結区間[a,b]内での条件であり、その条件は連結区間を狭くすれば満足できるようになると認識するべき。
また、置換積分を考え易くするために、更に以下の関数の条件を加えても良い。
すなわち、連結区間[a,b]での関数f(x)の積分を媒介する関数x=h(g)は、単調増加関数か単調減少関数であるものとする。この条件の関数h(g)を用いて置換積分することが望ましいと考える。
そういう関数h(g)=xを用いる条件は、置換積分の区間[a,b]を細分化するだけで実現できる。その各区間[a,b]毎に、関数f(x)の積分を媒介する関数h(g)=xを定義して使えば良い。そうすれば、その関数h(g)の逆関数が存在する。それにより置換積分が行ない易くなるので、それが望ましい。
単調な関数を使って変数 x を変数 g に変換するという事は、変数 x と変数 g を1対1対応させることを意味する。そのように、変数同士を1対1対応させている条件の下では、等式の左右の項を各々2乗した等式を作る式変形は同値変形である。出来上がった等式は元の等式と等価な式である。そのように、多くの式変形が同値変形になるという便利さがある。
《x=g(t)の関数は単調で無くても良い》
第1(及び第2)の証明において、例えば、下の図の様に、g(t)が、a=g(ta)となるt=taから始めて、tとともに増加するが、g(tb)=bに達する前に、一旦減少して、再び増加して、g(tb)=bに達する関数であっても、この証明が成り立っている事に注意する事。
そういう関数g(t)を使って置換積分しても良いのです。

また、置換積分するf(x)の積分変数xの定義域を、ある連結区間[a,b]に狭くできれば、用いる関数g(t)は、その区間内のxを表す事ができるだけでも良い。その関数g(t)が、その連結区間の外のxの値を表す事ができなくても良いのです。
《関数t=t(x)が単調な関数では無い置換積分の例》
変数xでの関数f(x)の積分を、以下の様な、単調では無い関数t(x)であらわされる変数t=t(x)で置換積分することもできる。

この場合には、この関数t(x)を、図の点Mで2つの関数に分割して、それぞれの関数毎に置換積分する。
以下の積分を、以下のパターンの第2の置換積分の公式を使って置換積分する。

以下の積分を計算する:
先ずは、x≧0を定義域とする関数t(x)で置換積分する。

次に、x≦0を定義域とする関数t(x)で置換積分する。

この2つの置換積分を合成した置換積分にする。その際に式(3)と式(5)を省略して計算ができる。そして、その、省略できる式(3)と式(5)以外の式は同じ式なので、式(3)と式(5)以外の式だけを使って、2つの置換積分を1つにまとめた計算式で置換積分しても良い。
(事例おわり)
《関数g=g(x)が単調な関数では無い置換積分の例》
以下の様に、変数xでの関数f(x)の積分を、媒介変数g=g(x)を使って、第2の置換積分の公式で置換積分する事例を考える。
見通しの良い解答のためには、変数xの定義域を分割した区間毎に単調な変数変換の関数を用いて積分することが望ましい。そのため、以下の様に、変数xの区間毎に、変数変換の単調な関数h(g)=xとp(g)=xを定義して解く。

先ず、一旦は、以上の式2と式3で、変数xの定義域を分割した区間毎に、積分を媒介する単調な関数h(g)とp(g)を定義する。それらの関数は、逆関数が存在するので、積分の見通しが良くなるので嬉しい。
次に、式1を微分して式4を導き、以下の様に計算する。
(解答おわり)
この解は、式2と式3が計算に代入されず無駄にあるように見えますが、式2と式3は、変数xと変数gの対応関係を明確にしたという意味を持つので、必要な式です。
(単調で無い関数 g で置換積分し定積分の計算を節約)
ちなみに、この不定積分を使って、
x=−1からx=1まで、xの関数の定積分を求めると、
1の2乗−(−1)の2乗=0
になります。
それに対応する、
(x=−1から0)g=1から0まで
(x=0から1)g=0から1まで
のgの関数の定積分は、
それぞれの区間でgの関数の定積分の和を求め、
総体の定積分の結果は0
になります。
この場合は、以下の様に、媒介変数gを用いた積分の被積分関数は、g=1から0までの積分区間でも、g=0から1までの積分区間でも、同じgの関数になる。そのため、その被積分関数を積分の起点のg=1から積分の終点のg=1までの積分としても良い。
(解答開始)
(解答おわり)
しかし、媒介変数gによる積分区間が1~1のように見えるのはみせかけにすぎず、この積分の正しい区間は、
1→0→1
です。
この区間内に積分が不可能な点(例えば無限大に発散する点)が含まれている場合は、この積分はできません。
その正しい積分区間
1→0→1
で、関数が異常になる点が無いかどうかを点検した上で、積分区間を
1→1
に節約して積分ができるのです。
(定積分の計算の節約の説明おわり)
(補足)
この問題の置換積分を逆にして、変数gによる積分を、第1の置換積分の公式を使ってg=g(x)として、変数xによる積分に変換する置換積分を考える。すなわち、以下の計算を考えます。
第1の置換積分の公式の証明では、関数g=g(x)が単調増加な関数で無くても公式が成り立っています。そのため、以上の計算には全く問題がありません。このように、単調では無い関数g=g(x)を使って置換積分しても良いのです。
(補足おわり)
このように、置換積分の公式は、第1の置換積分の公式と合わせて、第2の置換積分の公式も使え、双方向の変数変換の置換積分の公式が使えます。単調な関数h(g)の逆関数s(x)を使って、式を逆向きに置換積分する第2の置換積分を考えると、積分の過程が明確になって理解し易くなります。媒介関数h(g)の微分可能性が妨げになっても、その逆関数の媒介関数s(x)の微分可能性は妨げにならなければ、妨げが少ない関数を使って第2の置換積分をします。(しかし、その妨げが避けられている本当の理由は、広義積分をしているからです)
《導関数g'(t)は連続で無くても良い》

参考書によっては、導関数g'(t)も連続な関数である(「連続微分可能」とも言う)場合を、置換積分の公式が成り立つ条件としている参考書もあります。しかし、その条件が無くても公式は成り立ちます。以下で、その理由を説明します。
「関数g(t) を微分した導関数g'(t)も連続な関数である」
という条件が加えられる理由は、
導関数g'(t)が連続な関数であれば、それと何か連続な関数との積も連続関数になり、連続な関数は積分可能だから、置換積分の公式を証明し易くするために設定された条件でした。
しかし、連続な関数で無くても積分可能な関数はあります。g(x)のある点で微分が出来なくても、その点でg'(x)が発散しない限り、g'(x)は、その点も含んだ積分区間で積分が可能です。
また、第1の証明の中での前提条件は、g'(x)が有限の値である事であって、g'(x)が連続である事は証明には必要ありませんでした。
そのため、この条件は、本来は必要ない。(この条件は、置換積分を把握し易く考え易いようにするために加えられた条件です。この条件を守って置換積分するならば、計算の見通しが良くなり計算ミスを防ぐ事ができます。)
「本来は、g(x)が微分可能で、g'(x)が存在する」という条件だけで充分と考えます。
「微分可能関数の導関数は、中間値の定理も満たすので連続関数に極めて近い関数ではないか」
(微分可能な関数g(x)の導関数g'(x)が不連続な例)
g(x)を以下で定義する原始関数F(x)とし、
g'(x)=f(x)とすると、
f(x)=g'(x)は、
F(x)=g(x)の微分で作られたので、積分可能です。
(F(x)=g(x)の定義)
x≠0の場合:
x=0の場合: F(0)=0,
(導関数f(x)=g'(x))
原始関数F(x)=g(x)はx≠0の場合も、x=0の場合も、微分可能で、
その導関数f(x)=g'(x)は、以下の式であらわせます。
x≠0の場合の微分:
になり、xが0に近づくと-1と1の間を振動します。
この導関数が含むcos(1/x)の関数が以下のグラフであらわす形の関数になるからです。
X=0の場合にも、F(x)は微分可能で:
というように、0になります。
このように、x=0の場合の導関数f(x)=g'(x)は、x=0で不連続ではありますが、f(0)=0という値を持ちます。
この導関数f(x)=g'(x)は、x=0で不連続ですが、x=0で関数値を持ち、積分すると原始関数F(x)=g(x)になる、積分可能な関数です。
しかも、その積分結果の原始関数F(x)=g(x)を微分すると、元の、x=0で不連続な関数f(x)=g'(x)が得られます。
この様な関数g(x)を使って置換積分をした場合、関数g'(x)は細かく振動しますが、関数値が無限大に発散する事が無く有限な値を持つ積分可能な関数です。
g'(x)は積分可能なので、それを含む置換積分の公式も成り立ちます。
そのため、
そういう事からも、置換積分の公式の条件は、「g(x)が微分可能で、g'(x)が存在する」という条件だけで充分のように考えます。
《関数g(t)は完全に微分可能で無くても良い》
「関数g(t)が微分可能な関数である」条件は、広義積分においては、変数tの定義域内の疎らな点で関数g(t)が微分可能で無くても、それ以外の区間でg(t)が微分可能であれば置換積分が成り立ちます。
合成関数の微分の公式が成り立つので、置換積分の公式が成り立ちました。
しかし、合成関数の微分の公式が成り立たない場合にも置換積分の公式が成り立つ事がある事に注意する必要があると考えます。
ある1点tにおいて、
例えば、g(t)が微分可能では無くて、合成関数の微分の公式:
が成り立たない点があった場合。
その点を除外した、その点の両側の連結区間で、各々積分ができます。
そして、その積分の後で、その1点tの両側の積分区間での積分結果の関数を1つながりに連結する事もできる。そういう操作(広義積分)で得た関数では、

が成り立ちます。
すなわち、被積分関数の積分変数xの連結区間[a,b]の中に、合成関数の微分の公式が成り立たない1点が含まれていても、広義積分の不定積分では、置換積分の公式が成り立つ事があります。
この点で、広義積分における、置換積分の公式は、合成関数の微分の公式とは異なります。
g(x)が微分可能ということは、広義積分においては、積分区間の全域で完全に成り立っていなくても良いのです。
【不定積分の区間は開区間(a,b)にもできる】
不定積分の置換積分の公式は、積分範囲を、区間の端を含めない開区間(a,b)にしても成り立つ。
定理3.4 (置換積分法)
ある連結開区間(a,b)でf(x)が連続な関数である場合
(その場合は、その開区間の端ではf(x)及びその不定積分が無限大に発散する事があり得るが、(a,b)に含まれる閉区間での定積分は無限大にはならない)、
変数x=g(t)とおくと、g(t)が微分可能であれば、

が成り立つ.
(公式の定義おわり)
この様に、不定積分の区間を連結する開区間(a,b)にする場合は、g(t)の微分可能性の条件も、区間の端を考えないで良いので単純に開区間(ta,tb)又は(tb,ta)で微分可能であるだけで良くなり、分かり易くなる。
ここで、開区間(a,b)で関数f(x)の不定積分を求めた場合、その不定積分が定義される開区間(a,b)をはみ出した区間で定積分してはいけません。例えば、区間の端点を含めた閉区間[a,b]で定積分してはいけません。
また、媒介関数g(t)が微分可能で無く置換積分の条件が成り立たない場合に先ず行う事は、
逆向きの置換積分を行うと良いと考えます。
すなわち、媒介関数g(t)の逆関数s(x)を考えて、
という変換を使う逆向きの置換積分の公式を使って、以下の式の形の公式を使って積分変数を変換すれば良いのです。
この式で、
s'(x)dx=dt
という置き換えによって、
dxをdtに変換すれば良いのです。
このようにして、媒介関数g(t)=x がtで微分可能でなかった問題を回避します。(ただし、先に説明したように、s(x)を使う逆向きの置換積分の計算によっても、g(t)が微分可能で無かった問題は解消していません。広義積分の概念によってこの問題が解消するのです。)
(定積分の置換積分の公式について)
また、定積分の積分区間は、必ず端がある閉区間[c,d]です。そのため、定積分の置換積分の公式は、積分区間が閉区間に限定された場合の公式になります。その点で、定積分の置換積分の公式は、不定積分の置換積分の公式と違ってきます。
【望ましい置換積分方法】《積分区間を分割する》
置換積分の変数xを変数tに変換する関数g(t)=x に単調な関数を用いるという条件が大切です。その条件を緩めても置換積分が可能な場合がありますが、関数g(x)に単調で無い関数を用いる事は望ましく無い。
なぜならば、単調な関数には逆関数が存在するので、積分の計算の見通しが良くなる利点があるからです。
(積分区間を分割して、それぞれで積分する)
媒介関数g(t)=xを単調な関数にするには、変数xの定義域を、関数g(t)が単調になる区間毎に分割する。その区間毎にg(t)が単調な関数になるので、各区間で、g(t)の逆関数が存在する。その区間毎に不定積分を求め、それらの不定積分を連結して1つながりに連続な不定積分を求める広義積分を行なえば良い。それにより、関数g(t)を単調で無い関数(逆関数が存在しない)にした場合と同じ積分ができる。そのため、変数xの定義域を、関数g(t)が単調な関数になる区間に分割して、見通しの良い計算をする事が望ましいのです。

(1)
考え易い関数を使って置換積分の条件を単純化するために、以下の関数を使うことが望ましい。
すなわち、積分を媒介する関数x=g(t)は、1つながりに連続であって、単調増加関数か単調減少関数であるものとする。
単調増加関数か単調減少関数には必ず逆関数が存在するので、逆関数の概念も使って積分の計算が進められ計算の自由度がとても大きくなる効果があります。
(2)
もし、媒介関数g(t)=xがある積分区間で単調な関数で無ければ、g(t)=xが単調である区間に積分区間を分割する。そうすれば、その分割された積分区間でg(t)=xが単調な関数になる。その各区間毎に置換積分すれば良いのです。
x=g(t)は、すなわち、媒介変数tによる関数g(t)の値は、変数xの全部の範囲をカバーしないで良いのです。被積分関数が変数xによって定められる変数xの全区間の一部の区間をカバーするだけで良いのです。
(3)
区間[a,b]に限って置換積分して不定積分を求める。その区間[a,b]に隣接する区間[c,d]で置換積分して不定積分を求める。それらの不定積分の関数同士が、閉区間が隣接する境界の極限で1つながりに連続に連結できるかを考える。
すなわち、不定積分の部分として、確実に置換積分可能に範囲を狭めた連結区間[a,b]や連結区間[c,d]での不定積分の部分を複数求め、その関数を連続につないで1つながりに連続した不定積分を作るという広義積分を行なえば良いのです。
(「積分可能の定義」のページで説明した、部分部分の関数の接続方法と同じです。)

その1つながりに連続した解の関数は、置換積分可能な媒介関数g(t)の制限を可能な限り緩めて置換積分して得た不定積分の解と同じです。
(4)
その様に、後で不定積分の部分を連結する事を前提にして、以下の様に、置換積分する関数の条件が満足される(分割された)連結区間[a,b]を求める。
(A)関数f(x)の、ある連結区間[a,b]で連続な部分を考え、
(B)また、その連結区間[a,b]内の全てのxの値をx=g(t)と表す、g(ta)=a,g(tb)=bとなる1つながりに連続な関数で、
tの区間の端を除いた連結区間(ta,tb)又は連結区間(tb,ta)の点でtで微分可能な関数g(t)を考える。
(C)また、関数g(t)の値が、変数tの連結区間[ta,tb]又は連結区間[tb,ta]で、単調増加か単調減少であるように、tの連結区間[ta,tb]又は連結区間[tb,ta]とxの連結区間[a,b]を定める。
(D)g(t) をtで微分した導関数g'(t)も連続な関数となる(連続微分可能)関数g(t)を使う。
(E)それらの条件が成り立つxの連結区間[a,b]とtの連結区間内で定義される不定積分:

を求める。
(5)
そうして、xの連結区間[a,b]毎に別々にf(x)の不定積分を計算する。そして、それらのf(x)の不定積分の各連結区間[a,b]の境界で不定積分が極限で連結されると、1つながりに連続な関数に連結できるかを考える。その1つながりに連続する関数を、広義積分における、置換積分された不定積分の関数とする。
このようにして、見通しの良い関数を使って置換積分する事が望ましいと考えます。
【定積分する積分区間を間違えないコツ】
後で説明する、置換積分を媒介する関数g(t)の条件を緩められる事の説明の中の事例のように、被積分関数が不連続であっても積分できることがある。
そのため、被積分関数が連続であるか否かという、積分可能の判定条件は、広義積分においては、便宜的な十分条件であって、積分可能のための必要条件ではありません。
広義積分における置換積分の公式の必要十分条件(積分可能の条件)は、積分可能の定義のページで説明した様に、
不連続な関数f(x)に対しても、
その定義域を、関数f(x)の連続で無い点を除外した連結区間に分割し、
それら各連結区間毎に不定積分を計算し、
得られた各不定積分を連続につないで1つながりに連続な不定積分を構成します。
その不定積分を使って
F(b)-F(a)
の式で定積分を計算して良いのです。
この、
「積分結果の不定積分の関数F(x)が積分区間[a,b]で1つながりに連続する」
という条件が、
拡張した置換積分の公式においても、公式が成立する区間[a,b]を定めるための必要十分条件であると考えます。
(もう1つの注意点)
不定積分する積分区間は、
f(x)を積分する積分変数xが積分区間内を動くとき、
被積分関数f(g(t))g'(t)を積分する積分変数tが、どの点からどの点まで動くかを調べる事が必要です。
その積分範囲は、
被積分関数f(g(t))g'(t)を変数tで不定積分して得た関数H(t)が連続で無い点をまたぐ範囲ではないハズです。
関数H(t)が連続で無い点をまたいだ範囲を積分範囲と考えてはいけません。
その積分の範囲が、例えば、
t=taからt=∞、
t=-∞から、t=tb
までというように、積分変数tの積分範囲が分断された区間になる場合もあります。
そのように区間が分断されている場合は、
H(∞)-H(ta)==Aと、
H(tb) -H(-∞)=B
とを分けて求めて、
A+Bを求めれば良いのです。
【関数の微分可能性が公式を制約する】
置換積分の公式は、合成関数の微分の公式を使って証明できます。そのため、合成関数の微分の公式の同類です。
また、それ以外の同様な式で表された式を含む以下の公式群の同類です。
この各公式には、先ず、以下の縛り(成立条件)があります。
その縛りというのは、
「上の式の様に微小量の割り算であらわした式の、ΔhもΔxもΔtも、何れも微小量でなけばならない」
とういう条件です。
(例題)
例えば、
被積分関数(dh/dx)=f(x)の変数xによる積分を、
媒介変数 t と、
媒介関数g(t) =(1/t)= x
を使って置換積分する場合、
Δx=Δg=Δ(1/t)が、
t→0で、微小量にならないから、
t→0の場合には、関数g(t) =(1/t)= x を媒介関数に使うことができません。
(媒介関数g(t)は、t=0で微分可能で無い)
そして、各関数の微分可能条件を(あたりまえの条件のように見えますが)意識する必要がある事に気をつけてください。
「関数が微分可能(有限の値の確定した値の微分係数が存在する)」
という意味は、
「関数が、その変数のその値に限って、その変数で微分可能であれば良く、その変数のその他の値での関数の微分可能性は関係しない」
という意味です。
広義積分では、後で説明するように、変数 x での積分を、媒介変数 t での積分に変換する置換積分の媒介関数g(t)=x の条件を緩められます。
それを考えると、
置換積分を媒介する関数g(t)=x が、t=0近くで、
「媒介関数g(t)=x が、微分不可能な点の t=0 以外の点では微分可能で、t=0 の点も含めて1つながりに連続である」ことが、
広義積分において、被積分関数h(g(t))g'(t)が媒介変数tで積分可能であるために本質的に必要な条件であると考えます。
例題で、媒介関数g(t) =(1/t)を置換積分に使った場合、t=0では、
「媒介関数g(t)が1つながりに連続である」条件が成り立ちません。
そのため、広義積分においても、
t→0の場合には、関数g(t) =(1/t)を使うことができません。
(積分できない変数xの範囲に気をつける)
下図の関数f(x)は、x=0の点では関数f(x)の値が-∞になり、関数が定義されていないで、関数が不連続です。そして、この関数では、x=0を含んだ範囲で積分することはできません。
上図の関数を、上図の様にx=0を含む区間で定積分したら、マイナスの無限大になるので、積分が不可能です。
そのため、上図の関数を、例えば-1から1までの区間で積分する事も不可能です。
そのため、この関数f(x)の不定積分の変数xの定義域の閉区間は、x=0を含む事ができません。
これを無視して、関数f(x)の不定積分F(x)の変数の定義域にx=0を入れてしまうと以下の間違いをおかします。
F(x)=1/xをxで微分したら
になります。
そして、変数xで積分する区間内に、f(x)が発散する点のx=0を含めた、xが-1から1までの区間で、
関数f(x)の定積分を、F(x)を使って、 F(1)-F(-1)=1-(-1)=2
という 計算で求めると、明らかに間違えます。
上の図で明らかな様に、-1から1までの範囲でのf(x)の積分はf(x)のグラフの面積にならなければなりません。そのため、定積分の答えは、マイナス無限大にならなければなりません。そのため、 F(1)-F(-1)=2は、明らかに間違っています。
こういう間違いを、置換積分の計算でもおかさないために、置換積分の計算において、常に、積分範囲が適切であるかに注意しなければなりません。
以下では、被積分関数f(x)の変数xでの不定積分を媒介変数 t での不定積分に置換積分する場合を考えます。
という計算をして不定積分を求める場合に、
積分可能な範囲が、
x<0,
または、
x>0
である事を認識します。
すなわち、式の変形の過程で出てくる
「微分(dx/dt)や(dt/dx)が微分可能となる積分変数xや積分変数tの連結区間の範囲のみで、積分が可能である」
と考えて、
この不定積分を用いて定積分できる積分可能な範囲がどこからどこまでになるかを、注意深く考えながら、
積分の式の変形をしてください。
例えば、1つながりに連続なf(x)の不定積分を、
1つながりに連続なh(t)を使って、以下の計算で求める。
(第1の積分)
その後に、未だ不定積分をしていない、以下の1つながりに連続なf(x)を、以下の1つながりに連続なh(t)を使って、以下の様に不定積分する。
(第2の積分)
以上の2つの不定積分を同時に行なってはいけません。
第1の積分により、第2の積分も終わっていると考えないようにして下さい。
1度に不定積分できる範囲は、関数f(x)が1つながりに連続な区間内のみだからです。
(悩ましい問題)
置換積分に限らず、1度に不定積分できる範囲は、関数f(x)が1つながりに連続な区間内のみです。
以下の、1つながりに連続な関数f(x)の不定積分を、
以下の様にして不定積分する。
(第1の積分)
その後に、未だ不定積分をしていない、以下の1つながりに連続なf(x)を、以下の様に不定積分する。
(第2の積分)
以上の2つの不定積分を、第1の積分により、第2の積分も終わっていると考えないようにしてきたでしょうか。
1度に不定積分できる関数f(x)は、1つの、1つながりに連続な関数だけです。
しかし、今までの不定積分では、x>0の区間で1つながりに連続な関数と、x<0の区間で1つながりに連続な関数を、区別して別々の不定積分としてこなかったと思います。
(その積分では不定積分のルールが守られていないので、悩ましい問題だと思います。)
しかし、置換積分で自由自在に変数変換をするようになると、少しのルール違反も計算を誤らせる事になります。
そのため、置換積分では、そのルール違反はもはや見逃せなくなっています。
なお、関数が不定積分できた積分変数xの積分区間の判定方法は:
不定積分ができた積分変数xの範囲は、
不定積分の関数が、1つながりに連続な連結区間です。
不定積分が1つながりに連結する積分変数xの区間を1単位にし、
その1単位毎の関数は、異なる不定積分の関数とします。
上の例:
(第1の積分)
(第2の積分)
では、
x<0, での t+C という不定積分と、
x>0, での t+C という不定積分とは、
異なる関数だと言えます。
(不定積分を表す関数の変数tの定義域が異なれば異なる関数だからです)
なお、関数 f(x)が定義される変数xの連結区間からはみ出させた値cの点を経由する変数xの積分区間
(始点aから経由点cを経由して終点bまで至る積分区間)
でf(x)を積分した値は、
終点bでの不定積分F(x)の値と始点aでの不定積分F(x)の値の差 F(b)-F(a) とは異なった値になります。
【自由に変数変換できる置換積分の事例】
(事例1)
以下の不定積分を置換積分で求めてみます。
x≧-1の場合に:
【解答】
積分変数xを以下の積分変数tに変換する。
(解答おわり)
この不定積分は、積分変数を、ここをクリックした先のサイトのように変換して解く事もできます。解を得るための積分変数の変換方法は、その様に、かなりの自由度があります。
(事例1おわり)
【いつ置換積分を考えるべきか】
置換積分とは、積分変数の変換です。積分変数の軽い変換、例えば、x→t+Aや、x→2t等の変換をしたらどうなるかは、常に思考実験する(解答には書かないが)心がけが必要です。
次に、それより重い積分変数の変換、例えば、sinx=t 等を試す。
積分変数の軽い変換は、いつだって(解答に書かないでも)思考実験で試して、良い変換を思いついたら、いつでも使えるようにするべきです。
積分変数の軽い変換(x→t+Aや、x→2t 等)を常に思考実験するのは、積分の式の変形の可能な未来を見通すという事であって、解を考える時にはいつでも必要な事です。
積分変数の重い変換も、その次に頻繁に発想し、その重い変換の結果で式がどう変わるかの、変数の変換の経験を憶えていくと良いと思います。
こういう式になったら、x→2t に変換する、というのでは無く、
思考実験でx→2t に変換したら式がきれいになった時に、x→2t に変換する置換積分の式を解答の式に書くのです。
(小手わざ)
以下の様に変換できるという小手わざを覚えておいて使うと計算が楽になると思います。
この小手わざは体で自然に覚えておいて、分母にsin(β)がある関数をβで積分するときに、体が思い出して、β=2θとして変数を t に変換して使うようにできると便利だと思います。
(事例2)
以下の各事例では、置換積分による積分変数の変換がどこまで自由に変換できるかを考えていきます。
考え易い関数を使って置換積分の条件を単純化し、積分を媒介する関数x=g(t)は、単調増加関数か単調減少関数であると限定して考えて良い。
そういう限定をして、単調増加(又は、単調減少な)関数 f(x)と、その逆関数g(y)を考えます。
この場合、以下の積分を以下の様に置換積分する事ができます。
この様に、yをxの関数とした積分を、xをyの関数とした積分に置き換える置換積分が可能です。
同様にして、以下の積分を以下の様に置換積分する事が可能です。
以上の様に、置換積分法では、変数xと変数yを対等であると考えて、変数を置き換えて置換積分します。
変数yが変数xの関数であるとして変数xで積分していた積分を、変数xが変数yの関数であるとして変数yで積分する積分に置き換えるというダイナミックな変数の切り替えを行うのが置換積分法の特徴です。
このような変数変換を利用すると、ここをクリックしたサイトの逆関数の積分も解けるようになります。
(事例2おわり)
(事例3)
以下の様に、変数xでの関数f(x)の積分を、媒介変数gで置換積分する場合を考えてみます。
(注意)
変数xの正と負の定義域を持つ関数g=g(x)は単調な関数では無いので、逆関数を持たない。しかし、変数xが正の定義域でg(x)であると定義された関数は単調な関数なので逆関数を持ちます。xが負の定義域でg(x)であると定義された関数も、同様です。
この被積分関数を積分変数gのみで表そうとすると、以下の2つの場合に分かれます。
第1の場合:
もう1つの場合:
この様に、置換積分の結果が、積分変数xの2つの区間で別れた、異なる積分変数gの式であらわされる、xの定義域が異なる2つの関数になった。
そのため、この解の不定積分を使って定積分する場合は、以下の様に計算します。
(事例3おわり)
この事例3は、解の見通しが良くなかったと思います。見通しの良い解にするには、以下の様に、直接的に媒介関数h(g)=xを導入して解く方が良いと考えます。
(別解)見通しの良い解き方
この解答で使った媒介関数h(g)には、h'(0)が存在しないので、h(g)を媒介関数にした置換積分の公式では、g=0も含めた積分区間で置換積分することができません。
しかし、上の計算では、
を導いて、それで式を置き換えて計算しています。
これは、h(g)の逆関数を媒介関数にして、その媒介関数のxによる微分を行う、逆向きの置換積分の公式を使っているという事を意味します。
逆向きの置換積分の公式では、h(g)がg=0という積分区間の端でも、逆関数の微分が可能であり、h(g)がg=0で微分不可能な問題が回避できています。
(次に考える事)
この解では、x≧0の場合の置換積分をしました。
x<0の場合の置換積分を媒介するもう1つの媒介関数p(g)も導入して、x<0の場合も解きます。
(別解おわり)
こうする事で計算の見通しが良くなりました。
こうして、直接的に媒介関数h(g)=xを導入すると、考え易くなったのは、連結区間[a,b]での関数f(x)の積分を媒介する関数x=h(g)およびx=p(g)は、積分変数gに関する単調増加関数か単調減少関数であることが明示されているからです。
この解き方では、置換積分の区間[a,b]が、x≧0と、x<0の区間に明確に細分化されました。そして、関数f(x)の各区間[a,b]毎に、関数f(x)の積分を媒介する関数x=h(g)とx=p(g)を使い分けることで考え易くなりました。この別解のように解くことは、置換積分の計算の見通しが良い良い解き方だと考えます。
(事例4)
以下の様な置換積分を考えてみます。
ここで、置換積分の公式を使うにあたって、積分変数xを積分変数gに置き換える関数h(g)で使えるのは、この関数h(g)が微分可能である変数gの閉区間[ga,gb]です。
その閉区間に関して、h(g)の、1つながりに連続な関数のみが、使える関数です。
よって、g>0で定義された1つながりに連続な関数h(g)が使える。
また、それとは異なる関数の、u<0で定義された1つながりに連続な関数p(u)が使える。
それらは異なる関数であるので、一緒にまとめて計算してはいけない。
先ず、関数h(g)を使って置換積分する。
次に、関数p(u)を使って置換積分する。
(事例4おわり)
上の解答において、関数h(g)と関数p(u)を一緒にして、t≠0で定義された1つの関数w(t)にしてしまうと、それは、t=0で分断された関数であって、連結区間[ta,tb]で1つながりに連続していないので使えない。
(不定積分できる関数は1つながりに連続な関数)
すなわち、その場合は、置換積分の条件である:
「被積分関数f(x)の積分変数xでの積分を媒介するx=w(t)となる関数w(t)が、xの連結区間[a,b]に対応するtの連結区間[ta,tb]内の全ての実数値のtにおいてtで微分可能」
という条件を満足していないからです。
(重要な注意)
上の解答の計算において、媒介変数gによる置換積分と、媒介変数uによる置換積分が、積分区間の符号が違うだけで、同じ式で表わせます。そのため、その2つの式を一緒にして媒介変数tと、t≠0で定義された1つの媒介関数w(t)を使って置換積分したい誘惑があります。
しかし、その誘惑に引っかかって、通常の不定積分に必要な条件の、不定積分できる関数は1つながりに連続な関数に限る(拡張した不定積分の場合を除く)という条件を無視した解答をするのは誤りです。そういう解答をしない様に注意しましょう。
(広義積分の工夫:妥協策)
媒介変数gによる置換積分と、媒介変数uによる置換積分は一緒にしてはいけないが、各置換積分の結果の変数xで表した不定積分は、広義積分の操作によって、1つながりに連続する関数にまとめる事ができます。
そのため、t>0とt<0の2つの閉区間の2つの関数をまとめて表す関数w(t)を2つの媒介関数の並行した計算として処理し、その2つの媒介関数を使って得た、変数xである2つの不定積分の部分を、1つながりに連続させてつないだ不定積分を計算しても良い。
そのように考えて計算するならば、x=w(t)を使った置換積分の計算も許されると考えます。これは、妥協した意見ではありますが、、、
(妥協案による解答)
ここで、x→0の極限で、
x>0の区間での不定積分と、
x<0の区間での不定積分を
1つながりの関数に連結する広義積分を行い、
x=0の場合も含めた以下の式を得る。

(広義積分の解答を書く場合には、良く説明する必要があります。ただし、高校数学では広義積分を扱わない。)
(解答おわり)
(置換積分を媒介する関数の条件)
なお、ここで、問題になる疑問として、変数xでの積分を媒介するx=w(t)となる関数w(t)が微分可能で無い場合は、
必ず積分不可能になるか、
という疑念があります。
その疑問への答えは、
「広義積分においては、関数w(t)が微分可能で無い点が疎らにあっても積分可能で置換積分の公式が成り立つ」
という答えになります。
疑問に対する答えが、これなので、w(t)が微分可能で無い場合を必ず避けなければならないと言うのは、広義積分においては、積分できない根拠にはならないと言わざるを得ません。
w(t)が微分可能という条件は、広義積分では、それで無ければならない、という必要条件では無く、それならば積分可能性が保障されるという安全弁である十分条件なのです。
そのように積分可能性が保障されている十分条件を満足する積分の解を組み合わせて広義積分に利用すれば良いという、積分の条件だと考えます。
この積分の事例では、変数tで表した不定積分は、t=0で連続な1 つながりに連続な関数では無いので、t>0における不定積分と、t<0における不定積分は異なる連続関数です。
しかし、それを変数xで表した不定積分では、
x→0の極限で、
x>0の区間での不定積分と、
x<0の区間での不定積分を
1つながりの関数に連結する広義積分を行うことで、
x=0の場合も含めた1つながりに連結した1つの連続関数の不定積分が得られる。
(置換積分の条件をどう扱えば良いか)
広義積分まで考慮すると、積分できない事は確実には分からなく、あいまいです。そのため、置換積分は、どの様に行ったら良いか。
それは、確実に置換積分が可能であると保証されている条件が成り立つ積分区間[a,b]毎に置換積分して、その個々の置換積分の結果の不定積分の部分を1つなぎに連続させた不定積分を計算すれば良いのです。
もしかしたら置換積分できるかもしれないが、確実に保証されていない区間は、別途、確実に置換積分が可能な条件が満足される手段を用いて置換積分すれば良いのです。
特に、高校生が置換積分の解答を書く場合は、f(x)が連続で、x=g(t)とする関数g(t)が微分可能でg'(t)も1つながりに連続である連結区間毎に置換積分して解答すべきと考えます。
ただし、g'(t)が存在しない点では、t=s(x)というg(t)の逆関数を使う逆向きの置換積分の公式を使って、g'(t)が存在しない問題を回避して解答します。
(更には、g(t)が単調増加関数か単調減少関数である連結区間に限った方が良いとも考えます。)
【(別ページ)変換する変数を関数で導入しても良い】
【1つのtの値に対して複数の値を持つ不定積分】
sin(x)をcos(x)で積分したらどうなるでしょうか。
重要な注意:
この様に、
sin(x)は、cos(x)=tに対して値が2つある関数です。
そういう関数は、同じ値のtに対して、異なる値の関数を使い分けて積分することになります。
それでは、置換積分を利用してこの問題を解いてみます。
(解答おわり)
(注意)
t=cos(x)の値が、-1から1までの範囲しか無いので、
不定積分∫f(x)dt は、tの定義域が-1から1までに限定された関数です。
その不定積分∫f(x)dtを変数xで表した上の解の式のxの定義域は、tの値が-1から1までになる変数xの範囲です。
その変数x範囲は、マイナス無限大からプラス無限大まで使えます。
t=cos(x)の値が、-1から1までの範囲しか無いのに、
その範囲で積分される被積分関数をxで表した式が、
同じt=cos(x)を与えても、そのtに対応する変数xによる被積分関数sin(x)の値が2つありました。
その結果、-1から1の範囲で積分した不定積分をxで表した式が、同じtに対応しても、xの値が異なる毎に異なる不定積分の値を持つ、不定積分の関数が得られます。
すなわち、不定積分∫f(x)dx=∫f(g(t))g'(t)dtは、与えられた1つのtの値に対して、複数の値を持つ多価関数になっています。
これは、単純な、f(g(t))g'(t)のtによる不定積分の形とは異なった形の解です。
なぜなら、被積分関数f(x)=sinxをtによって積分する被積分関数に変換した関数f(g(t))g'(t)の値が1つのtの値に対して2つあるからです。そして、同じ値のtに対して、異なる値の被積分関数を使い分けて積分するからです。
【変数変換の不思議】
《微分不可能が微分可能に変わる例》
(注意1)関数の変数を変換すると微分不可能な点が微分可能な点に変わることがある。
下図のグラフの関数は、O点では傾きが無限大なのでxで微分不可能です。
(x=0を積分区間に含む関数f(x)の積分を置換積分する関数g(t)には、下図の関数は使えない事に注意)
しかし、変数xを以下のグラフの関係を持つ変数tに変換してみます。
この変数tで元の関数をあらわすと以下のグラフになります。
このグラフはO点で、tで微分可能です。
このように関数の変数を変換する、変数xでは微分不可能だった関数の点が、変数tでは微分可能になる、ということが起こり得ます。
という関係があります。
有限の微分係数が存在する(微分可能)という状態は、変数を変換すると変わることがあります。
それは、微分する変数に応じる「微分可能」という条件が、
いわば、
「式を0で割り算する計算をしてはいけない」
という計算の縛りと似た意味を持つことを意味しています。
(注意2)関数の変数を変換すると微分不可能な点が微分可能な点に変わることがあるもう1つの例を考える。
下図のグラフの関数は、O点では、左側微分係数と右側微分係数が異なるのでxで微分不可能です。
しかし、変数xを以下のグラフの関係を持つ変数tに変換してみます。
この変数tで元の関数をあらわすと以下のグラフになります。
このグラフはO点で、tで微分可能です。
このように関数の変数を変換すると、変数xでは微分不可能だった関数の点が、変数tでは微分可能になる、ということが起こり得ます。
(注意3)関数の変数を変換すると、接する2つグラフが接さない2つのグラフに変換される例を考える。
下の2つの関数のグラフは、O点で同じ微分係数=0を持ち、O点で接しています。
しかし、変数xを以下のグラフの関係を持つ変数tに変換してみます。
(この関数のグラフは、t=0の点での微分係数が無限大になってしまい、t=0では微分可能ではありません)
この変数tで元の2つの関数をあらわすと以下の2つのグラフになります。
元の2つのグラフの変数xを変数tに変換した2つのグラフは、O点で変数tで微分すると異なる微分係数を持ち、O点で接さず交差しています。
変数を変換すると、このように、互いに接する2つのグラフが、接触する点での微分係数が異なる2つのグラフに変わってしまうことがあることに気をつけましょう。
すなわち、「2つの接するグラフが接点において等しい微分係数を持つ」ことが、グラフの座標変換によって変わってしまい2つのグラフの接触点での微分係数が等しく無くなることが有り得ます。
その様なおかしな事が起こる場合は、変数のその値で微分可能では無い関数を使って変数を変換すると生じ得ます。おかしな事が起こらないようにする1つの十分条件として、変数変換に使う関数を、変数のその値で「微分可能」な関数を使えば、変数がその値の部分でのグラフにはおかしな事が起こりません。
「微分可能」は、このようにおかしな事が起こらないようにする十分条件なのです。これが、「微分可能」と「微分不可能」を区別する意味だと考えます。
(交差している2つのグラフが、変数変換すると互いに接する2つのグラフに変わる例)
上図のように、変数tの関数f(t)とg(t)との2つの関数値をY=f(t)、及びY=g(t)とする。
f(t)=t
g(t)=t/2
とする。 この場合に、上図のように、2つのグラフが、tY座標平面上では互いに交差しているだけで、接していない。
このグラフの変数tを以下のグラフの関数であらわす媒介変数xを考える。
変数tをこのグラフの関数であらわす媒介変数Xを使うと、
XY平面上で先の2つのグラフをあらわすと以下の図の様になる。
x≧0の場合に:
関数f(t)=x2
関数g(t)=x2/2
になる。
この様にXY座標平面上では、互いに接する2つのグラフに変換されてしまった。
すなわち、接さずに単に交差しているだけの2つのグラフが、互い接するグラフに変わってしまった。
(無難な変数変換の条件)
tY座標平面上の2つのグラフがある変数値において接するか否かを調べている時に、そのように関数の性質が変わってしまわない、変数tと媒介変数xの変数変換の条件は、その2つのグラフが交差する点の位置の変数値において:
dt/dx ≠ 0
となることが必要です。
また、その関数が”微分可能”であることも必要で、すなわち、その2つのグラフが交差する点の位置の変数値において:
dt/dx ≠ ±∞
も必要です。
この2つの条件を満足する関数で変数変換をするならば、グラフの所定の点での「微分可能」または「微分不可能」というグラフの性質が変数変換の後でも同じに維持されます。
例えば、log(X)という関数は、X=0以外の点では、この2つの条件を満足します。
そのため、この関数を使って変数変換するならば、X=0以外の点では、「微分可能」と「微分不可能」という性質が変わりません。
(関数の性質を変えない変数変換の使用例)
以下の式1であらわされるグラフを考えます。
Y=xa (式1) (定数 a は所定の実数)
この式1であらわされるグラフは、
グラフが滑らかである大部分の変数値xにおいて、
傾きが∞にならない点で、微分可能です。
この式1のグラフの微分可能性は、以下の様に変数変換して調べることもできます。
この式1を関数log(x)で変換すると、
log(Y)=a*log(X) (式2)
に変換されます。
この式2を
Z=log(Y) (Z>0)
t=log(X) (t>0)
で変数変換すると、
Z=a*t (式3) (ただし、Z>0,t>0)
が得られます。
この式3であらわされるグラフは、元の変数であらわされたグラフと、「微分可能」と「微分不可能」という性質が変わりません。
式3のグラフは「微分可能」ですので、元の式1であらわされたグラフも「微分可能」であることがわかります。
なお、置換積分法での解き方が違うと積分の解の式の形が違うことがあります。それは、同じ解の式が異なる形で表れているだけですので、異なる形であっても、その解を受け入れるべきです。
「(別ページ)形が違う同じ式」
【置換積分の条件はどこまで緩められるか】
置換積分の条件になっている、
「関数g(t)が微分可能であること」
という条件は、
「導関数g'(t)が積分可能であること」
という意味で設定された条件でした。
しかし、
g(t)がある1点で微分可能でなくても、
g(t)が1つながりに連続な関数であれば 、
その微分が出来ない1点は無視して、それ以外の関数値
f(g(t))g'(t)
を使って、
tで積分するならば、
不定積分の置換積分の公式:

が成り立つ。
なぜなら、リーマン積分によって関数を微小区間に分割して微小な面積の総和を取る積分の定義を、以下の図の様に変えた積分を定義できるからである。
上の図では、リーマン積分での微小区間の領域を、極限では同じ領域になる少し狭めた領域に変え、その領域の面積の極限を狭める前の微小区間の面積と同じにする。
その微小面積の総和を積分とする広義積分を使う。
こういうふうに微小領域を設定すれば、積分区間の端での関数値が何であるかを無視して積分することができる。
積分区間の端で関数が無限大に発散するような現象も、狭められた領域における、区間の端の近傍の関数値が無限大に発散する事で反映されるので、見逃される事が無い。
広義積分によれば、積分区間の端で媒介関数の微分g'(t)が存在しない場合でも積分ができる。
(広義積分の解答を書く場合には、良く説明する必要があります。ただし、高校数学では広義積分は扱わない。)
また、例えば、
x=g(t)=t, (t≦0)
x=g(t)=2t, (t≧0)
という、t=0では微分できない関数g(t)を使った場合。
g'(t)=1, (t<0)
g'(t)=2, (t>0)
であって、g'(t)は、t=0で連続ではありません。
しかし、g(t)は、t=0 で連続です。
また、t=0の点で(導関数g'(t)が定義されていない)そのtの値の近傍までg'(t)を積分して、その積分の極限値をt=0の点等での値g(0)と定義する広義積分をするならば、
そういう積分を定義して使うならば、
t=0では連続で無い導関数g'(t)を持つ媒介関数g(t)を使っても、
上の式であらわした不定積分の置換積分の公式の右辺の積分が、
t=0の点をまたいだ積分が可能になります。
広義積分によって積分可能になる条件として、以下の条件が考えられる。
「閉区間で積分可能で、かつ、最大値と最大値を持つ(有界であると言う)」関数同士の積の関数も積分可能な関数になります。 そのため、
「関数g(t)が、まばらにある微分不可能な点以外では、微分可能な関数であって、微分不可能な点でも連続で1つながりに連続な関数である」ならば、置換積分の公式が成り立ちます。
また、f(x)も「閉区間で積分可能で、かつ、最大値と最大値を持つ(有界であると言う)」条件が成り立つならば、f(x)が連続でなくても、置換積分の公式が成り立ちます。
結局、置換積分可能の条件を緩める限り緩めれば、以下の条件になる。
「閉区間[a,b]において、積分可能な関数f(x)に関して、
変数x=g(t)とおくとき、
g(t)は、まばらには存在し得る微分不可能な点を除外した点で微分可能であり、微分不可能な点でも連続な1つながりに連続な関数である事。
そして、
関数f(g(t))は、
「閉区間[a,b]で積分可能で、かつ、最大値と最大値を持つ(有界であると言う)」関数である事」
が、広義積分において置換積分の公式が成り立つための、(必要十分条件にかなり近い)十分条件です。
(これが必要条件では無い例の1つは、「変換された被積分関数の性質が変わる」にある積分です。その例でも、広義積分において、置換積分の公式が成り立つからです。)
この条件は、関数のイメージが湧き易い以下の条件に変えると覚え易いかもしれない。
「関数g(t)は、疎らには存在し得る微分不可能な点を除外した点で微分可能である、微分不可能な点でも連続な1つながりに連続な関数であり、
関数f(g(t))は、区間内で数点を除いて連続であり、
その数点でも無限大には発散しない(最大値と最小値を持つ有界な)関数であること」
リンク:
高校数学の目次







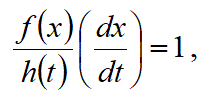
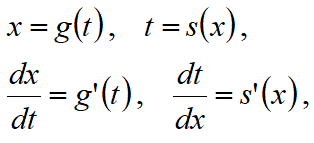
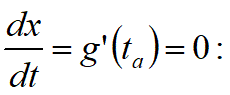



































































0 件のコメント:
コメントを投稿