【問】座標の回転変換の公式を複素数平面で導け。
以下の図のように、ベクトル（Ｘ，Ｙ）を、左回りに角度θ回転させたベクトル（Ｘ’，Ｙ’）の各座標を、ＸとＹであらわす座標の回転変換の公式を導け。
上の式で、ベクトル（Ｘ，Ｙ）を、左回りに角度θ回転させたベクト（Ｘ’，Ｙ’）の座標をあらわすベクトルの回転変換の公式が得られた。
ここで、
（ｘ，ｙ）を（ｘ’，ｙ’）であらわす式と、
（ｘ’，ｙ’）を（ｘ，ｙ）であらわす式とは、
以下の式の様に、θの正負を逆にしただけの式であらわされる、
回転変換式の間の対の関係がありますので、覚えておきましょう。
この回転変換の公式は常識として、素早く導き出せるようにしましょう。
この回転変換の公式は、図を目の視線でたどって、以下の様に場合分けした式の部分を素早く導き出せるようになりましょう。
すなわち、
上の図を思い描いて、図から、
Ｘ座標のみがある場合のＹ’座標が（ｓｉｎθ）・Ｘであること。
Ｙ座標のみがある場合のＸ’座標が（－ｓｉｎθ）・Ｙであること。
を想像します。
次に、それ以外は、係数がｃｏｓθの項を加えることで、
下式の回転変換の式ができあがります。
また、計算式は、以下のように視線を動かして、速く計算できるようになりましょう。
リンク：
複素数平面での座標回転を応用した例
ベクトルの外積が複素数の積で表わせる関係を初めて学ぶときは、
以下のように考えてこの関係があることを納得して学ぶ事が望ましいです。
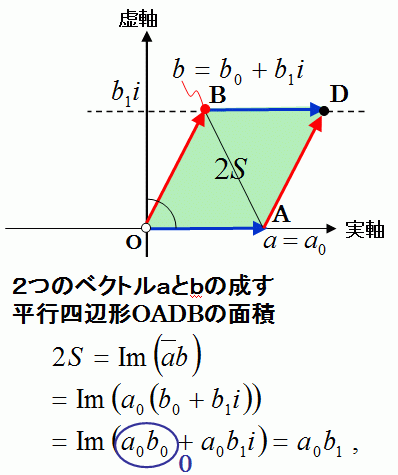
【問１】
下図のような、複素数平面上のベクトルａとｂで作られる平行四辺形（長方形）の面積２Ｓを計算せよ。
面積２Ｓは、上の式であらわせます。
【問２】
下図のような、左に９０度回転したベクトルａとｂで作られる平行四辺形（長方形）の面積２Ｓを計算せよ。
面積２Ｓは、上の式であらわせます。
【問３】
下図のような、複素数平面上のベクトルａと、実軸方向に平行に傾けたベクトルｂで作られる平行四辺形（長方形）の面積２Ｓを計算せよ。
面積２Ｓは、上の式であらわせました。
【問４】
下図のような、複素数平面上のベクトルｂと、虚軸方向に平行に傾けたベクトルａで作られる平行四辺形（長方形）の面積２Ｓを計算せよ。
面積２Ｓは、上の式であらわせました。
【問５】
下図のような、ベクトルａとｂで作られる平行四辺形（長方形）の面積２Ｓを計算せよ。
この式は、個別に成分に分解した以下の式で計算することができます。
この計算は、以下の図形の面積の変形操作と解釈できます。
この面積の式は、以下の様に、まとまった複素数同士の積の計算の結果の一部であると解釈することができます。
この式の実数成分は、以下のようにベクトルの内積をあらわし、
虚数成分は、以下のようにベクトルの作る平行四辺形の面積をあらわします。
ここで、２つのベクトルの成す平行四辺形ＤＢＯＡの面積をベクトルの掛け算（×）であらわし、ベクトルの外積と呼びます。
（注意）
ベクトルの外積の定義を厳密に言うと、
「２つのベクトルどちらにも垂直な方向（この図の場合は紙面に垂直な方向）のベクトルを計算すること。そのベクトルの長さは、平行四辺形ＤＢＯＡの面積にする。」
です。
リンク：
第２講４節 点と直線の距離（三角形の面積）
追加講 三角形の面積と行列式
高校数学の目次
べクトルの外積を複素数を使って計算する
複素数平面であらわした複素数はベクトルです。
ベクトルの外積は平行四辺形の面積の値を与えます。
複素数平面上の複素数を用いても素早くベクトルの外積（平行四辺形の面積）を計算できるようになりましょう。
【問】
平行四辺形の面積を複素数平面で計算するにはどうすれば良いか？
その解を考えると、以下の式が考え出せます。
以降で、この式が実際の計算問題を解くためにどれだけ使える式なのか、調べてみます。
リンク：
高校数学の目次
以下に、ベクトルの内積の計算を複素数で表現します。
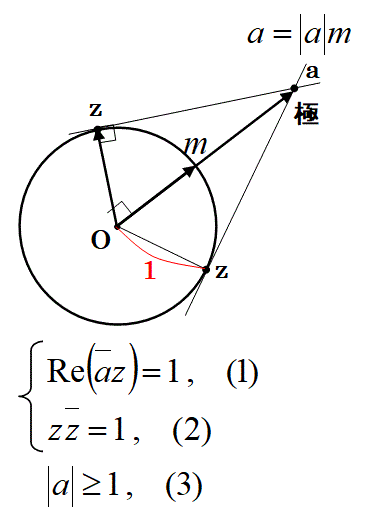
【問】複素数平面上の原点Ｏを中心にする半径１の円（ｘ２＋ｙ２＝１）に対して、複素数であらわした点ａから引いた２つの接線の円との接点ｂとｃの位置を複素数であらわせ。
この問題は、ベクトルの内積を使って答えを計算する問題ですが、そのベクトルを複素数で表わして答えを計算する複素数の記号の使い方と内積の式の表現方法を以下で説明します。
以下の説明を見れば分かるように、ベクトル記号の→記号を毎回符号の上に追加して書くわずらわしさから解放されるので、複素数を使ってベクトルを表現した計算は、その式を書くのがとても楽になります。
（解）
先ず、この問題の円の中心Ｏから点ａまでの単位ベクトルｍを考えます。
先ず、この問題をもっと易しい問題に変換して解きます。
【問１】以下の点ａから引いた２つの接線の円との接点ｂとｃの位置ベクトルを求めよ。
このように簡単化した問題は、すぐ上の式であらわしたベクトルとしての複素数ｍが点ｂとｃをあらわす解があります。
もう１つのやさしい問題を解きます。
【問２】以下の点ａから引いた２つの接線の円との接点ｂとｃの位置ベクトルを求めよ。
このようにベクトルとしての複素数ａの長さが無限大の場合では、点ｂの複素数ｂは、値０を掛け算したベクトルとしての複素数ｍと、それに垂直なベクトルとしての複素数ｐの和の解になると解釈します。
もう１つのやさしい問題を解きます。
【問３】以下の点ａから引いた２つの接線の円との接点ｂとｃの位置ベクトルを求めよ。
このようにベクトルａの長さが√２の場合では、ベクトルとしての複素数ｂは、１／√２を掛け算したベクトルｍと、それに垂直なベクトルｐの何倍かの和の解になると解釈します。
次に、以上で得られた解から、一般的な解を以下のように推測します。
上の式のように、ベクトルとしての複素数ｂの公式をハッキリした式で推測しました。
また、この推測の結果は、この公式を導き出すための基準にするベクトルはベクトルｍとそれに垂直なベクトルｐを基準にしたら良いと示唆するという重要な指針（計算のガイド）を含んでいます。
これで得た公式は推測であって、本当にこの式になるかの確証があるわけではありません。
しかし、これで、公式の答えを予測できたので、正式な計算で公式を計算する道しるべができたという意味があります。
このように、答えを予測する計算は、初めて未知の問題を解くときに大切な一歩であり、必要な計算です。是非、答えの予測計算を心がけて欲しいと思います。
次に、正式な計算方法でこの公式を求めます。
【一番簡単な解き方の秘訣】
（あるベクトルｂとベクトルＡＢとが互いに垂直であるという条件のある図形の問題を解くときは、
（１）それらのベクトルｂとＡＢを、互いに垂直な単位ベクトルｍとｐの合成であらわして、
（２）そして、ベクトルｂとＡＢが垂直である条件として内積が０であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。）
以下の図のような図を考えて、ベクトル方程式を解いてベクトルｂをあらわす公式を計算します。
ここで、ベクトルとしての複素数ｂを、
互いに直交するベクトルｍとｐを用いてあらわし、
それらのベクトルが実数の未知数ｓ倍とｔ倍されて合成されたものとしてあらわす。
そして、ベクトルｂとベクトルＡＢが直交する以下のベクトル方程式を作って、それらの未知数ｓとｔを求めます。
このベクトルとしての複素数ｂの式の形を整えるにあたって、先に予測した式になっているかを確かめながら、予測した式になるように式を変形しました。
その結果、予測通りの式が得られました。
この結果を使って、ベクトルｂが以下の図のようにあらわせます。
（計算を振り返ってどこが良かったかを考える）
以上の計算で大事なポイントは、先に公式の解の形を予測してから正式な計算に取りかかった事でした。答えを予測してから正式な計算をしたことで、正式な計算が、「本当に予測通りの答えを導き出せるのか」という期待に背中を押されて計算できました。
そして、式を計算していく過程で、どういう形の式に答えを導くべきかの目標がはっきりしているので、式を何に置き換えてまとめ上げるかの道に迷わず、答えを得ることができました。
すなわち、先に予測していた事が、式を次にどのような形に変形したら良いかというガイドになりました。
このガイドが無ければ、式の計算が最後の形にまで変形できなかったかもしれませんので、先に行なった解の推測の計算がとても大切な役割を果たしました。
特に、先に行なった解の推測の計算は、問題を解くために、どのベクトルを基準にしたら良いかを示唆するという重要な指針を含んでいますので、問題を解くためにとても大切な役割を持っていました。
【解２】
以下の様に解くこともできます。
（ｂとｃの解答おわり）
リンク：
高校数学の目次
また、計算式は、以下のように視線を動かして、速く計算できるようになりましょう。
