曲線と直線が接する問題の簡単な解き方。
それは、円への接線を求める問題の場合には、ベクトルを使って接線を表現して考える方が、連立方程式の交点が重解を持つことで接線を表現して解くよりも、問題が簡単に解けます。
【問１】座標原点を中心にする半径１の円（ｘ２＋ｙ２＝１）と、直線３ｘ＋２ｙ＝ｋとが接する場合のｋの値を求めよ。
（予備知識）
難しい形の図形は、その座標を単純な形の基本的な座標での図形に置きかえて考えます。
（難しい形の図形は、全て、単純な座標での図形に置き換えて考えるのが数学のコツです。）
【解答開始】
（まず、問題を単純化する）
円の式は以下の式１で与えられました。
ｘ２＋ｙ２＝１ （式１）
直線の式は以下の式２です。
３ｘ＋２ｙ＝ｋ （式２）
ここで、この直線の式（式２）は、もっと基本的な形をした単純な意味を持つ式に書きかえられます。
式２のｘとｙの係数はベクトル（３，２）を成します。
このベクトルを、長さが１の単位ベクトルに変換します。
その変換は、ベクトル（３，２）を
で割り算すれば、単位ベクトルに変わります。
検算してみると、
になるので、このベクトルが単位ベクトルであることがわかります。
直線をあらわす（式２）を
で割り算すれば、ｘとｙの係数が単位ベクトルであらわされた直線の式になります。
その直線の式において、（単位ベクトル）と（ベクトル（ｘ，ｙ））との内積は、その直線の座標原点からの距離をあらわします。
（その理由は単位ベクトルと直線上の点（ｘ，ｙ）の位置ベクトルの内積は、直線上の点のその単位ベクトル（直線に垂直）への正射影の長さになるからです。また、直線に垂直な単位ベクトルへの、座標原点と点（ｘ，ｙ）を結ぶベクトルの正射影の長さは、直線と座標原点との距離だからです。）
すなわち、単位ベクトルと直線上の点（ｘ，ｙ）の位置ベクトルの内積をあらわす左辺の式に等しい右辺の式の、
が、直線の座標原点からの距離です。
この距離が式１の円の半径１になれば、この直線が円に接します。
よって、もとめるｋの値は、
の場合に、直線が円に接します。上の式を変形すると、
これが直線が円に接する場合のｋの値です。
以上の解答方法によれば、求める解をもらさず網羅的に求めています。
（解答おわり）
---（接点Cを通る直線の公式）----
ｋを調整して直線を円に接するようにすると、例えば、
ｋ＝√(13)にすれば、
その直線の接点は上図のC点になります。
そのとき、式２は以下の式２’になります。
式２’を上の計算の様に式３に変形すると、
式３は、式３’の様に、接点Cの座標を使って表した式になります。
これはいつも成り立ち、
式１の円の接点Cを通る直線は、式３’で表されます。
===（その理由）==========
なぜなら、式３’の左辺は、円の中心を原点にした場合の、点Cの位置ベクトルと、
そのベクトルへ直線上の点（ｘ，ｙ）の位置ベクトルを正射影したベクトル、
との積をあらわします。
それにより以下の２つが成り立つからです。
（１）
点Ｃが接点の場合は正射影したベクトルの先端は点Ｃになります。
（２）
直線の係数が作るベクトルＣは、直線に垂直なベクトルです。そのため、ベクトルＣに直線上の点（ｘ，ｙ）を正射影したベクトルの先端の位置が円上にあれば、直線が円に接します。
====================
また、半径ｒ円の式が以下の式１ａで表される場合：
ｘ２＋ｙ２＝ｒ２ （式１ａ）
この円の接点Ｃを通る接線の式は：
であらわされます。
--（接点Cを通る直線の公式おわり）-----
（ベクトルで考えると計算が整理できる）
上の解答では、ベクトルの内積の知識を使って問題を解きました。
以下では、ベクトルを使って考えますが、以下のようにして、内積の知識の使い方を控え目にして問題を解けます。
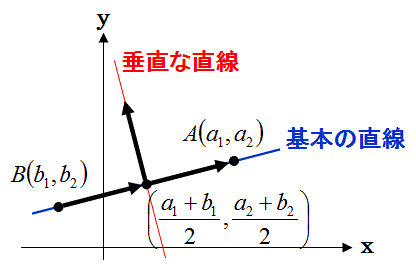
直線の式は、ベクトルから考えると以下の意味を持ちます。
直線の式の直線上の座標ｘの微小変化量にｘの係数を掛け算した値と座標ｙの微小変化量にｙの係数を掛け算した値は０になります。
ベクトルの視点で見ると、そのように積の和（この積の和を内積と呼びます）が０になる場合は、ｘの係数とｙの係数で与えられる点Ｃと座標原点Ｏを通る直線は、その式で与えられた直線と直交することがわかっています。
このベクトルの視点から分かる知識だけを加えて考えるだけで、この問題を完全に解くことができます。
すなわち、連立方程式：
において、式２を以下の式３に変形して：
この式の未知数ｘ、ｙ、ｋを以下の値に当てはめる。
この式４、５、６で未知数ｘ、ｙ、ｋの値を定めると、
式３は以下の式７になる。
この式７は、式１の未知数ｘ、ｙを式４と式５の値に当てはめた式１になった。
すなわち、式６で未知数ｋを定めた直線３上の点の座標を与える式４と式５の座標点Ｃ（ｘ，ｙ）が式１を満足した。
ゆえに、点Ｃ（ｘ，ｙ）は、式１で与えられる円周にある。
式６で未知数ｋを定めた直線３と円１はこの座標点Ｃ（ｘ，ｙ）で交わる。
次に、考慮することは、ベクトルの視点で見た直線２の式は、直線ＯＣに垂直であることである。
このことを考えると、式６で未知数ｋを定めた直線３は、円と交わる点Ｃを通るだけでなく、円の半径ＯＣに垂直であり、点Ｃで円に交わることがわかる。
式６でｋの値を定めると、直線２は円１と点Ｃで接する。
最後に考慮すべきことは、以上の解き方では、問題の解を網羅的に求めてはいないので、以上の解がこの問題の解の全てであるかということを確認する必要があります。
実際、もう１組の解として、以下の式８、９、１０で未知数ｘ，ｙ，ｋを定めることができます。
（解答おわり）
このように、ベクトルの視点を加えて考えることで、直線の式２の持つ図形的意味を明瞭に把握しながら問題が解けるので、問題を解くために、とても助かります。
リンク：
高校数学の目次
それは、円への接線を求める問題の場合には、ベクトルを使って接線を表現して考える方が、連立方程式の交点が重解を持つことで接線を表現して解くよりも、問題が簡単に解けます。
【問１】座標原点を中心にする半径１の円（ｘ２＋ｙ２＝１）と、直線３ｘ＋２ｙ＝ｋとが接する場合のｋの値を求めよ。
（予備知識）
難しい形の図形は、その座標を単純な形の基本的な座標での図形に置きかえて考えます。
（難しい形の図形は、全て、単純な座標での図形に置き換えて考えるのが数学のコツです。）
【解答開始】
（まず、問題を単純化する）
円の式は以下の式１で与えられました。
ｘ２＋ｙ２＝１ （式１）
直線の式は以下の式２です。
３ｘ＋２ｙ＝ｋ （式２）
ここで、この直線の式（式２）は、もっと基本的な形をした単純な意味を持つ式に書きかえられます。
式２のｘとｙの係数はベクトル（３，２）を成します。
このベクトルを、長さが１の単位ベクトルに変換します。
検算してみると、
その直線の式において、（単位ベクトル）と（ベクトル（ｘ，ｙ））との内積は、その直線の座標原点からの距離をあらわします。
（その理由は単位ベクトルと直線上の点（ｘ，ｙ）の位置ベクトルの内積は、直線上の点のその単位ベクトル（直線に垂直）への正射影の長さになるからです。また、直線に垂直な単位ベクトルへの、座標原点と点（ｘ，ｙ）を結ぶベクトルの正射影の長さは、直線と座標原点との距離だからです。）
すなわち、単位ベクトルと直線上の点（ｘ，ｙ）の位置ベクトルの内積をあらわす左辺の式に等しい右辺の式の、
この距離が式１の円の半径１になれば、この直線が円に接します。
よって、もとめるｋの値は、
以上の解答方法によれば、求める解をもらさず網羅的に求めています。
（解答おわり）
---（接点Cを通る直線の公式）----
ｋを調整して直線を円に接するようにすると、例えば、
ｋ＝√(13)にすれば、
その直線の接点は上図のC点になります。
そのとき、式２は以下の式２’になります。
式３は、式３’の様に、接点Cの座標を使って表した式になります。
これはいつも成り立ち、
式１の円の接点Cを通る直線は、式３’で表されます。
===（その理由）==========
なぜなら、式３’の左辺は、円の中心を原点にした場合の、点Cの位置ベクトルと、
そのベクトルへ直線上の点（ｘ，ｙ）の位置ベクトルを正射影したベクトル、
との積をあらわします。
それにより以下の２つが成り立つからです。
（１）
点Ｃが接点の場合は正射影したベクトルの先端は点Ｃになります。
（２）
直線の係数が作るベクトルＣは、直線に垂直なベクトルです。そのため、ベクトルＣに直線上の点（ｘ，ｙ）を正射影したベクトルの先端の位置が円上にあれば、直線が円に接します。
====================
また、半径ｒ円の式が以下の式１ａで表される場合：
ｘ２＋ｙ２＝ｒ２ （式１ａ）
この円の接点Ｃを通る接線の式は：
--（接点Cを通る直線の公式おわり）-----
（ベクトルで考えると計算が整理できる）
上の解答では、ベクトルの内積の知識を使って問題を解きました。
以下では、ベクトルを使って考えますが、以下のようにして、内積の知識の使い方を控え目にして問題を解けます。
ベクトルの視点で見ると、そのように積の和（この積の和を内積と呼びます）が０になる場合は、ｘの係数とｙの係数で与えられる点Ｃと座標原点Ｏを通る直線は、その式で与えられた直線と直交することがわかっています。
このベクトルの視点から分かる知識だけを加えて考えるだけで、この問題を完全に解くことができます。
すなわち、連立方程式：
式３は以下の式７になる。
すなわち、式６で未知数ｋを定めた直線３上の点の座標を与える式４と式５の座標点Ｃ（ｘ，ｙ）が式１を満足した。
ゆえに、点Ｃ（ｘ，ｙ）は、式１で与えられる円周にある。
式６で未知数ｋを定めた直線３と円１はこの座標点Ｃ（ｘ，ｙ）で交わる。
次に、考慮することは、ベクトルの視点で見た直線２の式は、直線ＯＣに垂直であることである。
このことを考えると、式６で未知数ｋを定めた直線３は、円と交わる点Ｃを通るだけでなく、円の半径ＯＣに垂直であり、点Ｃで円に交わることがわかる。
式６でｋの値を定めると、直線２は円１と点Ｃで接する。
最後に考慮すべきことは、以上の解き方では、問題の解を網羅的に求めてはいないので、以上の解がこの問題の解の全てであるかということを確認する必要があります。
実際、もう１組の解として、以下の式８、９、１０で未知数ｘ，ｙ，ｋを定めることができます。
このように、ベクトルの視点を加えて考えることで、直線の式２の持つ図形的意味を明瞭に把握しながら問題が解けるので、問題を解くために、とても助かります。
リンク：
高校数学の目次
